Ciri amplitud gelombang, formula dan senaman

The Amplitud gelombang Ia adalah anjakan maksimum yang dialami oleh titik dalam gelombang berkenaan dengan kedudukan keseimbangan. Gelombang itu nyata di mana -mana dan banyak cara di dunia di sekeliling kita: di lautan, dalam bunyi dan dalam tali alat yang menghasilkannya, dalam cahaya, di permukaan bumi dan banyak lagi.

Salah satu cara untuk menghasilkan gelombang dan mengkaji kelakuannya adalah memerhatikan getaran tali yang mempunyai hujung tetap. Dengan menghasilkan gangguan di hujung yang lain, setiap zarah tali berayun dan dengan itu tenaga gangguan itu dihantar dalam bentuk penggantian denyutan sepanjang.

Gelombang nyata dalam pelbagai cara. Sumber: Pixabay.

Apabila tenaga merebak, tali yang sepatutnya menjadi elastik sempurna, mengamalkan bentuk sinusoidal biasa dengan rabung dan lembah yang ditunjukkan dalam angka yang muncul di bawah di bahagian berikut.

[TOC]

Ciri dan makna amplitud gelombang

Amplitud A adalah jarak antara puncak dan paksi rujukan atau tahap 0. Sekiranya disukai, antara lembah dan paksi rujukan. Sekiranya gangguan dalam tali adalah ringan, amplitud A kecil. Sekiranya sebaliknya gangguannya sengit, amplitud akan lebih besar.

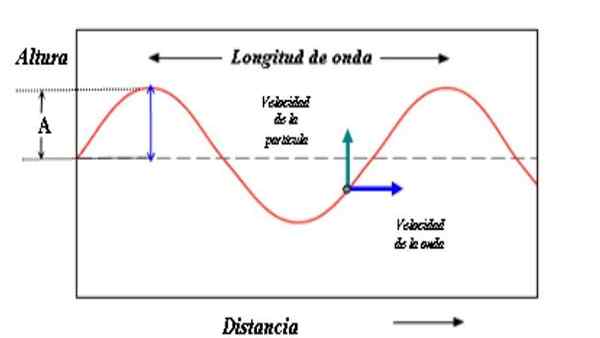Model untuk menggambarkan gelombang terdiri daripada lengkung sinusoidal. Amplitud gelombang adalah jarak antara puncak atau lembah dan paksi rujukan. Sumber: PACO [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Nilai amplitud juga merupakan ukuran tenaga yang memakai gelombang. Intuitif amplitud yang hebat dikaitkan dengan tenaga yang lebih besar.

Sebenarnya tenaga adalah berkadar dengan kuadrat amplitud, yang menyatakan secara matematik adalah:

I ∝A²

Boleh melayani anda: induktansi bersama: formula/pekali, aplikasi, latihan

Di mana saya adalah intensiti gelombang, pada gilirannya berkaitan dengan tenaga.

Jenis gelombang yang dihasilkan dalam tali contoh, tergolong dalam kategori gelombang mekanikal. Ciri penting ialah setiap zarah di tali selalu sangat dekat dengan kedudukan keseimbangannya.

Zarah tidak bergerak atau bergerak melalui tali. Mereka naik dan turun. Ini ditunjukkan dalam skim teratas dengan anak panah hijau, namun gelombang bersama dengan tenaganya, bergerak dari kiri ke kanan (anak panah biru).

Gelombang yang tersebar di dalam air memberikan bukti yang diperlukan untuk meyakinkan diri mereka mengenai perkara ini. Memerhatikan pergerakan lembaran yang telah jatuh ke dalam kolam yang dapat dilihat bahawa dia hanya berayun yang mengiringi pergerakan air. Ia tidak jauh, sekurang -kurangnya jelas, bahawa ada kekuatan lain yang menyediakan pergerakan lain.

Model gelombang yang ditunjukkan dalam angka terdiri daripada corak berulang di mana jarak antara dua rabung adalah panjang gelombang λ. Sekiranya anda mahu, panjang gelombang juga memisahkan dua mata yang sama dari gelombang, walaupun ketika mereka tidak berada di puncak.

Penerangan matematik gelombang

Sememangnya, gelombang dapat digambarkan oleh fungsi matematik. Fungsi berkala seperti sinus dan kosinus adalah ideal untuk tugas, sama ada anda ingin mewakili gelombang di ruang angkasa dan dalam masa.

Jika kita memanggil paksi menegak dalam angka dan paksi mendatar yang kita sebut "t", maka tingkah laku gelombang dari masa ke masa dinyatakan oleh:

y = cos (ωt + δ)

Untuk pergerakan ideal ini, setiap zarah tali berayun dengan pergerakan harmonik yang mudah, yang berasal terima kasih kepada daya yang berkadar terus dengan anjakan yang dibuat oleh zarah.

Boleh melayani anda: Model Atom Dirac Jordan: Ciri -ciri dan Postulates

Dalam persamaan yang dicadangkan, a, Ω dan δ adalah parameter yang menggambarkan pergerakan, ke arah amplitud sebelum ini ditakrifkan sebagai anjakan maksimum yang dialami oleh zarah berkenaan dengan paksi rujukan.

Hujah kosinus dipanggil Fasa pergerakan Dan δ adalah pemalar fasa, Apakah fasa ketika t = 0. Kedua -dua fungsi kosinus dan fungsi sinus sesuai untuk menggambarkan gelombang, kerana mereka hanya berbeza antara satu sama lain π/2.

Biasanya mungkin untuk memilih t = 0 dengan δ = 0 untuk mempermudah ungkapan, mendapatkan:

y = cos (ωt)

Apabila pergerakan berulang -ulang di ruang dan masa, ada masa ciri yang merupakan tempoh t, ditakrifkan sebagai masa yang diperlukan untuk zarah untuk melaksanakan ayunan lengkap.

Penerangan Gelombang Dalam Masa: Parameter Ciri

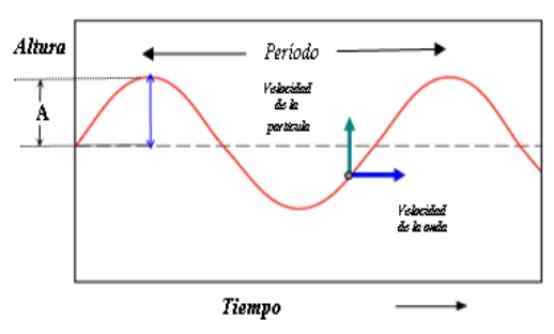Angka ini menunjukkan keterangan gelombang dalam masa. Jarak antara rabung (atau lembah) kini sesuai dengan tempoh gelombang. Sumber: PACO [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Sekarang, kedua -dua payudara dan kosinus mengulangi nilainya apabila fasa meningkat dalam nilai 2π, supaya:

ωt = 2π → Ω = 2π /t

Ω dipanggil kekerapan pergerakan sudut Dan ia mempunyai dimensi masa terbalik, sebagai unitnya dalam sistem antarabangsa radián / kedua atau kedua^-1.

Akhirnya anda boleh menentukan Kekerapan pergerakan F, sebagai songsang atau timbal balik tempoh. Mewakili bilangan rabung per unit masa, dalam hal ini:

F = 1/t

Ω = 2πf

Kedua -dua f dan Ω mempunyai dimensi dan unit yang sama. Sebagai tambahan kepada yang kedua^-1, yang dipanggil hertz atau hertzio, adalah perkara biasa untuk didengar Revolusi sesaat Sama ada Revolusi seminit.

Kelajuan gelombang v, Yang mesti ditekankan bahawa ia tidak sama seperti yang dialami oleh zarah, ia dapat dengan mudah dikira jika panjang gelombang λ dan kekerapan f diketahui:

Ia dapat melayani anda: badan bercahaya: ciri -ciri dan bagaimana mereka menjana cahaya mereka sendiri

V = λf

Jika ayunan yang dialami oleh zarah adalah jenis harmonik yang mudah, kekerapan sudut dan kekerapan hanya bergantung pada sifat zarah berayun dan ciri -ciri sistem. Amplitud gelombang tidak menjejaskan parameter ini.

Sebagai contoh, ketika memainkan nota muzik pada gitar, nota itu akan selalu mempunyai nada yang sama walaupun ia disentuh dengan intensiti yang lebih besar atau lebih rendah, dengan cara ini akan selalu terdengar seperti yang dilakukan, walaupun didengar lebih kuat atau lebih lembut komposisi, sama ada di piano atau gitar.

Secara semula jadi, gelombang yang diangkut dalam persekitaran material di semua arah dilemahkan kerana tenaga hilang. Atas sebab ini amplitud berkurang dengan kebalikan dari jarak r kepada sumber, mungkin untuk mengesahkan bahawa:

A∝1/r

Latihan diselesaikan

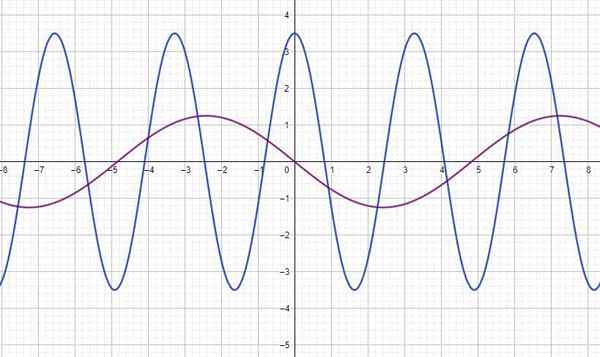
Angka ini menunjukkan fungsi y (t) untuk dua gelombang, di mana dan dalam meter dan t dalam beberapa saat. Untuk setiap orang dapati:

a) amplitud

b) Tempoh

c) kekerapan

d) Persamaan setiap gelombang dari segi payudara atau cosenos.

Jawapan

a) Ia diukur secara langsung dari graf, dengan bantuan grid: gelombang biru: a = 3.5m; Gelombang Fuchsia: A = 1.25 m

b) Ia juga membaca graf, menentukan pemisahan antara dua puncak atau lembah, berturut -turut: gelombang biru: t = 3.3 saat; Fuchsia Wave T = 9.7 saat

c) Ia dikira mengingati bahawa kekerapan adalah timbal balik tempoh: Gelombang biru: f = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

d) Gelombang biru: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia Wave: Y (T) = 1.25 dosa (0.65t) = 1.25 cos (0.65T+1.57)

Perhatikan bahawa gelombang fuchsia sudah ketinggalan zaman π/2 berkenaan dengan biru, yang mungkin mewakilinya dengan fungsi sinus. Atau cosine yang dipindahkan π/2.