Definisi rig faktorial, formula dan latihan

Dia Rig faktorial Ia adalah mesin mudah yang terdiri daripada susunan takal dengan kesan pengganda kekerasan. Dengan cara ini, anda boleh menaikkan beban yang memohon hanya setara dengan sebahagian kecil daripada berat pada akhir tali.

Ia terdiri daripada dua set pulleys: satu yang ditetapkan untuk sokongan dan yang lain yang menghasilkan daya yang dihasilkan pada beban. Kendi dipasang pada bingkai logam umum yang memegangnya. 

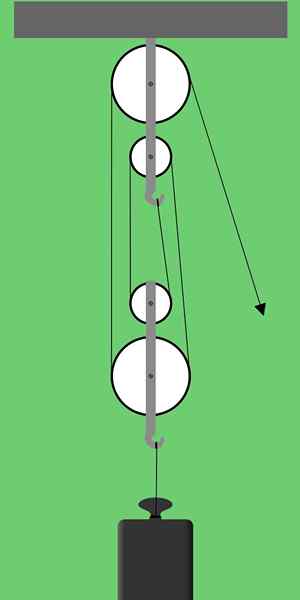
Rajah 1. Skim pelantar faktorial. Sumber: Pixabay

Rajah 1 menunjukkan rig faktorial yang terdiri daripada dua kumpulan dua kendi masing -masing. Pengaturan pulley jenis ini juga dipanggil Rig Siri Sama ada Polypasts.

[TOC]

Formula Factorial Right

Kes 1: Pulley Mudah Alih dan Tetap

Untuk memahami mengapa pengaturan ini melipatgandakan daya yang dikenakan, kita akan bermula dengan kes yang paling mudah, yang terdiri daripada pulley tetap dan mudah alih.

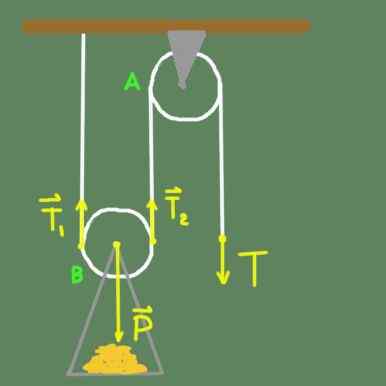Rajah 2. Dua Rig Pulley.

Dalam Rajah 2 kita mempunyai takal tetap ke bumbung dengan sokongan. Pulley A boleh berputar dengan bebas di sekitar paksi. Kami juga mempunyai pulley b yang mempunyai sokongan tetap pada paksi pulley, di mana beban diletakkan. Pulley B, selain dapat berputar secara bebas di sekitar paksi, mempunyai kemungkinan untuk bergerak secara menegak.

Katakan kita berada dalam keadaan seimbang. Pertimbangkan kekuatan yang bertindak pada pulley b. Paksi b -pulley menyokong jumlah berat p yang diarahkan ke bawah. Jika ini adalah satu -satunya daya pada pulley B maka, tetapi kita tahu bahawa tali yang melewati takal ini juga mengerahkan dua daya, iaitu T1 dan T2 yang diarahkan ke atas.

Agar keseimbangan translasi, kedua -dua daya mestilah sama dengan berat badan yang menyokong paksi pulley b.

T1 + t2 = p

Tetapi sejak pulley b juga dalam keseimbangan putaran, maka t1 = t2. Daya T1 dan T2 datang dari ketegangan yang digunakan pada tali, yang dipanggil t.

Ia dapat melayani anda: model atom bohr

Oleh itu t1 = t2 = t. Menggantikan persamaan sebelumnya kekal:

T + t = p

2t = p

Menunjukkan bahawa ketegangan yang digunakan pada tali hanya separuh berat:

T = p/2

Contohnya, jika bebannya 100 kg sudah cukup untuk memohon daya 50 kg di hujung bebas tali untuk menaikkan beban pada kelajuan malar.

Kes 2: Dua Mudah Alih dan Dua Pulley Tetap

Mari kita pertimbangkan ketegangan dan daya yang bertindak pada satu set yang terdiri daripada dua sokongan sokongan A dan B dengan dua kendi masing -masing.

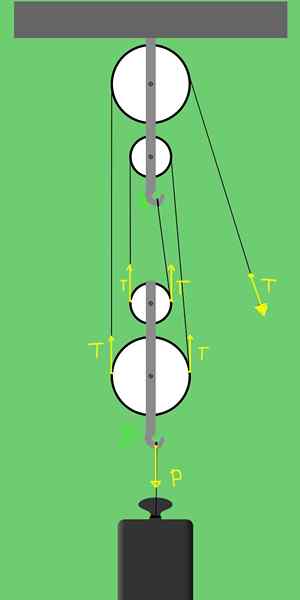Rajah 3. Kuasa pada rig 2 kendi tetap dan 2 kendi mudah alih.

Sokongan B mempunyai kemungkinan bergerak secara menegak, dan pasukan yang bertindak pada anak lelaki:

- Berat p beban, yang menunjuk secara menegak.

- Dua ketegangan pada takal besar dan dua ketegangan pada takal kecil. Secara keseluruhan, empat ketegangan, semuanya menunjuk.

Kerana ada keseimbangan translasi, adalah perlu bahawa daya yang menunjuk secara menegak ke atas sama dengan beban yang menunjuk ke bawah. Iaitu, ia mesti dipenuhi:

T + t + t + t = p

Iaitu, 4 t = p

Dari mana ia mengikuti bahawa daya yang digunakan T di hujung bebas tali hanya seperempat berat kerana beban yang ingin bangkit., T = p / 4.

Dengan nilai ini untuk voltan T, beban dapat dikekalkan statik atau meningkat dengan kelajuan tetap. Sekiranya voltan yang lebih besar digunakan daripada nilai ini maka beban akan mempercepatkan, syarat yang diperlukan untuk mengeluarkannya dari yang lain.

Kes Umum: N Pulleys Mobile dan N Pulleys Tetap

Seperti yang dilihat dalam kes -kes sebelumnya, bagi setiap pulley set mudah alih terdapat beberapa daya ke atas dengan tali yang melewati takal. Tetapi daya ini tidak boleh menjadi apa -apa selain ketegangan yang digunakan pada tali di hujung bebas.

Oleh itu, bagi setiap pulley set mudah alih akan ada daya ke atas yang bernilai 2T. Tetapi kerana terdapat n pulleys dalam set mudah alih, kemudian perlu untuk menunjukkan secara menegak ke atas adalah:

Boleh melayani anda: Enjin sangkar tupai

2 n t

Untuk keseimbangan menegak, perlu:

2 n t = p

Oleh itu daya yang digunakan pada akhir percuma adalah:

T = p / (2 n)

Dalam kes ini, dapat dikatakan bahawa kekuatan yang dikenakan t melipatgandakan 2 kali pada beban.

Sebagai contoh, jika kita mempunyai rig faktorial 3 pulley tetap dan 3 telefon bimbit, nombor N akan sama dengan 3. Sebaliknya, jika beban adalah p = 120 kg, maka daya yang digunakan pada akhir bebas ialah t = 120 kg / (2*3) = 20 kg.

Latihan yang diselesaikan

Latihan 1

Pertimbangkan rig faktorial yang terdiri daripada dua kapi tetap dan dua kapi mudah alih. Ketegangan maksimum yang dapat menyokong tali adalah 60 kg. Tentukan apakah beban maksimum yang boleh diletakkan.

Penyelesaian

Apabila beban berehat atau bergerak sentiasa berat p daripadanya, ia berkaitan dengan ketegangan t yang digunakan dalam tali melalui hubungan berikut:

P = 2 n t

Kerana ia adalah rig dua mudah alih dan dua kendi tetap, kemudian n = 2.

Beban maksimum yang boleh diletakkan diperoleh apabila t mempunyai nilai maksimum yang mungkin, yang dalam kes ini adalah 60 kg.

Beban maksimum = 2*2*60 kg = 240 kg

Latihan 2

Cari hubungan antara ketegangan tali dan berat beban, dalam rig faktorial dua kendi di mana beban dipercepat dengan pecutan ke.

Penyelesaian

Perbezaan dalam contoh ini berkenaan dengan apa yang telah dilihat setakat ini ialah dinamik sistem mesti dipertimbangkan. Oleh itu, kami mencadangkan undang -undang kedua Newton untuk mencari hubungan yang diminta.

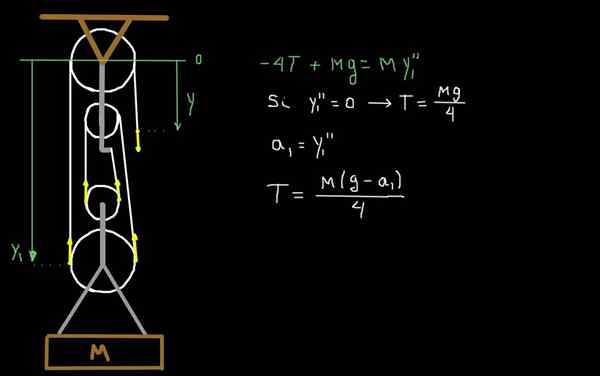Rajah 4. Dinamik pelantar faktorial.

Dalam Rajah 4 kita menarik daya kerana ketegangan T tali. Bahagian mudah alih rig mempunyai jumlah jisim m. Kita ambil sebagai sistem rujukan satu pada tahap pulley tetap dan positif yang pertama.

Y1 adalah kedudukan paksi pulley terendah.

Kami memohon undang -undang kedua Newton untuk menentukan pecutan A1 bahagian mudah alih rig:

Boleh melayani anda: teorem varignon

-4 t + mg = m a1

Oleh kerana berat beban adalah p = mg, di mana g adalah pecutan graviti, hubungan sebelumnya boleh ditulis:

-4T + P = P (A1 / G)

Jika kita ingin menentukan ketegangan yang digunakan dalam tali apabila beban berat tertentu dipercepatkan dengan pecutan A1, maka hubungan sebelumnya akan seperti ini:

T = p (1 - a1 / g) / 4

Perhatikan bahawa jika sistem sedang berehat atau bergerak secara berterusan, maka a1 = 0, dan kami pulih ungkapan yang sama yang kami perolehi dalam kes 2.

Latihan 3

Dalam contoh ini rig yang sama Latihan 1 digunakan, dengan tali yang sama yang menyokong maksimum 60 kg ketegangan. Beban tertentu meningkat, mempercepatkannya dari rehat hingga 1 m/s oleh 0.5 s, menggunakan ketegangan maksimum tali. Cari berat beban maksimum.

Penyelesaian

Kami akan menggunakan ungkapan yang diperolehi dalam Latihan 2 dan sistem rujukan dalam Rajah 4 di mana alamat positif adalah menegak ke bawah.

Percepatan beban ialah a1 = (-1 m/s -0 m/s) /0.5 s = -2 m/s^2.

Berat beban dalam kuasa kilogram diberikan oleh

P = 4 t / (1 - a1 / g)

P = 4*60 kg / (1 + 2/9.8) = 199.3 kg

Ini adalah berat maksimum beban beban tanpa tali yang rosak. Perhatikan bahawa nilai yang diperolehi kurang daripada yang diperolehi dalam Contoh 1, di mana beban itu sepatutnya dengan pecutan sifar, iaitu, pada waktu rehat atau kelajuan tetap.

Rujukan

1. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. 101-120.
2. Resnick, r. (1999). Fizikal. Vol. 1. 3 ra ed. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V. 87-103.
3. Giancoli, d. 2006. Fizik: Prinsip dengan aplikasi. 6th. Ed. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Sains Fizikal Konsep. 5th. Ed. Pearson.38-61.
5. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage. 100 - 119.