Arc (Geometry) Ukur, Jenis Gerbang, Contoh

Dia tunduk, Dalam geometri, ia adalah sebarang garis melengkung yang menghubungkan dua mata. Garis melengkung, tidak seperti garis lurus, adalah arah yang berbeza pada setiap titik yang sama. Kebalikan dari arka adalah segmen, kerana ini adalah bahagian lurus yang bergabung dengan dua mata.

Arka yang paling kerap digunakan dalam geometri adalah arka lilitan. Gerbang lain penggunaan biasa adalah gerbang parabola, lengkungan elips dan lengkungan catenary. Bentuk arka juga sering digunakan dalam seni bina sebagai elemen hiasan dan elemen struktur. Inilah kes lintel pintu dan tingkap, serta jambatan dan saluran air.

Rajah 1. Pelangi adalah garis melengkung yang bergabung dengan dua mata di kaki langit. Sumber: Pixabay

[TOC]

Arka dan ukurannya

Ukuran arka adalah panjangnya, yang bergantung pada jenis lengkung yang menghubungkan dua titik dan lokasi mereka.

Panjang arka bulat adalah salah satu yang paling mudah untuk dikira, kerana panjang arka penuh atau perimeter bulatan diketahui.

Perimeter bulatan adalah dua pi kali radio anda: P = 2 π r. Mengetahui ini, jika anda ingin mengira panjangnya s gerbang sudut bulat α (diukur dalam radian) dan radio R, Perkadaran digunakan:

(s / p) = (α / 2 π)

Kemudian membersihkan s dari ungkapan sebelumnya dan menggantikan perimeter p oleh ungkapannya bergantung pada radio R, Kamu ada:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α r.

Iaitu ukuran arka bulat adalah hasil pembukaan sudutnya oleh jejari arka bulat.

Untuk arka dengan cara umum masalahnya lebih rumit, sehingga para pemikir besar zaman dahulu mendakwa bahawa itu adalah tugas yang mustahil.

Ia dapat melayani anda: apakah ungkapan algebra dan yang paling kerap?

Tidak sampai kedatangan kalkulus pembezaan dan integral pada tahun 1665, bahawa masalah ukuran arka diselesaikan dengan memuaskan. 

Sebelum ciptaan kalkulus pembezaan, hanya penyelesaian yang dapat dijumpai melalui penggunaan garis poligonal atau lengkungan lilitan yang mendekati gerbang sebenar, tetapi penyelesaian ini tidak tepat. 

Jenis gerbang

Dari sudut pandangan geometri, gerbang diklasifikasikan mengikut garis melengkung yang bergabung dengan dua titik pesawat. Terdapat klasifikasi lain mengikut penggunaan dan bentuk seni bina.

Arka bulat

Apabila garis yang menghubungkan dua titik satah adalah sekeping lilitan jejari tertentu, terdapat arka bulat. Rajah 2 menunjukkan arka bulat radius r yang menghubungkan titik a dan b.

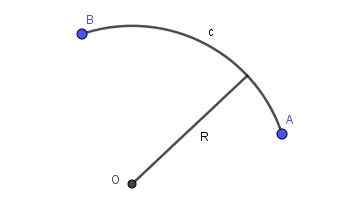Rajah 2. Arka bulat radio r yang menghubungkan titik a dan b. Disediakan oleh Ricardo Pérez.

Arka parabola

Perumpamaan adalah trajektori yang mengikuti objek yang telah dibuang ke udara dalam bentuk serong. Apabila lengkung yang menyertai dua mata adalah perumpamaan, maka ada gerbang parabola seperti yang ditunjukkan dalam Rajah 3.

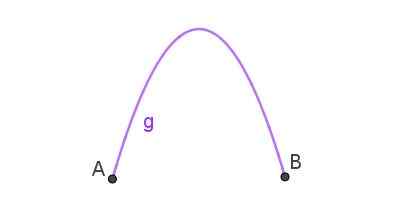Rajah 3. Arka parabola yang menghubungkan titik a dan b. Disediakan oleh Ricardo Pérez.

Inilah bentuk yang mengamalkan jet air yang keluar dari hos yang menunjukkan. Gerbang parabola dapat diperhatikan di sumber air.

Rajah 4. Arka parabola dibentuk oleh air dari sumber di Dresden. Sumber: Pixabay.

Catenary Arc

Arka catenary adalah lengkungan semulajadi yang lain. Catenary adalah lengkung yang secara semula jadi terbentuk apabila rantai atau tali tergantung dengan selesa dari dua titik berasingan.

Dapat melayani anda: apakah unsur -unsur sudut?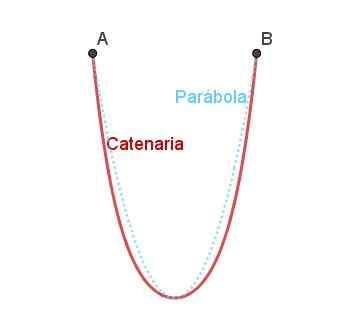 Rajah 5. Arka catenary dan perbandingan dengan gerbang parabola. Disediakan oleh Ricardo Pérez.

Catenary sama dengan parabola, tetapi ia tidak sama seperti yang dapat diperhatikan dalam Rajah 4.

Gerbang berbentuk catenary terbalik digunakan dalam seni bina sebagai elemen struktur rintangan mampatan yang tinggi. Malah, ia dapat ditunjukkan bahawa ia adalah jenis arka yang paling tahan di antara semua bentuk yang mungkin. 

Untuk membina arka catenary pepejal, hanya bentuk tali atau rantai disalin, maka bentuk yang disalin bertukar untuk menghasilkannya di pintu lintel atau tingkap.

Arka elips

Arka adalah elips jika lengkung yang menghubungkan dua mata adalah regangan atau elips. Ellipse ditakrifkan sebagai tempat geometri mata yang jaraknya ke dua mata yang diberikan selalu menambah jumlah yang tetap.

Ellipse adalah lengkung yang muncul dalam alam: ia adalah lengkung trajektori planet di sekitar matahari, seperti yang ditunjukkan oleh Johannes Kepler pada tahun 1609.

Dalam amalan, elips boleh ditarik dengan menetapkan dua tali di lantai atau dua pin di atas kertas dan mengikat tali kepada mereka. Maka tali itu tegang dengan penanda atau pensil dan lengkungnya ditarik. Sekeping elips adalah lengkungan elips. Animasi berikut menggambarkan bagaimana elips ditarik:

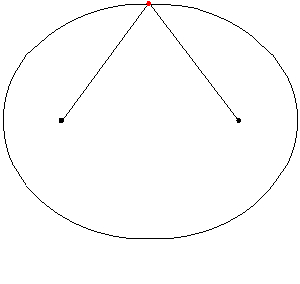Rajah 5. Posen elips menggunakan tali tegang. Sumber: Wikimedia Commons

Rajah 6 menunjukkan arka elips yang menghubungkan titik g dan h.

Rajah 6. Arka elips yang menghubungkan dua mata. Disediakan oleh Ricardo Pérez.

Contoh gerbang

Contoh berikut merujuk kepada cara mengira perimeter beberapa gerbang tertentu.

Boleh melayani anda: nombor transenden: apakah, formula, contoh, latihan

Contoh 1

Rajah 7 menunjukkan tingkap yang berakhir dengan arka pekeliling potong. Dimensi yang ditunjukkan dalam angka itu berada di kaki. Kirakan panjang arka.

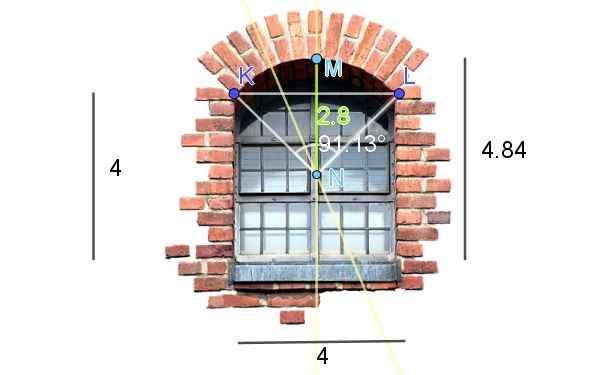Rajah 7. Pengiraan panjang arka bulat tetingkap. (Anotasi Sendiri - Imej Tetingkap di Pixabay)

Untuk mendapatkan pusat dan jejari arka bulat lintel tetingkap, pembinaan berikut dibuat pada imej:

-Segmen KL ditarik dan meditrixnya ditarik.

-Kemudian titik tertinggi lintel terletak, yang kami panggil m. Segmen KM kemudian dipertimbangkan dan meditrixnya ditarik.

Pemintasan kedua -dua mediumtrices adalah titik n dan juga pusat arka bulat.

-Sekarang anda perlu mengukur panjang segmen NM, yang bertepatan dengan radius r arka bulat: r = 2.8 kaki.

-Untuk mengetahui panjang arka sebagai tambahan kepada jejari, sudut yang membentuk arka. Yang boleh ditentukan oleh dua kaedah, atau diukur dengan pengangkut, atau dikira secara bergantian menggunakan trigonometri.

Dalam kes yang menunjukkan sudut yang membentuk arka adalah 91,13º, yang mesti ditukar kepada radian:

 91,13º = 91,13º * π / 180º = 1.59 radian

Kami akhirnya mengira panjang s arka melalui formula S = α r.

S = 1.59 * 2.8 kaki = 4.45 kaki

Contoh 2

Cari panjang arka elips yang ditunjukkan dalam Rajah 8, yang diketahui r dan semi -axis kecil s daripada Ellipse.

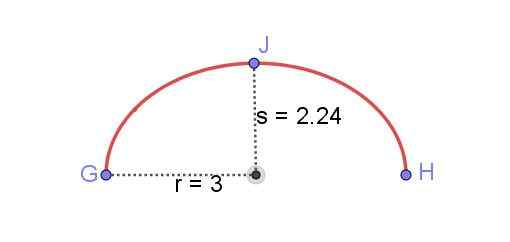Rajah 8. Arka elips antara gh. Disediakan oleh Ricardo Pérez.

Mencari panjang elips adalah untuk masa yang lama salah satu masalah matematik yang paling sukar. Penyelesaian yang dinyatakan oleh integral elips boleh diperoleh tetapi mempunyai nilai berangka, integral dalam siri kuasa mesti diperluas. Hasil yang tepat akan memerlukan syarat -syarat yang tidak terhingga dari siri tersebut.

Nasib baik, genius matematik asal Hindu Ramanujan, yang tinggal di antara tahun 1887 dan 1920, mendapati formula yang menghampiri perimeter elips:

Perimeter elips = π [3 (r + s) - √ ((3r + s) (r + 3s))]]

Perimeter elips dengan r = 3 cm dan s = 2.24 cm ialah 16.55 cm. Walau bagaimanapun, gerbang elips yang ditunjukkan mempunyai separuh daripada nilai itu:

Panjang arka elips GH = 8.28 cm.

Rujukan

1. Clemens s. 2008. Geometri dan trigonometri. Pendidikan Pearson.
2. Garcia f. Prosedur berangka di Java. Panjang elips. Diperolehi dari: sc.Ehu.adalah
3. Geometri dinamik. Gerbang. Pulih dari geometriadinamica.adalah
4. Pize. Elips dan perumpamaan di sekeliling kita. Diperolehi dari: Pizeas.com
5. Wikipedia. Arka (geometri). Pulih dari: ia adalah.Wikipedia.com