Pusat sifat graviti, pengiraan, contoh

Dia Pusat Graviti badan saiz yang boleh diukur adalah titik di mana beratnya dianggap digunakan. Oleh itu, ia adalah salah satu konsep utama statik.

Pendekatan pertama dalam masalah fizik asas adalah untuk mengandaikan bahawa mana -mana objek bertindak sebagai jisim tertentu, iaitu, ia tidak mempunyai dimensi dan keseluruhan jisim tertumpu dalam satu titik. Ini sah untuk kotak, kereta, planet atau zarah subatomik. Model ini dikenali sebagai Model zarah.

Rajah 1. Di ketinggian melompat atlet membetulkannya sehingga pusat gravitinya berada di luar badan. Sumber: Pixabay

Sememangnya ini adalah pendekatan, yang memberikan hasil yang sangat baik untuk banyak aplikasi. Bukan tugas yang mudah untuk mempertimbangkan tingkah laku individu ribuan dan berjuta -juta zarah yang boleh dimiliki oleh objek.

Walau bagaimanapun, dimensi sebenar perkara perlu diambil kira jika anda mahu. Oleh kerana kita biasanya berada di sekitar bumi, kekuatan yang sentiasa ada di mana -mana badan adalah tepat berat.

[TOC]

Pertimbangan untuk mencari pusat graviti 

Sekiranya saiz badan akan diambil kira, di mana beratnya akan digunakan secara khusus? Apabila anda mempunyai objek berterusan sewenang -wenangnya, beratnya adalah Daya yang diedarkan antara setiap zarah konstituennya.

Biarkan zarah -zarah ini m₁, m₂, m₃... masing -masing mengalami daya graviti yang sama m₁g, m₂g, m₃G ..., semua selari. Ini begitu, kerana medan graviti bumi dianggap tetap dalam kebanyakan kes, memandangkan objek itu kecil berbanding saiz planet dan dekat dengan permukaannya.

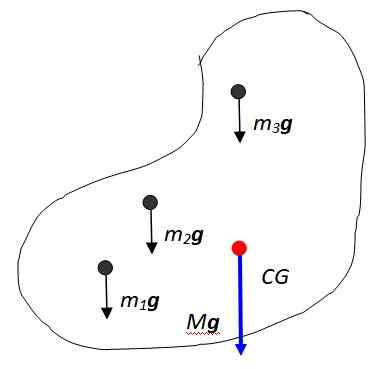Rajah 2. Berat objek adalah jisim yang diedarkan. Sumber: Diri Diri.

Jumlah vektor daya ini mengakibatkan berat objek, yang digunakan pada titik yang disebut pusat graviti yang dilambangkan dalam angka sebagai CG, yang kemudiannya bertepatan dengan Pusat Massa. Pusat massa pada gilirannya adalah titik di mana seluruh jisim boleh dianggap tertumpu.

Berat yang dihasilkan mempunyai magnitud Mg di mana M Ia adalah jumlah jisim objek, dan tentu saja ia diarahkan secara menegak ke arah pusat bumi. Notasi Sumory berguna untuk menyatakan jumlah badan badan:

Objek simetri dan homogen, yang bersamaan dengan ketumpatan mereka yang seragam, mempunyai pusat graviti mereka di pusat geometri: kiub, paralelepiped, cincin, tayar atau sfera.

Pusat graviti tidak selalu sesuai dengan titik material. Sebagai contoh, CG gelung berada di pusat geometri, di mana tidak ada doh sendiri. Walaupun begitu, jika anda ingin menganalisis kekuatan yang bertindak pada gelung, beratnya mesti digunakan untuk titik yang tepat ini.

Di mana kes -kes di mana objek itu sewenang -wenangnya, jika ia homogen, pusat jisimnya masih boleh dikira dengan mencari Centroid o Baricentro dari angka itu.

Boleh melayani anda: Mercury (planet)

Bagaimana pusat graviti dikira?

Pada dasarnya jika pusat graviti (CG) dan pusat jisim (cm) bertepatan apabila medan graviti seragam, maka CM dapat dikira dan di atasnya menggunakan berat badan.

Pertimbangkan dua kes: Yang pertama adalah satu di mana pengedaran massa adalah bijak; iaitu, anda boleh mengira setiap jisim yang membentuk sistem dan memberikan nombor I, seperti yang dilakukan dalam contoh sebelumnya.

Koordinat pusat jisim untuk pengedaran massa diskret adalah: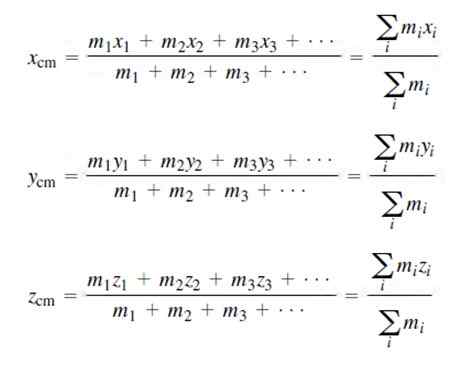

Secara semulajadi jumlah semua massa bersamaan dengan jumlah jisim sistem m, seperti yang ditunjukkan di atas.

Tiga persamaan dikurangkan kepada bentuk padat apabila mempertimbangkan vektor r r_cm o Posisi Vektor Pusat Massa:

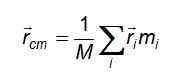
Dan dalam hal pengagihan massa yang berterusan, di mana zarah -zarah adalah saiz pembezaan dan tidak dapat dibezakan untuk mengira mereka, jumlahnya digantikan dengan integral yang dibuat tentang jumlah yang diduduki oleh objek yang dipersoalkan:

Di mana r Ia adalah vektor kedudukan jisim pembezaan DM Dan definisi ketumpatan massa untuk menyatakan perbezaan massa telah dibuat DM terkandung dalam perbezaan isipadu Dv:

Ketumpatan objek boleh tetap, di mana ia keluar dari integral, atau menjadi fungsi koordinat spatial dan kita mesti tahu pergantungannya pada (x, y, z) untuk menyelesaikan integral.

Sifat

Beberapa pertimbangan penting mengenai pusat massa adalah seperti berikut:

- Walaupun sistem rujukan diperlukan untuk menubuhkan kedudukan, pusat jisim tidak bergantung pada pilihan yang dibuat dari sistem, karena itu adalah milik objek tersebut.

- Apabila objek mempunyai paksi atau satah simetri, pusat massa berada di paksi atau satah tersebut. Manfaatkan keadaan ini menjimatkan masa pengiraan.

- Semua daya luaran yang bertindak pada objek boleh digunakan di pusat massa. Mengikuti jejak perkara ini memberikan idea global mengenai pergerakan objek dan memudahkan kerja mengkaji kelakuannya.

-Mencari pusat graviti badan dalam keseimbangan statik

Katakan bahawa badan angka sebelumnya berada dalam baki statik adalah.

Rajah 3. Skim untuk mengira tork berat berkenaan dengan titik atau.

Momen kilasan bersih berkenaan dengan O, menurut Rajah 3 adalah: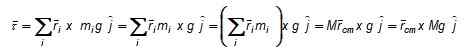A. Besarnya F dipilih supaya objek tidak dipindahkan sama ada dan dengan cara ini kita akan memilikinya dalam keseimbangan statik.

Boleh melayani anda: optik bergelora

-Contoh yang diselesaikan

Bar nipis bahan seragam mempunyai panjang 6 m dan berat 30 n. Pada akhirnya, 50 n barat dan satu lagi 20 n di hujung kanannya digantung. Cari: a) Besarnya daya menaik yang diperlukan untuk mengekalkan keseimbangan bar, b) pusat graviti set.

Penyelesaian

Gambar rajah daya ditunjukkan dalam angka berikut. Berat bar digunakan di pusat graviti, yang bertepatan dengan pusat geometri. Satu -satunya dimensi bar yang diambil kira adalah panjangnya, kerana pernyataan itu memberitahu bahawa ia adalah nipis.

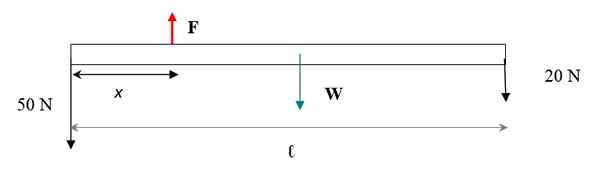Rajah 4. Pàra La Barra Diagram.

Untuk sistem berat bar + untuk kekal dalam keseimbangan terjemahan, jumlah daya mesti dibatalkan. Kekuatan menegak, jika kita mempertimbangkan dengan tanda + dan ke bawah dengan tanda - maka:

F- 50- 20-30 N = 0

F = 100 n

Kekuatan ini menjamin keseimbangan terjemahan. Mengambil momen kilasan semua kuasa mengenai paksi yang melewati hujung kiri sistem dan memohon definisi:

t = r x f

Momen semua kuasa ini berkenaan dengan titik yang dipilih berserenjang dengan satah bar:

t_F = xf = 100x

t_W = -(l/2) mg = -3m . 30 n = -90 n.m

t₁ = 0 (Oleh kerana kekuatan 50 n melewati paksi putaran yang dipilih dan tidak bersenam)

t₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Oleh itu:

100 x -90 -120 N.m = 0

x = 2.10 m

Pusat graviti bar bar + berat terletak pada 2.10 meter dari hujung kiri bar.

Perbezaan dengan pusat jisim

Pusat graviti bertepatan dengan pusat jisim, seperti yang ditunjukkan, selagi medan graviti tanah tetap untuk semua titik objek yang harus dipertimbangkan. Bidang graviti bumi tidak lain selain nilai yang terkenal dan biasa g = 9.8 m/s² diarahkan secara menegak.

Walaupun nilai g mengalami variasi dengan latitud dan ketinggian, mereka biasanya tidak mempengaruhi objek yang mana kebanyakan masa dirawat. Sangat berbeza jika dianggap sebagai badan besar di sekitar bumi, contohnya asteroid yang akan dekat dengan planet ini.

Asteroid mempunyai pusat jisimnya sendiri, tetapi pusat graviti tidak lagi perlu bertepatan dengan ini, sejak itu g Ia mungkin akan mengalami variasi yang besar dalam magnitud, memandangkan saiz asteroid dan berat setiap zarah mungkin tidak selari.

Perbezaan asas lain ialah pusat jisim tidak kira sama ada atau tidak ada daya yang dipanggil berat yang digunakan pada objek tersebut. Ia adalah harta intrinsik objek yang mendedahkan bagaimana jisimnya diedarkan berhubung dengan geometrinya.

Boleh melayani anda: apakah pemalar dielektrik?

Pusat Massa wujud jika ada berat yang digunakan seolah -olah tidak. Dan terletak di kedudukan yang sama walaupun objek dipindahkan ke planet lain di mana medan graviti berbeza.

Sebaliknya, pusat graviti jelas dikaitkan dengan penggunaan berat badan, kerana kami dapat menghargai sepanjang perenggan sebelumnya.

Contoh Pusat Graviti

Pusat graviti objek yang tidak teratur

Sangat mudah untuk mengetahui di mana pusat graviti objek yang tidak teratur adalah seperti cawan. Pertama ia digantung dari mana -mana titik dan dari sana garis menegak ditarik (dalam Rajah 5 ia adalah garis fuchsia di imej kiri).

Kemudian ia digantung dari titik lain dan garis menegak baru (garis biru dalam imej yang betul) ditarik. Persimpangan kedua -dua baris adalah pusat graviti cawan.

Rajah 5 . CG Lokasi cawan. Sumber: Pixabay yang diubahsuai.

Keseimbangan objek

Mari kita menganalisis kestabilan trak yang beredar di sepanjang jalan. Apabila pusat graviti berada di atas pangkal trak, ia tidak akan mencurahkan. Imej di sebelah kiri adalah kedudukan yang paling stabil.

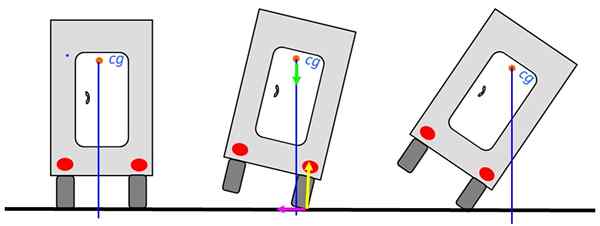Rajah 6. Baki trak. Sumber: Diri Diri.

Walaupun trak bersandar di sebelah kanan boleh kembali ke kedudukan keseimbangan yang stabil, seperti dalam lukisan medium, kerana menegak masih melalui pangkalan. Walau bagaimanapun, apabila garis ini berlalu di luar trak akan bertukar.

Gambar rajah menunjukkan daya di titik sokongan: normal dalam kuning, berat hijau dan geseran statik ke kiri di fuchsia. Normal dan menggosok. Oleh itu mereka tidak akan menyumbang untuk membuang trak.

Berat tetap, yang menjalankan momen kilasan, bernasib baik dalam pengertian anti -horary dan yang cenderung kembali ke trak ke kedudukan keseimbangannya. Perhatikan bahawa garis menegak melalui permukaan sokongan, iaitu tayar.

Apabila trak berada di kedudukan yang melampau, masa kilasan berat badan dan menjadi arah yang tegang. Tidak dapat ditangguhkan pada masa yang lain, trak akan mencurahkan.

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.  247-253.
2. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6 ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fizikal. Vol. 1. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V. 331-341.
4. Rex, a. 2011. Asas Fizik. Pearson.146-155.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.340-346.