Klasifikasi nombor sebenar

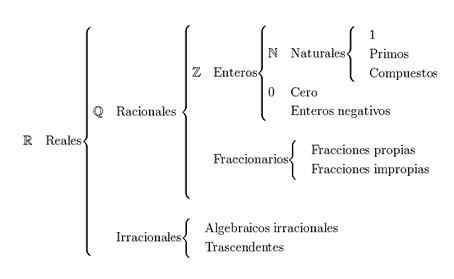
Yang utama Klasifikasi nombor sebenar Ia dibahagikan kepada nombor semula jadi, nombor keseluruhan, nombor rasional dan nombor yang tidak rasional. Nombor sebenar diwakili dengan huruf r.

Nombor sebenar merujuk kepada gabungan kumpulan nombor rasional dan tidak rasional. Untuk membentuk kumpulan ini, nombor semula jadi dan nombor keseluruhan diperlukan.

Terdapat banyak cara di mana bilangan sebenar yang berbeza boleh dibina atau diterangkan, berbeza dari bentuk yang lebih mudah ke bentuk yang lebih kompleks, bergantung kepada kerja matematik yang ingin anda lakukan.

Bagaimana nombor sebenar dikelaskan?

- Nombor semula jadi

Nombor semula jadi diwakili oleh huruf (n) dan yang digunakan untuk mengira (0.1,2,3,4 ...). Contohnya "ada lima belas Rosas di Taman "," Penduduk Mexico berasal dari 126 berjuta -juta orang "atau" jumlah dua dan dua adalah empat". Harus diperhatikan bahawa beberapa klasifikasi termasuk 0 sebagai nombor semula jadi dan yang lain tidak. 

Dua kanak -kanak membuat jumlah dua nombor semula jadi.

Nombor semula jadi tidak termasuk mereka yang mempunyai bahagian perpuluhan. Oleh itu, "Penduduk Mexico berasal dari 126.2 berjuta -juta orang "atau" membuat suhu 24.5 Celsius Derajat ”Nombor semula jadi tidak dapat dipertimbangkan.

Dalam bahasa yang sama, seperti sekolah rendah, nombor semulajadi boleh dipanggil nombor perakaunan untuk mengecualikan bilangan bulat negatif dan sifar.

Nombor semulajadi adalah pangkalan yang mana banyak nombor lain boleh dibina dengan lanjutan: nombor keseluruhan, nombor rasional, nombor nyata dan nombor kompleks, antara lain.

Ciri -ciri nombor semula jadi, seperti pembahagian dan pengedaran nombor utama, dikaji dalam teori nombor. Masalah yang berkaitan dengan pengiraan dan pesanan, seperti penghitungan dan partition, dikaji dalam kombinatorial.

Mereka mempunyai beberapa sifat, seperti: jumlah, pendaraban, penolakan, pembahagian, dll.

Boleh melayani anda: sains kontemporari

Nombor ordinal dan kardinal

Nombor semula jadi boleh menjadi ordinal atau kardinal.

Nombor kardinal akan digunakan sebagai nombor semula jadi, seperti yang disebutkan di atas dalam contoh. "Ada dua Kuki "," Saya adalah bapa tiga kanak -kanak "," Kotak itu termasuk dua Krim Hadiah ". 

Ordinan adalah yang menyatakan perintah atau menunjukkan kedudukan. Sebagai contoh, dalam perlumbaan, perintah ketibaan pelari disenaraikan oleh pemenang dan menamatkan yang terakhir yang datang ke garisan penamat.

Dengan cara ini, akan dikatakan bahawa pemenang adalah "pertama", yang seterusnya "kedua", yang seterusnya "ketiga" dan sebagainya sehingga yang terakhir. Nombor -nombor ini boleh diwakili oleh huruf di sebelah kanan atas untuk memudahkan penulisan (1, ke -2, ke -3, ke -4, dll.).

- Nombor integer

Keseluruhan nombor terdiri daripada nombor semulajadi dan bertentangan mereka, iaitu, nombor negatif (0, 1, -1, 2, -2, 50, -50 ...). Seperti nombor semula jadi, ini tidak termasuk mereka yang mempunyai bahagian perpuluhan.

Contoh seluruh nombor akan menjadi "purata ke -30 di Jerman", "saya tinggal di 0 setelah sampai ke akhir bulan", "untuk turun ke ruang bawah tanah, anda mesti menandakan butang lif" lif ".

Sebaliknya, nombor keseluruhan tidak dapat ditulis dengan komponen pecahan. Contohnya, nombor seperti 8.58 atau √2 bukan nombor keseluruhan.

Nombor keseluruhan diwakili dengan huruf (z). Z adalah kumpulan submail nombor rasional q, yang seterusnya membentuk kumpulan nombor sebenar n. Seperti nombor semula jadi, Z adalah kumpulan perakaunan yang tidak terhingga.

Bilangan bulat membentuk kumpulan terkecil dan set nombor semula jadi terkecil. Dalam teori nombor algebra, nombor keseluruhan kadang -kadang dipanggil tidak rasional untuk membezakannya dari bilangan bulat algebra.

Ia boleh melayani anda: projek penyelidikan: pihak, bagaimana ia dijelaskan dan contohnya

- Nombor rasional

Set nombor rasional diwakili oleh huruf (q) dan memasukkan semua nombor yang boleh ditulis sebagai sebahagian kecil daripada nombor keseluruhan.

Iaitu, set ini termasuk nombor semula jadi (4/1), nombor keseluruhan (-4/1) dan nombor perpuluhan yang tepat (15,50 = 1550/100).

Pengagihan 1/6 keju adalah nombor rasional.

Pengembangan perpuluhan nombor rasional selalu berakhir selepas bilangan digit yang terhingga (misalnya 15.50) atau ketika urutan angka yang sama dari digit mulai diulangi lagi dan lagi (misalnya 0.34566666666666 ...). Oleh itu, dalam set nombor rasional nombor dimasukkan. surat khabar tulen atau surat khabar bercampur.

Di samping itu, sebarang perpuluhan berulang atau terminal mewakili nombor rasional. Kenyataan ini benar bukan sahaja untuk asas 10, tetapi juga untuk nombor asas lain.

Bilangan sebenar yang tidak rasional dipanggil tidak rasional. Nombor tidak rasional termasuk √2, π dan e, contohnya. Oleh kerana keseluruhan set nombor rasional adalah kebas, dan kumpulan nombor sebenar tidak boleh dibasuh, dapat dikatakan bahawa hampir semua nombor nyata tidak masuk akal.

Nombor rasional boleh ditakrifkan secara rasmi sebagai kelas kesetaraan pasangan keseluruhan (p, q) supaya q ≠ 0 atau hubungan setara yang ditakrifkan oleh (p1, q1) (p2, q2) hanya jika p1, q2 = p2q1.

Nombor rasional, bersama -sama dengan jumlah dan pendaraban, bidang bentuk yang membentuk seluruh nombor dan terkandung oleh mana -mana cawangan yang mengandungi keseluruhan.

- Nombor tidak rasional

Nombor tidak rasional adalah semua nombor sebenar yang bukan nombor rasional; Nombor tidak rasional tidak dapat dinyatakan sebagai pecahan. Nombor rasional adalah nombor yang terdiri daripada pecahan nombor keseluruhan.

Akibat ujian penyanyi yang mengatakan bahawa semua nombor nyata tidak dapat dihubungkan dan bahawa rasional jika mereka adalah nombor, dapat disimpulkan bahawa hampir semua nombor nyata adalah tidak rasional.

Boleh melayani anda: trajektori dan anjakan

Apabila radius dua segmen baris adalah nombor yang tidak rasional, dapat dikatakan bahawa segmen garis ini tidak dapat diukur; bermaksud bahawa tidak ada panjang yang mencukupi sehingga masing -masing dapat "mengukur" dengan integer tertentu yang sama.

Di antara nombor yang tidak rasional ialah jejari π dari bulatan bulatan ke diameternya, bilangan euler (e), nombor emas (φ) dan akar kuadrat dua; Lebih -lebih lagi, semua akar persegi nombor semula jadi tidak masuk akal. Satu -satunya pengecualian untuk peraturan ini adalah dataran yang sempurna.

Dapat diperhatikan bahawa apabila nombor tidak rasional dinyatakan secara kedudukan dalam sistem angka, (seperti nombor perpuluhan) tidak berakhir atau ulangi.

Ini bermakna bahawa mereka tidak mengandungi urutan digit, pengulangan yang mana garis perwakilan dibuat.

Penyederhanaan nombor tidak rasional pi.

Contohnya: Perwakilan perpuluhan nombor π bermula dengan 3.14159265358979, tetapi tidak ada bilangan digit yang dapat mewakili π tepat, dan tidak dapat diulangi.

Bukti bahawa pengembangan perpuluhan nombor rasional mesti berakhir atau diulang adalah berbeza dari bukti bahawa lanjutan perpuluhan mestilah nombor rasional; Walaupun asas dan agak panjang, ujian ini mengambil kerja.

Biasanya ahli matematik tidak biasanya mengambil tanggapan "mengakhiri atau mengulangi" untuk menentukan konsep nombor rasional.

Nombor tidak rasional juga boleh dirawat melalui pecahan yang tidak berterusan.

Rujukan

1. Klasifikasi nombor sebenar. Pulih dari Chilimath.com.
2. Nombor semula jadi. Pulih dari Wikipedia.org.
3. Klasifikasi nombor. Ditutor pulih.com.
4. Pulih dari Wikipedia.org.
5. Nombor tidak rasional. Pulih dari Wikipedia.org.