Konsep pekali konsep, formula, pengiraan, contoh

Dia pekali pemulihan Ini adalah kota antara kelajuan laju relatif dan kelajuan relatif menghampiri dua badan yang bertembung. Apabila mayat bersatu selepas perlanggaran, kuil ini tidak sah. Dan unit itu bernilai sekiranya perlanggaran itu sangat elastik.

Katakan dua sfera jisim pepejal M1 dan jisim M2 masing -masing bahawa mereka mengalami perlanggaran. Sebelum perlanggaran sfera mempunyai kelajuan V1 dan V2 Mengenai sistem rujukan inersia tertentu. Sebaik sahaja perlanggaran kelajuan mereka berubah menjadi V1 ' dan V2 '.

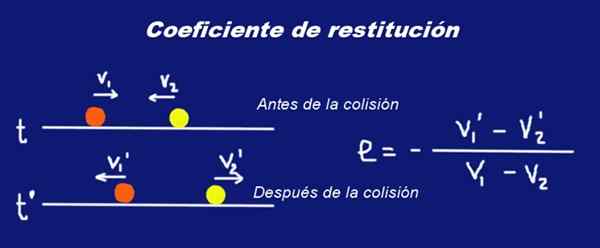Rajah 1. Perlanggaran dua sfera massa M1 dan M2 dan pekali pengembalian mereka dan. Disediakan oleh Ricardo Pérez.

Surat telah diletakkan Font Bold Dalam kelajuan untuk menunjukkan bahawa mereka adalah kuantiti vektor.

Eksperimen menunjukkan bahawa setiap perlanggaran memenuhi hubungan berikut:

V1 ' - V2 '= -dan (V1 - V2)

Di mana dan Ia adalah nombor sebenar antara 0 dan 1, yang dipanggil pekali pemulihan dari perlanggaran. Ungkapan sebelumnya ditafsirkan seperti berikut: 

Kelajuan relatif dua zarah sebelum perlanggaran adalah berkadar dengan kelajuan relatif kedua-dua zarah selepas perlanggaran, pemalar perkadaran adalah (-e), di mana e adalah pekali pemulihan perlanggaran.

[TOC]

Apakah pekali restitusi untuk?

Kegunaan pekali ini terletak pada mengetahui Ijazah Ketidakstabilan perlanggaran. Sekiranya perlanggaran adalah elastik yang sempurna, pekali akan menjadi 1, manakala dalam perlanggaran yang tidak jelas, pekali akan bernilai 0, kerana dalam kes ini, kelajuan relatif selepas perlanggaran adalah batal.

Secara kebetulan, jika pekali pengembalian perlanggaran dan kelajuan zarah diketahui sebelum ini, maka kelajuan dapat diramalkan setelah berlanggar tersebut terjadi. 

Boleh melayani anda: 13 contoh undang -undang pertama Newton dalam kehidupan sebenar

Momentum

Dalam perlanggaran, sebagai tambahan kepada hubungan yang ditubuhkan oleh pekali restitusi, terdapat satu lagi hubungan asas, iaitu Pemuliharaan Momentum.

Momentum p zarah, atau jumlah pergerakan seperti yang dipanggil juga, ia adalah produk jisim M zarah untuk kelajuannya V. Iaitu: momentum p Ia adalah jumlah vektor.

Dalam perlanggaran momentum linear P Sistem ini adalah sama sebelum dan hanya selepas perlanggaran, kerana daya luaran hina terhadap daya singkat tetapi sengit interaksi dalaman semasa perlanggaran. Tetapi pemuliharaan momentum tidak mencukupi P sistem untuk menyelesaikan masalah umum perlanggaran.

Dalam kes yang disebutkan sebelumnya, kedua -dua sfera M1 dan M2 yang bertembung, pemuliharaan momentum linear ditulis seperti ini:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Tidak ada cara untuk menyelesaikan masalah perlanggaran jika pekali pengembalian tidak diketahui. Pemuliharaan momentum, walaupun perlu, tidak mencukupi untuk meramalkan kelajuan selepas perlanggaran.

Apabila masalah menyatakan bahawa mayat bergerak bersama selepas perlanggaran, secara tersirat mengatakan bahawa pekali pengembalian adalah 0.

Rajah 2. Dalam bola biliard terdapat perlanggaran pekali restitusi sedikit kurang dari 1. Sumber: Pixabay.

Koefisien tenaga dan pengembalian 

Jumlah fizikal penting lain yang terlibat dalam perlanggaran adalah tenaga. Semasa perlanggaran terdapat pertukaran tenaga kinetik, tenaga berpotensi dan lain -lain jenis tenaga, seperti tenaga kalori.

Sebelum dan selepas perlanggaran tenaga berpotensi interaksi adalah hampir nih, jadi keseimbangan tenaga melibatkan tenaga kinetik zarah sebelum dan selepas dan jumlahnya Q dipanggil tenaga yang hilang.

Ia boleh melayani anda: Model Atom Heisenberg

Untuk kedua -dua sfera jisim M1 dan M2 yang bertembung keseimbangan tenaga sebelum dan selepas perlanggaran itu ditulis seperti ini:

½ m1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + q

Apabila daya interaksi semasa perlanggaran adalah semata -mata konservatif, ia berlaku Jumlah tenaga kinetik Zarah -zarah yang bertembung ia dipelihara, iaitu, ia adalah sama sebelum dan selepas perlanggaran (q = 0). Apabila ini berlaku, dikatakan bahawa perlanggaran sangat elastik.

Dalam kes perlanggaran elastik, tenaga tidak hilang. Dan juga pekali restitusi mematuhi: E = 1. 

Sebaliknya, dalam perlanggaran tidak elok yang ≠ 0 dan 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Untuk masalah perlanggaran yang ditentukan dengan sempurna, perlu mengetahui pekali pengembalian, atau bergantian jumlah tenaga yang hilang semasa perlanggaran.

Koefisien pengembalian bergantung pada sifat dan jenis interaksi antara kedua -dua badan semasa perlanggaran.

Sebaliknya, kelajuan relatif badan sebelum perlanggaran akan menentukan intensiti interaksi dan oleh itu pengaruhnya terhadap pekali restitusi. 

Bagaimana pekali restitusi dikira?

Untuk menggambarkan bagaimana pekali pemulihan perlanggaran dikira, kami akan mengambil kes yang mudah:

Katakan perlanggaran dua sfera massa M1 = 1 kg dan M2 = 2 kg yang bergerak pada geseran lurus (seperti dalam Rajah 1).

Sfera pertama mempengaruhi kelajuan awal V1 = 1 m/s Mengenai yang kedua yang pada asalnya berehat, itu V2 = 0 m/s.

Ia boleh melayani anda: Undang -undang Termodinamik Pertama: Formula, Persamaan, Contoh

Selepas perlanggaran mereka bergerak seperti ini: yang pertama berhenti (V1 '= 0 m/s) dan yang kedua bergerak ke kanan dengan kelajuan V2 '= 1/2 m/s.

Untuk mengira pekali restitusi dalam perlanggaran ini, kami menggunakan hubungan:

V1 ' - V2 ' = -dan ( V1 - V2 ) 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Contoh

Dalam perlanggaran satu -dimensi dari dua sfera bahagian sebelumnya, pekali restitusi dikira mengakibatkan E = ½ .

Sebagai e ≠ 1 perlanggaran tidak elastik, iaitu, tenaga kinetik sistem tidak dipelihara dan terdapat beberapa tenaga yang hilang q (contohnya pemanasan sfera kerana perlanggaran).

Tentukan nilai tenaga yang hilang dalam joules. Juga hitung pecahan peratusan tenaga yang hilang.

Penyelesaian

Tenaga kinetik awal sfera 1 adalah: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Sementara sfera 2 adalah sifar kerana pada mulanya berehat.

Jadi tenaga kinetik awal sistem adalah ki = ½ j.

Selepas perlanggaran hanya sfera kedua bergerak dengan kelajuan v2 '= ½ m/s, jadi tenaga kinetik akhir sistem akan menjadi:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j

Iaitu, tenaga yang hilang dalam perlanggaran adalah:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

Dan pecahan tenaga yang hilang dalam perlanggaran ini dikira seperti berikut:

F = q / ki = ¼ / ½ = 0.5 iaitu 50% tenaga sistem telah hilang kerana perlanggaran tidak elok yang pekali restitusi adalah 0.5.

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
3. Knight, r. 2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi. Pearson.
4. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.
5. Wikipedia. Jumlah pergerakan.Pulih dari: Adakah.Wikipedia.org.