Integrasi makna, pengiraan dan contoh yang berterusan

The Pemalar integrasi Ia adalah nilai tambah kepada pengiraan antiderivatif atau integral, ia berfungsi untuk mewakili penyelesaian yang membentuk primitif fungsi. Menyatakan kekaburan yang melekat di mana fungsi mana -mana mempunyai bilangan primitif yang tidak terhingga.

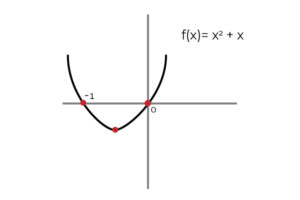
Contohnya jika fungsi diambil: f (x) = 2x + 1 dan kita mendapat antiderivatif:

∫ (2x+1) dx = x² + x + C ; Di mana C Ia adalah Pemalar integrasi dan secara grafik mewakili terjemahan menegak antara kemungkinan tak terhingga primitif. Betul untuk mengatakan bahawa (x² + x) Ia adalah a primitif f (x).

Sumber: Pengarang

Dengan cara yang sama anda boleh menentukan (x² + x + C ) sebagai primitif f (x).

[TOC]

Harta songsang

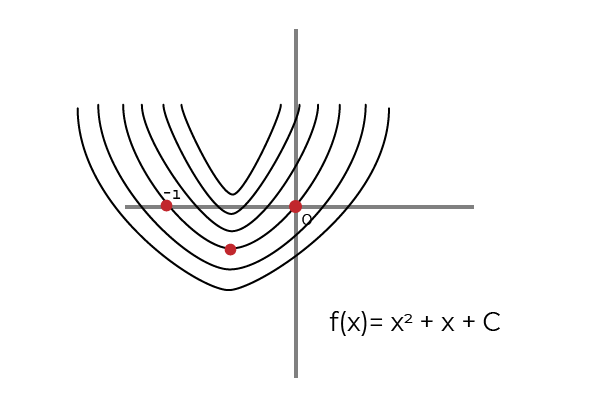
Dapat diperhatikan bahawa apabila berasaskan ungkapan (x² + x) Fungsi f (x) = 2x + 1 diperoleh. Ini disebabkan oleh harta songsang antara derivasi dan integrasi fungsi. Harta ini membolehkan untuk mendapatkan formula integrasi bermula dari pembezaan. Yang membolehkan pengesahan integral melalui derivatif yang sama.

Sumber: Pengarang

Walau bagaimanapun (x² + x) Bukan satu -satunya fungsi yang terbitannya sama dengan (2x + 1).

1. D (x² + x)/ dx = 2x + 1
2. D (x² + x + 1)/ dx = 2x + 1
3. D (x² + x + 2)/ dx = 2x + 1
4. D (x² + x + 3)/ dx = 2x + 1
5. D (x² + x + C)/ dx = 2x + 1

Di mana 1, 2, 3 dan 4 mewakili primitif tertentu f (x) = 2x + 1. Manakala 5 mewakili integral tak terbatas atau primitif f (x) = 2x + 1.

Sumber: Pengarang

Primitif fungsi dicapai melalui proses antiderivasi atau integral. Di mana f akan menjadi primitif f jika berikut dipenuhi

• y = ∫ f (x) dx = F (x) + c; C = Pemalar integrasi
• F '(x) = f (x)

Dihargai bahawa fungsi mempunyai derivatif tunggal, tidak seperti primitif tak terhingga yang terhasil daripada integrasi.

Integral yang tidak terbatas

 ∫ f (x) dx = f (x) + c

Ia sepadan dengan keluarga lengkung dengan corak yang sama, yang mengalami ketidakcocokan dalam nilai imej setiap titik (x, y). Setiap fungsi yang memenuhi corak ini akan menjadi primitif individu dan set semua fungsi dikenali sebagai Integral tidak terbatas.

Nilai Pemalar integrasi Ia akan menjadi yang membezakan setiap fungsi dalam amalan.

The Pemalar integrasi Ia mencadangkan anjakan menegak dalam semua graf yang mewakili primitif fungsi. Di mana paralelisme diperhatikan di antara mereka, dan hakikat bahawa C Ia adalah nilai anjakan.

Menurut amalan biasa Pemalar integrasi Ia dilambangkan dengan huruf "c" selepas penambahan, walaupun dalam praktiknya tidak acuh jika pemalar menambah atau menolak. Nilai sebenar boleh didapati dengan pelbagai cara mengikut berbeza keadaan awal.

Makna lain dari pemalar integrasi

Sudah ada perbincangan mengenai bagaimana Pemalar integrasi digunakan di cawangan kalkulus integral; Mewakili keluarga lengkung yang menentukan integral yang tidak terbatas. Tetapi banyak sains dan cawangan lain telah memberikan nilai yang sangat menarik dan praktikal Pemalar integrasi, yang telah memudahkan perkembangan pelbagai kajian.

Boleh melayani anda: trapezoid segi empat tepat: sifat, hubungan dan formula, contoh

Di dalam fizikal Pemalar integrasi boleh mengambil pelbagai nilai mengikut sifat data. Contoh yang sangat biasa adalah mengetahui fungsi V (t) yang mewakili kelajuan zarah berbanding masa t. Diketahui bahawa apabila mengira v (t) primitif, fungsi diperolehi R (t) yang mewakili kedudukan zarah berbanding masa.

The Pemalar integrasi akan mewakili nilai kedudukan awal, iaitu pada masa ini t = 0.

Begitu juga, jika fungsi itu diketahui A (t)  yang mewakili pecutan zarah berbanding masa. Primitif a (t) akan menghasilkan fungsi v (t), di mana Pemalar integrasi Ia akan menjadi nilai halaju awal v₀.

Di dalam ekonomi, dengan mendapatkan primitif fungsi kos dengan integrasi. The Pemalar integrasi akan mewakili kos tetap. Dan begitu banyak aplikasi lain yang merit pembezaan dan kalkulus integral.

Bagaimana integrasi tetap dikira?

Untuk pengiraan Pemalar integrasi, Selalu perlu untuk mengetahui keadaan awal. Yang bertanggungjawab untuk menentukan yang mana primitif yang mungkin adalah yang sepadan.

Dalam banyak aplikasi, ia dianggap sebagai pemboleh ubah bebas ke masa (t), di mana pemalar C Ambil nilai yang menentukan keadaan awal kes tertentu.

Jika contoh awal diambil: ∫ (2x+1) dx = x² + x + C

Keadaan awal yang sah boleh untuk membuat grafik untuk melewati koordinat tertentu. Sebagai contoh, diketahui bahawa primitif (x² + x + C) Pergi melalui titik (1, 2)

F (x) = x² + x + C; Ini adalah penyelesaian umum

F (1) = 2

Kami menggantikan penyelesaian umum dalam kesamaan ini

F (1) = (1)² + (1) + c = 2

Di mana ia mudah disimpulkan C = 0

Dengan cara ini primitif yang sepadan untuk kes ini adalah F (x) = x² + x

Terdapat pelbagai jenis latihan berangka yang berfungsi dengan Pemalar integrasi. Malah, kalkulus perbezaan dan integral tidak berhenti digunakan dalam siasatan semasa. Pada tahap akademik yang berbeza, anda dapat mencari; Dari pengiraan awal, melalui fizik, kimia, biologi, ekonomi, antara lain.

Ia juga dihargai dalam kajian persamaan pembezaan, Dimanakah Pemalar integrasi Anda boleh mengambil pelbagai nilai dan penyelesaian, ini disebabkan oleh pelbagai rujukan dan integrasi yang dijalankan dalam perkara ini.

Contoh

Contoh 1

1. Meriam terletak 30 meter pucuk tinggi secara menegak sehingga peluru. Diketahui bahawa kelajuan peluru awal adalah 25 m/s. Tentukan:

• Fungsi yang mentakrifkan kedudukan peluru berkenaan dengan masa.
• Masa penerbangan atau masa di mana zarah memainkan tanah.

Ia boleh melayani anda: 8 jenis kesilapan pengukuran (dengan contoh)

Diketahui bahawa dalam pecutan pergerakan rectilinear yang bervariasi adalah nilai malar. Ini adalah kes pelancaran peluru, di mana pecutan akan menjadi graviti

G = - 10 m/s²

Ia juga diketahui bahawa pecutan adalah yang kedua yang diperoleh dari kedudukan, menunjukkan integrasi berganda ke dalam resolusi latihan, sehingga memperoleh dua Pemalar integrasi.

A (t) = -10

V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C₁

Keadaan awal latihan menunjukkan bahawa kelajuan awal adalah v₀ = 25 m/s. Ini adalah kelajuan pada masa t = 0. Dengan cara ini ia dipenuhi bahawa:

V (0) = 25 = -10 (0) + C₁   dan C₁ = 25

Fungsi kelajuan ditakrifkan

V (t) = -10t + 25; Anda dapat melihat persamaan dengan formula MRUV (v_F = V₀ + A X T)

Dalam homolog, fungsi kelajuan disepadukan untuk mencapai ungkapan yang mentakrifkan kedudukan:

R (t) = ∫v (t) dt = ∫ (-10t+25) dt = -5t² + 25t + C₂

R (t) = -5t² + 25t + C₂  (Kedudukan primitif)

Kedudukan awal r (0) = 30 m diketahui. Kemudian primitif tertentu peluru dikira.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Di mana C₂ = 30

Bahagian pertama diselesaikan sejak itu R (t) = -5t² + 25t + 30  ; Ekspresi ini adalah homolog dari formula anjakan dalam MRUV r (t) = r₀ + V₀T - gt²/2

Untuk bahagian kedua persamaan kuadratik mesti diselesaikan: -5t² + 25t + 30 = 0

Oleh kerana ia keadaan zarah untuk mencapai tanah (kedudukan = 0)

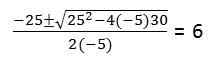Sumber: Pengarang

Sebenarnya persamaan gred ke -2 melemparkan 2 penyelesaian t: 6, -1. Nilai t = -1 diabaikan kerana ini adalah unit masa yang domainnya tidak termasuk nombor negatif.

Dengan cara ini bahagian kedua di mana masa penerbangan bersamaan dengan 6 saat diselesaikan.

Contoh 2

2. Cari primitif F (x) yang memenuhi syarat awal:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Dengan maklumat derivatif kedua f "(x) = 4 proses antiderivasi bermula

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Kemudian, mengetahui keadaan f '(2) = 2 hasil:

4 (2) + c₁ = 2

C₁ = -6 dan f '(x) = 4x - 8

Teruskan dengan cara yang sama untuk yang kedua Pemalar integrasi

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Keadaan awal f (0) = 7 diketahui dan teruskan:

2 (0)² - 8 (0) + c₂ = 7

C₂ = 7 dan f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Sama dengan masalah sebelumnya kita menentukan derivatif pertama dan fungsi asal dari keadaan awal.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + c₁

Dengan keadaan f '(0) = 6 hasil:

Boleh melayani anda: Tetapkan Teori: Ciri, Elemen, Contoh, Latihan

(0³/3) + c₁ = 6; Di mana₁ = 6 dan f '(x) = (x³/3) + 6

Kemudian yang kedua Pemalar integrasi

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Keadaan awal f (0) = 3 diketahui dan teruskan:

[(0)⁴/12] + 6 (0) + c₂ = 3; Di mana₂ = 3

Primitif tertentu diperoleh

f (x) = (x⁴/12) + 6x + 3

Contoh 3

3. Tentukan fungsi primitif yang diberikan derivatif dan titik graf:

• dy/dx = 2x - 2 yang melewati titik (3, 2)

Penting untuk diingat bahawa derivatif merujuk kepada cerun garis tangen ke lengkung pada titik tertentu. Di mana tidak betul untuk menganggap bahawa grafik derivatif menyentuh titik yang ditunjukkan, kerana ia tergolong dalam graf fungsi primitif.

Dengan cara ini kita menyatakan persamaan pembezaan seperti berikut:

dy = (2x - 2) dx  ; Kemudian apabila menggunakan kriteria antiderivasi yang anda ada:

∫dy = ∫ (2x - 2) dx

y = x² - 2x + c

Memohon keadaan awal:

2 = (3)² - 2 (3) + c

C = -1

Diperoleh: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1 yang melalui titik (0, 2)

Kami menyatakan persamaan pembezaan seperti berikut:

dy = (3x² - 1) dx  ; Kemudian apabila menggunakan kriteria antiderivasi yang anda ada:

 ∫dy = ∫ (3x² - 1) dx

y = x³ - x + c

Memohon keadaan awal:

2 = (0)² - 2 (0) + c

C = 2

Diperoleh: f (x) = x³ - x + 2

Latihan yang dicadangkan

Latihan 1

1. Cari primitif F (x) yang memenuhi syarat awal:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Latihan 2

2. Belon yang naik dengan kelajuan 16 kaki/s melepaskan jaket pasir dari ketinggian 64 kaki di atas paras tanah.

• Tentukan masa penerbangan
• Apa yang akan menjadi vektor v_F Apabila anda menyentuh lantai?

Latihan 3

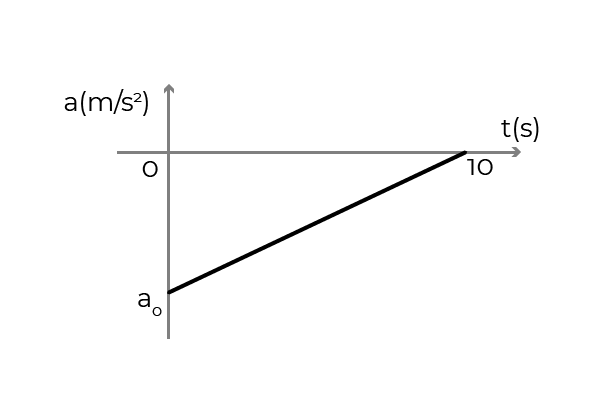
3. Angka ini menunjukkan graf pecutan - masa kereta yang bergerak dalam erti positif paksi x. Kereta itu bergerak ke kelajuan berterusan 54 km/j ketika pemandu memohon brek untuk berhenti dalam 10 saat. Tentukan:

• Pecutan awal kereta
• Kelajuan kereta pada t = 5s
• Anjakan kereta semasa brek

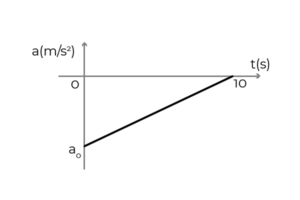Sumber: Pengarang

Latihan 4

4. Tentukan fungsi primitif yang diberikan derivatif dan titik graf:

• dy/dx = x yang melewati titik (-1, 4)
• dy/dx = -x² + 1 yang melalui titik (0, 0)
• dy/dx = -x + 1 yang melewati titik (-2, 2)

Rujukan

1. Kalkulus integral. Kaedah integral dan integrasi yang tidak ditentukan. Wilson, Velásquez Bastidas. Universiti Magdalena 2014
2. Stewart, J. (2001). Pengiraan pemboleh ubah. Transenden awal. Mexico: Thomson belajar.
3. Jiménez, r. (2011). Matematik vi. Kalkulus integral. Mexico: Pendidikan Pearson.
4. Fizik i. MC Graw Hill