Perpaduan Perpaduan Apa, Pengiraan, Latihan

The pemalar proporsional Ia adalah elemen berangka hubungan, digunakan untuk menentukan corak persamaan antara 2 magnitud yang diubah secara serentak. Sangat biasa untuk mewakilinya sebagai fungsi linear generik melalui ekspresi f (x) = k.X. Walau bagaimanapun, ini bukan satu -satunya perwakilan yang mungkin berkadar.

Contohnya, hubungan antara x dan y dalam fungsi y = 3x mempunyai perkadaran yang tetap sama dengan 3. Ia menunjukkan bahawa apabila pembolehubah bebas x tumbuh, begitu pula pemboleh ubah bergantung dan, dalam tiga nilai sebelumnya.

Perubahan yang digunakan dalam satu pemboleh ubah, mempunyai kesan segera di pihak yang lain, sehingga ada nilai yang dikenali sebagai pemalar yang berkadar. Ini berfungsi untuk mengaitkan magnitud yang berbeza yang kedua -dua pembolehubah memperoleh.

[TOC]

Berapakah perkadaran dan jenis yang berterusan

Menurut trend dalam mengubah pembolehubah, berkadar dapat diklasifikasikan kepada 2 jenis.

Perkadaran langsung

Mencadangkan hubungan satu arah antara dua magnitud. Di dalamnya, jika pemboleh ubah bebas membentangkan beberapa pertumbuhan, pemboleh ubah bergantung juga akan berkembang. Begitu juga, penurunan dalam pemboleh ubah bebas akan menyebabkan penurunan magnitud dan.

Sebagai contoh, fungsi linear yang digunakan dalam pengenalan; Y = 3x, sepadan dengan nisbah langsung yang berkadar. Ini kerana peningkatan pembolehubah bebas x akan menyebabkan peningkatan tiga kali ganda dalam nilai sebelumnya yang diambil oleh pemboleh ubah bergantung dan.

Begitu juga, pemboleh ubah bergantung akan mengurangkan tiga kali ganda nilainya apabila x turun magnitud.

Nilai pemalar berkadar "k" dalam hubungan langsung ditakrifkan sebagai k = y/x.

Perkadaran songsang atau tidak langsung

Dalam jenis fungsi ini, hubungan antara pembolehubah dibentangkan dengan cara antonim, di mana pertumbuhan atau penurunan pembolehubah bebas masing -masing sepadan dengan penurunan atau pertumbuhan pemboleh ubah bergantung.

Ia dapat melayani anda: penguraian nombor semula jadi (contoh dan latihan)

Sebagai contoh, fungsi f (x) = k/x adalah hubungan songsang atau tidak langsung. Oleh kerana nilai pemboleh ubah bebas mula meningkat, nilai k akan dibahagikan dengan angka yang semakin meningkat, menjadikan penurunan nilai yang bergantung kepada nilai mengikut perkadaran.

Mengikut nilai yang diambil oleh K, kecenderungan fungsi songsang berkadar dapat ditakrifkan. Sekiranya k> 0, maka fungsi akan berkurangan dalam semua nombor sebenar. Dan grafnya akan terletak di kuadran pertama dan ke -3.

Sebaliknya, jika nilai k adalah negatif atau kurang daripada sifar, fungsi akan meningkat dan grafnya akan dijumpai di kuadran ke -2 dan 4.

Bagaimana ia dikira?

Terdapat konteks yang berbeza di mana definisi pemalar perkadaran mungkin diperlukan. Dalam kes yang berbeza, data yang berbeza mengenai masalah akan ditunjukkan, di mana kajian ini akhirnya akan menunjukkan nilai k.

Dengan cara generik, yang disebutkan di atas boleh direkodkan semula. Nilai k sesuai dengan dua ungkapan mengikut jenis perkadaran yang hadir:

- Langsung: k = y/x

- Songsang atau tidak langsung: k = y.X

Menurut graf anda

Kadang -kadang hanya graf fungsi yang akan diketahui sebahagian atau sepenuhnya. Dalam kes ini, perlu, dengan analisis grafik, tentukan jenis perkadaran. Maka kita perlu menentukan koordinat yang membolehkan untuk mengesahkan nilai x dan y untuk memohon kepada formula k yang sepadan.

Grafik yang merujuk kepada berkadar langsung adalah jenis linear. Sebaliknya, graf fungsi berkadar songsang biasanya membentuk hiperbola.

Menurut Jadual Nilai

Dalam sesetengah kes terdapat jadual nilai dengan nilai yang sepadan dengan setiap lelaran pemboleh ubah bebas. Biasanya ini menunjukkan kesedaran graf selain menentukan nilai k.

Boleh melayani anda: Pengagihan Kekerapan: Cara Membuat Jadual, Contoh, Latihan

Menurut ungkapan analisis

Menunjukkan ungkapan yang mentakrifkan secara analitik. Secara langsung nilai k dapat jelas, atau ia juga dapat disimpulkan dari ungkapan itu sendiri.

Sebagai peraturan tiga langsung atau sebatian

Dalam model senaman lain terdapat data tertentu, yang merujuk kepada hubungan antara nilai. Ini diperlukan untuk permohonan tiga langsung atau kompaun untuk menentukan data yang diperlukan pada tahun ini.

Sejarah

Konsep perkadaran selalu ada. Bukan sahaja dalam fikiran dan kerja ahli matematik yang hebat, tetapi dalam kehidupan seharian penduduk, kerana kepraktisan dan kebolehgunaannya.

Sangat biasa untuk memenuhi situasi yang memerlukan pendekatan berkadar. Ini dibentangkan dalam setiap kes di mana pembolehubah dan fenomena dibandingkan yang menjaga hubungan tertentu.

Melalui garis masa kita dapat mencirikan momen sejarah, di mana kemajuan matematik mengenai perkadaran telah digunakan.

- Abad kedua a.c. Sistem penyimpanan pecahan dan perkadaran di Greece diterima pakai.

- Abad ke -5 a.c. Perkadaran yang berkaitan dengan sisi dan pepenjuru persegi juga ditemui di Greece.

- 600 a.c. Tales de Mileto membentangkan teoremnya mengenai perkadaran.

- Tahun 900. Sistem perpuluhan yang sebelum ini digunakan oleh India atas alasan dan perkadaran dilanjutkan. Sumbangan yang dibuat oleh orang Arab.

- XVII Abad. Sumbangan merujuk kepada perkadaran dalam pengiraan Euler tiba.

- XIX Century. Gauss menyediakan konsep bilangan dan perkadaran yang kompleks.

- Abad kedua puluh. Perkadaran sebagai model fungsi ditakrifkan oleh gula dan deulofeo.

Latihan yang diselesaikan

Latihan 1

Ia dikehendaki mengira nilai pembolehubah x, y, z dan g. Mengetahui hubungan berkadar berikut:

3x + 2y - 6z + 8g = 1925

Boleh melayani anda: Pemboleh ubah rawak berterusan

x/3 = y/8 = z/3 = g/5

Nilai relatif pemalar perkadaran ditakrifkan. Ini dapat diperoleh dari hubungan kedua, di mana nilai yang membahagikan setiap pembolehubah menunjukkan hubungan atau alasan mengenai k.

X = 3k y = 2k z = 3k g = 5k

Nilai digantikan dalam ungkapan pertama, di mana sistem baru akan dinilai dalam pemboleh ubah k tunggal.

3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925

9k + 4k -18k + 40k = 1925

35k = 1925

K = 1925/35 = 55

Menggunakan nilai ini pemalar perkadaran kita dapat mencari angka yang mentakrifkan setiap pembolehubah.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Latihan 2

Kirakan pemalar perkadaran dan ungkapan yang mentakrifkan fungsi, memandangkan grafiknya.

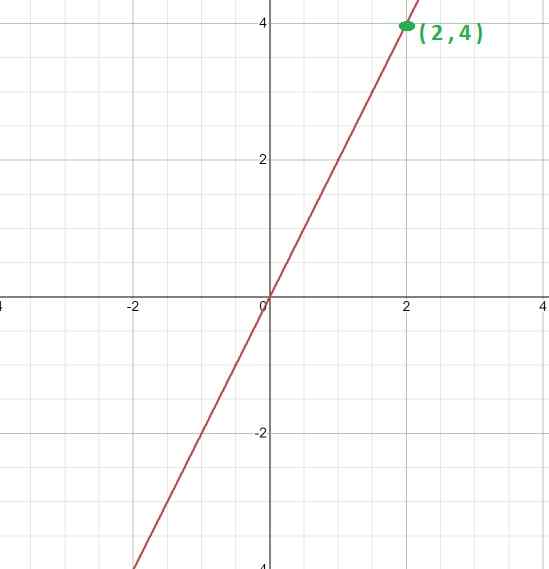
Pertama, graf dianalisis, watak linearnya jelas. Ini menunjukkan bahawa ia adalah fungsi dengan perkadaran langsung dan nilai k akan diperolehi melalui ungkapan k = y/x

Maka titik graf yang boleh ditentukan dipilih, iaitu, satu di mana koordinat yang mengarangnya boleh tepat.

Untuk kes ini titik diambil (2, 4). Di mana kita boleh menjalin hubungan berikut.

K = 4/2 = 2

Supaya ungkapan ditakrifkan oleh fungsi y = kx, yang untuk kes ini akan

F (x) = 2x

Rujukan

1. Matematik untuk Elektrik & Elektronik. Dr. Arthur Kramer. Pembelajaran Cengage, 27 Julai. 2012
2. Visi 2020: Peranan Strategik Penyelidikan Operasi. N. Ravichandran. Penerbit Sekutu, 11 Sept. 2005
3. Pengetahuan Tatabahasa dan Aritmetik Pembantu Pentadbiran Negeri.e-book. Mad-eduform
4. MATEMATIK KEPUTUSAN UNTUK SOKONGAN DAN PENGURUSAN Kurikulum: Untuk sokongan dan kepelbagaian kurikulum. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29 Ogos. 2003
5. Logistik dan pengurusan komersial. Maria José Escudero Serrano. Edisi Paraninfo, s.Ke., 1 Sept. 2013