Laman utama
Matematik
Decagon biasa, tidak teratur, sifat, contoh

Matematik

Decagon biasa, tidak teratur, sifat, contoh

3012
40
Delbert Dare

Dia decagon Ia adalah angka rata dengan poligon berbentuk 10 sisi dan 10 simpang atau petua. The Decagons boleh menjadi biasa atau tidak teratur, dalam kes pertama semua sisi dan sudut dalaman mempunyai ukuran yang sama, sementara di kedua sisi dan/atau sudut berbeza antara satu sama lain.

Rajah 1 menunjukkan contoh dekagon setiap jenis dan seperti yang dapat kita lihat, decagon biasa sangat simetris.

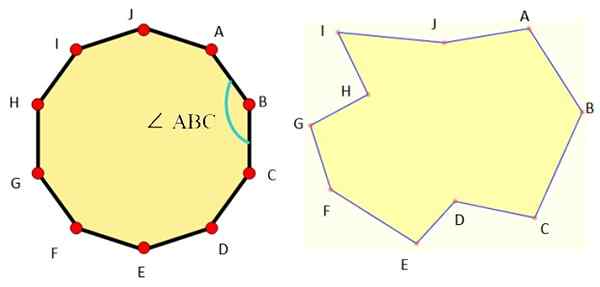Rajah 1. Ke kiri decagon biasa dan di sebelah kanan decagon yang tidak teratur. Sumber: Wikimedia Commons/F. Zapata/Mathpenref.

Unsur -unsur asas semua decagon adalah:

-Sisi, segmen garis yang ketika menyertai decagon.

-Simpang, atau titik di antara setiap sisi berturut -turut.

-Sudut dalaman dan luaran antara sisi bersebelahan.

-Pepenjuru, segmen yang menyatukan dua simpang bukan berturut -turut.

Tangkai dipanggil oleh huruf besar, seperti yang ditunjukkan dalam Rajah 1, di mana huruf pertama abjad digunakan, tetapi surat boleh digunakan.

Sisi dilambangkan dengan dua huruf dari simpang di antaranya, contohnya sisi ab adalah antara simpang a dan b. Dengan cara yang sama ia dilakukan dengan pepenjuru, jadi kami mempunyai AF pepenjuru, yang menyertai mata a dan f.

Untuk sudut kita menggunakan simbol ini: ∠, sama dengan l cenderung l. Contohnya, sudut ∠ ABC adalah salah satu puncaknya B dan bahagiannya adalah segmen AB dan BC.

[TOC]

Decagon biasa

Dalam decagon biasa, semua pihak mempunyai ukuran yang sama, serta sudut dalaman. Oleh itu dikatakan sebagai sama (sisi yang sama) dan equiangular (Sudut sama). Ia adalah angka yang sangat simetri

Sudut dalaman decagon biasa

Untuk mencari ukuran sudut dalaman poligon biasa, termasuk decagon biasa, formula berikut digunakan:

$I=\frac(n-2)\times 180^^on$

Di mana:

-Saya adalah ukuran sudut dalam darjah.

-n adalah bilangan sisi poligon. Sekiranya berlaku decagon n = 10.

Boleh melayani anda: heptagon

Menggantikan n = 10 dalam formula sebelumnya kita memperoleh yang berikut:

$I=\frac(10-2)\times 180^^o10=144^^o$

Sekarang, dikatakan bahawa poligon adalah cembung Sekiranya langkah sudutnya kurang daripada 180º, jika tidak, poligon adalah cekung. Seperti mana -mana sudut dalaman decagon biasa mengukur 144º dan kurang daripada 180º, maka ia adalah poligon cembung.

Jumlah sudut dalaman

Jumlah ukuran sudut dalaman mana -mana poligon adalah, dalam darjah:

S = (n-2) x 180º; n selalu lebih besar daripada 2

Dalam formula ini kita perlu:

-S adalah jumlah ukuran sudut dalaman.

-n adalah bilangan sisi. Untuk decagon n = 10

Memohon formula untuk n = 10 hasil:

S = (10 - 2) x 180º = 1440º

Sudut luaran

Sudut luar dibentuk di antara satu sisi dan lanjutan sebelah bersebelahan, mari kita lihat:

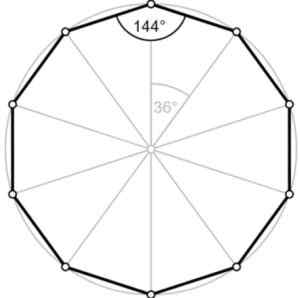
Rajah 2.- Sudut luaran decagon biasa berukuran 36º. Fountain. Wikimedia Commons/F. Zapata.

Sudut ∠ ABC ditambah sudut luaran menambah 180º, iaitu, mereka Tambahan. Oleh itu sudut luaran adalah sama dengan 180º-144º = 36º, seperti yang kita lihat dalam angka itu.

Bilangan pepenjuru

Seperti yang dinyatakan sebelum ini, pepenjuru adalah segmen yang menyatukan simpang. Berapa banyak pepenjuru yang dapat kita jejak dalam satu decagon? Apabila bilangan simpang kecil, mereka dapat dengan mudah dikira, tetapi apabila jumlah itu meningkat, anda boleh kehilangan akaun.

Nasib baik ada formula untuk mengetahui jumlah pepenjuru yang dimiliki oleh poligon n Sisi:

$D=\fracn(n-3)2$

Untuk decagon kita menggantikan n = 10 dan dapatkan:

D = 10 x (10 - 3) /2 = 35

Dalam decagon biasa, semua pepenjuru dipotong pada satu titik, yang merupakan pusat angka:

Rajah 3. Sudut dan pepenjuru decagon biasa. Sumber: Wikimedia Commons.

Pusat

Pusat poligon ditakrifkan sebagai titik yang sama dari mana -mana puncak. Dalam angka sebelumnya, pusat ini bertepatan dengan titik persimpangan semua pepenjuru.

Perimeter

Jika decagon biasa mempunyai sisi A, perimeter p adalah jumlah semua pihak:

Boleh melayani anda: 90 pembahagi: Apa dan penjelasan

P = 10.ke

Kawasan

Mengetahui panjangnya ke Di sisi lain, kawasan Decagon biasa dikira oleh:

$A=\left (\frac52 \right )cot\left ( \frac\pi 10 \right )a^2$

Formula anggaran untuk kawasan itu ialah:

$A=\frac10a^24 \times tg\left ( \frac\pi 10 \right )\simeq 7.694a^2$

Dan pilihan ketiga untuk mencari kawasan itu adalah dengan panjang apothem l_Ke. Ini adalah segmen yang bergabung dengan titik tengah di satu sisi dengan pusat poligon.

Dalam kes ini, kawasan ini boleh dikira menggunakan formula:

$A=\fracP.L__A2=\frac10a\times L_A2$

Decagon yang tidak teratur

Decagon yang tidak teratur tidak sama rata atau sama, dan secara umum ia tidak mempunyai simetri angka biasa, walaupun beberapa dekagon mungkin mempunyai paksi simetri.

Mereka juga boleh cembung atau cekung, jika terdapat sudut dalaman lebih besar daripada 180º.

Decagon yang tidak teratur Rajah 1 adalah cekung, kerana beberapa sudut dalamannya lebih besar daripada 180º. Jelas bahawa terdapat banyak kombinasi sudut dan sisi yang menimbulkan decagon yang tidak teratur.

Walau apa pun, ia dipenuhi bahawa:

-Sudut dalaman decagon yang tidak teratur juga menambah 1440º.

-Ia juga mempunyai 35 pepenjuru.

Kawasan decagon yang tidak teratur oleh penentu gauss

Secara umum tidak ada formula yang unik untuk mencari kawasan poligon yang tidak teratur, kerana sisi dan sudut berbeza. Walau bagaimanapun, anda dapat mengetahui mengetahui koordinat simpang dan mengira Penentu Gauss:

-Mari kita hubungi (x_n , dan_n) kepada koordinat simpang, dengan n bervariasi dari 1 hingga 10.

-Anda boleh bermula dari mana -mana puncak, yang mana koordinat akan diberikan (x x₁, dan₁). Sekarang anda perlu mengganti nilai setiap koordinat dalam formula ini:

$A=\left |\frac(x_1y_2-x_2y_1)+(x_2y_3-x_3y_2)+(x_3y_4-x_4y_3)+… (x_ny_1-x_1y_n)2 \right |$

Di mana penentu adalah tepat operasi antara tanda kurung.

-Penting untuk diperhatikan bahawa penentu terakhir melibatkan puncak pertama bersama -sama dengan yang terakhir. Untuk Decagon, ia akan menjadi seperti ini:

(x₁₀dan₁ - x₁dan₁₀)

Boleh melayani anda: Interpolasi LaGrange

Penting: Bar adalah nilai mutlak dan bermaksud bahawa hasil akhir selalu dengan tanda positif.

Prosedur ini boleh menjadi susah payah apabila angka itu mempunyai banyak simpul, dalam hal decagon terdapat 10 operasi, jadi disarankan untuk membuat jadual atau senarai.

Latihan diselesaikan

Kirakan kawasan decagon yang tidak teratur yang ditunjukkan dalam angka. Koordinat simpang adalah A, B, C ... J, yang nilainya ditunjukkan di sebelah kiri.

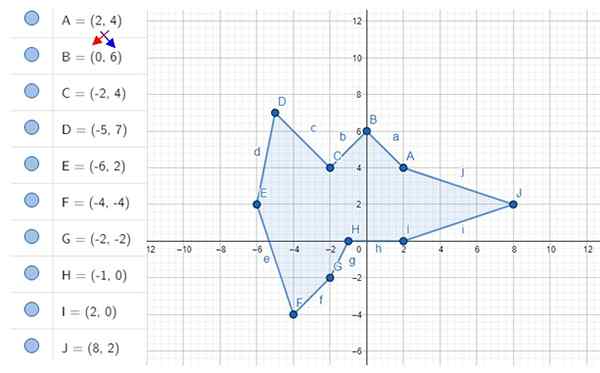Rajah 4. Decagon yang tidak teratur dan simpangnya. Sumber: f. Zapata dengan geogebra.

Penyelesaian

-Kami membuat setiap 10 operasi:

2 × 6 - 4 × 0 = 12 - 0 = 12
0 × 4 - 6 × (-2) = 0 + 12 = 12
(-2) × 7- 4 × (-5) = -14 + 20 = 6
(-5) × 2 -7 × (-6) = -10 + 42 = 32
(-6) × (-4) -2 × (-4) = 24 + 8 = 32
(-4) × (-2)-(-4) × (-2) = 8-8 = 0
(-2) × 0-(-2) × (-1) = 0 -2
(-1) × 0 - 0 × (2) = 0 - 0 = 0
2 × 2 - 0 × 8 = 4 - 0 = 4
8 × 4 -2 × 2 = 32 - 4 = 28

-Kami menambah hasilnya:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Hasil positif diperoleh walaupun tanpa bar nilai mutlak, tetapi jika negatif, yang sama berubah.

-Hasil sebelumnya dibahagikan dengan 2 dan itu adalah kawasan poligon:

A = 124/2 = 62

Sifat decangon

Berikut adalah ringkasan sifat umum decagon, sama ada biasa atau tidak teratur:

-Mempunyai 10 sisi dan 10 simpul.

-Jumlah sudut dalaman ialah 1440º.

-Terdapat 35 pepenjuru.

-Perimeter adalah jumlah semua pihak.

-Anda boleh membuat segitiga di dalam segmen lukisan poligon dari puncak kepada orang lain. Dalam satu decagon adalah mungkin untuk menarik 8 segitiga dengan cara ini, seperti yang ditunjukkan di bawah:

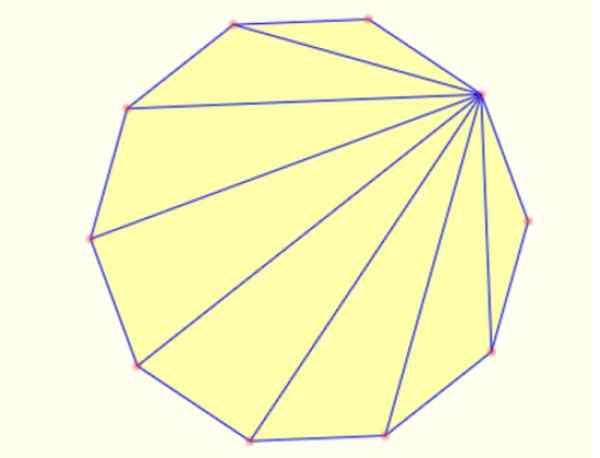Rajah 5. Segitiga dalaman dalam decagon biasa. Sumber: Mathpenref.

Rujukan

Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
Decagon.com. Decagon. Pulih dari: decagon.com
Rujukan terbuka matematik. Decagon. Pulih dari: Mathpenref.com.
Matematik Sangaku. Unsur poligon dan klasifikasinya. Pulih dari: Sangakoo.com.
Wikipedia. Decagon. Pulih dari: Adakah.Wikipedia.com.