Derivatif algebra

Apakah derivatif algebra?

The derivatif algebra Mereka terdiri daripada kajian terbitan dalam kes tertentu fungsi algebra. Asal pengertian tarikh derivatif kembali ke Yunani kuno. Perkembangan tanggapan ini didorong oleh keperluan untuk menyelesaikan dua masalah penting, satu dalam fizik dan satu dalam matematik.

Dalam fizik, derivatif menyelesaikan masalah menentukan kelajuan seketika objek bergerak. Dalam matematik, ia membolehkan untuk mencari garis tangen ke lengkung pada titik tertentu.

Walaupun terdapat banyak lagi masalah yang diselesaikan dengan menggunakan derivatif, serta generalisasinya, hasil yang datang kemudian untuk pengenalan konsep mereka.

Perintis kalkulus pembezaan adalah Newton dan Leibniz. Sebelum memberikan definisi rasmi, kami akan mengembangkan idea di belakang, dari pandangan matematik dan fizikal.

Derivatif sebagai sementara menunggu garis tangen ke lengkung

Katakan graf fungsi y = f (x) adalah graf berterusan (tanpa pancang atau simpang atau pemisahan), dan sama ada a = (a, f (a)) titik tetap di atasnya. Kami ingin mencari persamaan garis tangen ke fungsi f pada titik a.

Mari kita ambil titik lain p = (x, f (x)) graf, dekat dengan titik A, dan mengesan garis pengeringan yang melalui A dan P. Garis pengeringan adalah garis yang memotong graf lengkung menjadi satu atau lebih mata.

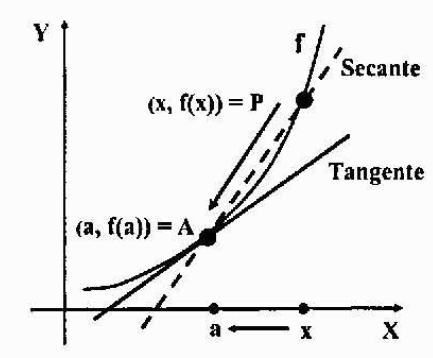
Untuk mendapatkan garis tangen yang kita mahukan, hanya perlu untuk mengira cerun kerana kita sudah mempunyai titik garis: titik a.

Sekiranya kita menggerakkan titik P oleh graf dan kita mendekati lebih banyak lagi ke arah A, garis kering yang disebutkan sebelumnya akan mendekati garis tangen yang anda ingin cari. Mengambil had apabila "P cenderung kepada", kedua -dua baris akan bertepatan, oleh itu lereng mereka juga.

Cerun garis secant diberikan oleh

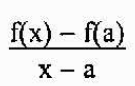
Untuk mengatakan bahawa P adalah dekat dengan A, bersamaan dengan mengatakan bahawa "x" mendekati "a". Oleh itu, cerun garis tangen ke graf F pada titik A akan sama dengan:

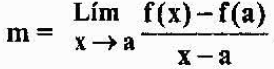
Ungkapan sebelumnya dilambangkan oleh f '(a), dan ditakrifkan sebagai terbitan fungsi f pada titik "a". Kami melihat bahawa secara analitik, derivatif fungsi pada satu titik adalah had, tetapi secara geometri, ia adalah cerun garis tangen ke carta fungsi pada titik.

Boleh melayani anda: pemboleh ubah rawak: konsep, jenis, contoh

Sekarang kita akan melihat tanggapan ini dari sudut pandangan fizik. Kami akan mencapai ekspresi yang sama dari had sebelumnya, walaupun dengan jalan yang berbeza, dengan itu memperoleh kesepakatan definisi.

Derivatif sebagai kelajuan seketika objek bergerak

Mari kita lihat contoh ringkas mengenai kelajuan seketika apa. Apabila dikatakan, sebagai contoh, kereta untuk mencapai destinasi melakukannya dengan kelajuan 100 km sejam, apa maksudnya ialah dalam satu jam dia mengembara 100 km.

Ini tidak semestinya bermaksud bahawa sepanjang jam kereta itu selalu 100 km, vecimeter kereta dapat dalam beberapa saat menandakan kurang atau lebih. Sekiranya dia mempunyai keperluan untuk berdiri di lampu isyarat, kelajuan pada masa itu adalah 0 km. Walau bagaimanapun, selepas satu jam, laluan itu 100 km.

Inilah yang dikenali sebagai kelajuan purata dan diberikan oleh jarak jauh perjalanan antara masa berlalu, seperti yang baru saja kita lihat. Sementara itu, kelajuan seketika, adalah yang menandakan jarum velocimeter sebuah kereta pada waktu tertentu (masa).

Mari kita lihat ini sekarang dengan cara yang lebih umum. Katakan bahawa objek bergerak di sepanjang garis dan bahawa anjakan ini diwakili dengan cara persamaan s = f (t), di mana pembolehubah t mengukur masa dan pembolehubah s anjakan, dengan mengambil kira permulaannya pada masa t = 0, pada masa itu juga sifar, iaitu, f (0) = 0.

Fungsi ini f (t) dikenali sebagai fungsi kedudukan.

Ungkapan untuk kelajuan seketika objek dicari pada waktu tetap. Pada kelajuan ini kita akan menunjukkannya dengan v (a).

Sama ada seketika hampir "A". Dalam selang masa antara "a" dan "t", perubahan kedudukan diberikan oleh f (t) -f (a).

Kelajuan purata dalam selang masa ini ialah:

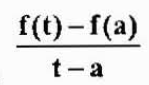
Yang merupakan penghampiran kelajuan seketika v (a). Pendekatan ini akan lebih baik kerana T semakin dekat dengan "A". Oleh itu,

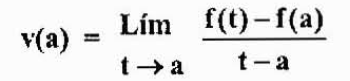
Mari kita perhatikan bahawa ungkapan ini sama dengan yang diperolehi dalam kes sebelumnya, tetapi dari perspektif yang berbeza. Inilah yang dikenali sebagai derivatif fungsi f pada titik "a" dan dilambangkan oleh f '(a), seperti yang dinyatakan di atas.

Boleh melayani anda: Undang -undang eksponen

Perhatikan bahawa membuat perubahan h

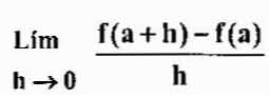
Kedua -dua ungkapan itu bersamaan tetapi kadang -kadang ia harus digunakan lebih kepada satu daripada yang lain, bergantung pada kes itu.

Ia kemudiannya ditakrifkan lebih umum yang diperoleh dari fungsi f pada bila -bila masa "x" milik domainnya sebagai

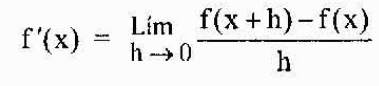
Notasi yang paling biasa untuk mewakili derivatif fungsi y = f (x) adalah yang baru kita lihat (f 'o y'). Walau bagaimanapun, satu lagi notasi yang digunakan secara meluas ialah notasi Leibniz yang diwakili sebagai mana -mana ungkapan berikut:

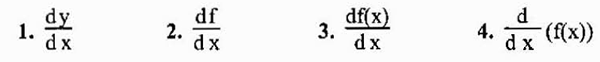
Memandangkan hakikat bahawa derivatif pada dasarnya adalah had, mungkin atau tidak mungkin wujud, kerana had tidak selalu ada. Sekiranya ia wujud, dikatakan bahawa fungsi yang dipersoalkan adalah berbeza pada titik tertentu.

Fungsi algebra

Fungsi algebra adalah gabungan polinomial melalui jumlah, penolakan, produk, kuota, kuasa dan radikal.

Polinomial adalah ungkapan bentuk

P_n= a_nxⁿ+ ke_N-1x^N-1+ ke_N-2x^N-2+... + a₂x²+ ke₁x+a₀

Di mana n adalah nombor semula jadi dan semua_Yo, Dengan i = 0.1, ..., n adalah nombor rasional dan_n≠ 0. Dalam kes ini dikatakan bahawa tahap polinomial ini adalah n.

Berikut adalah contoh fungsi algebra:

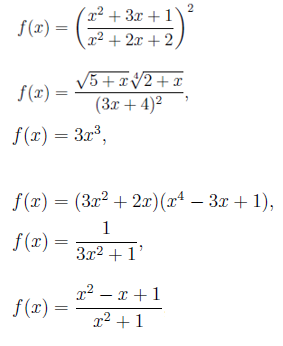
Di sini fungsi eksponen, logaritma dan trigonometri tidak termasuk. Peraturan terbitan yang akan kita lihat di bawah adalah sah untuk fungsi secara umum, tetapi kita akan menyekat dan menerapkannya dalam hal fungsi algebra.

Peraturan Derrying

Berasal dari yang berterusan

Menyatakan bahawa terbitan pemalar adalah sifar. Iaitu, jika f (x) = c, maka f '(x) = 0. Sebagai contoh, derivatif fungsi malar 2 adalah sama dengan 0.

Berasal dari kuasa

Jika f (x) = xⁿ, maka f '(x) = nx^N-1. Contohnya, derivatif x³ Ia adalah 3x². Akibatnya, diperolehi yang diperoleh dari fungsi identiti f (x) = x adalah f '(x) = 1x^1-1= x⁰= 1.

Contoh lain adalah seperti berikut: Biarkan f (x) = 1/x², Kemudian f (x) = x^-2 dan f '(x) = -2x^-2-1= -2x^-3.

Harta ini juga akar yang sah, kerana akarnya adalah kuasa rasional dan di atas juga boleh digunakan dalam kes itu. Contohnya, yang diperoleh dari akar persegi diberikan oleh

Ia dapat melayani anda: anggaran mengikut selang waktu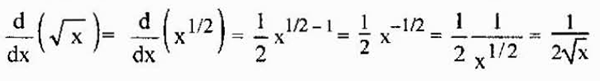

Berasal dari jumlah dan penolakan

Jika F dan G adalah fungsi yang boleh dibezakan dalam x, maka jumlah F+G juga dan ia dipenuhi bahawa (f+g) '(x) = f' (x)+g '(x) (x) (x).

Begitu juga anda perlu (f -g) '(x) = f' (x) -g '(x). Dalam erti kata lain, terbitan jumlah (penolakan) adalah jumlah (atau penolakan) derivatif.

Contoh

Jika h (x) = x²+X-1, kemudian

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produk yang diperoleh daripada produk

Sekiranya F dan G adalah fungsi yang boleh dibezakan dalam x, maka produk FG juga boleh dibezakan dalam x dan ia dipenuhi

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Akibatnya, jika C adalah tetap dan f adalah fungsi yang boleh dibezakan dalam x, maka cf juga boleh dibezakan dalam x y (cf) '(x) = cf' (x).

Contoh

Jika f (x) = 3x (x²+1) Kemudian

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Berasal dari kota

Jika F dan G dibezakan dalam x dan g (x) ≠ 0, maka f/g juga boleh dibezakan dalam x, dan ia dipenuhi

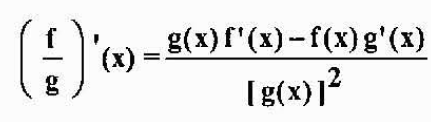
Contoh: Jika h (x) = x³/(x²-5x), kemudian

H '(x) = [(x³) '(X⁵-5x)-(x³) (x⁵-5x) ']/ (x⁵-5x)²= [(3x²) (x⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Peraturan rantai

Peraturan ini membolehkan untuk memperoleh komposisi fungsi. Ia menetapkan yang berikut: Jika y = f (u) dibezakan dalam u, dan u = g (x) boleh dibezakan dalam x, maka fungsi kompaun f (g (x)) adalah berbeza dalam x, dan ia dipenuhi [F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (X))] '= f' (g (x)) g '(x).

Iaitu, derivatif fungsi kompaun adalah hasil derivatif fungsi luaran (derivatif luaran) oleh fungsi dalaman yang diperolehi (derivatif dalaman).

Contoh

Jika f (x) = (x⁴-2x)³, Jadi

f '(x) = 3 (x⁴-2x)²(x⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Terdapat juga hasil untuk mengira derivatif converse fungsi, serta penyebaran kepada derivatif pesanan yang lebih tinggi. Aplikasi adalah luas. Antaranya, keuntungan mereka dalam pengoptimuman dan fungsi minimum diserlahkan.

Rujukan

1. Alarcon, s., González, m., & Quintana, h. (2008). Kalkulus berlainan. ITM.
2. Cabrera, v. M. (1997). 4000 pengiraan. Progreso editorial.
3. Castaño, h. F. (2005). Matematik sebelum pengiraan. Universiti Medellin.
4. Eduardo, n. Ke. (2003). Pengenalan Pengiraan. Edisi Umbral.
5. Sumber, a. (2016). Matematik asas. Pengenalan Pengiraan. Lulu.com.
6. Purcell, e. J., Rigdon, s. Dan., & Varberg, D. Dan. (2007). Pengiraan. Pendidikan Pearson.
7. Saenz, j. (2005). Kalkulus berlainan (Kedua ed.). Barquisimeto: Hypotenusa.
8. Thomas, g. B., & Weir, m. D. (2006). Pengiraan: Beberapa pembolehubah. Pendidikan Pearson.