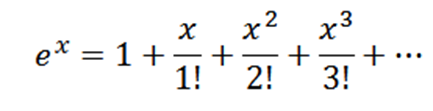Derivatif berturut -turut

Apa derivatif berturut -turut?

The derivatif berturut -turut Mereka adalah yang berasal dari fungsi selepas derivatif kedua. Proses untuk mengira derivatif berturut -turut adalah seperti berikut: Terdapat fungsi f, yang boleh kita dapatkan dan mendapatkan fungsi yang diperolehi f '. Untuk derivatif ini, kita dapat memperolehnya lagi, mendapatkan (f ')'.

Fungsi baru ini dipanggil derivatif kedua; Semua derivatif yang dikira dari yang kedua adalah berturut -turut; Ini, juga dipanggil perintah yang lebih tinggi, mempunyai aplikasi yang besar, seperti memberi maklumat mengenai strok graf fungsi, ujian derivatif kedua untuk hujung relatif dan penentuan siri tak terhingga.

Definisi

Menggunakan notasi Leibniz, kami mempunyai derivatif fungsi "y" berkenaan dengan "x" adalah dy/dx. Untuk menyatakan kepada derivatif kedua "Y" menggunakan notasi Leibniz, kami menulis seperti berikut:

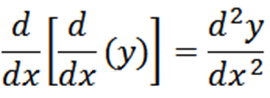
Secara umum, kita dapat menyatakan derivatif berturut -turut seperti berikut dengan notasi Leibniz, di mana n mewakili urutan derivatif.

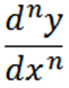
Notasi lain yang digunakan adalah seperti berikut:

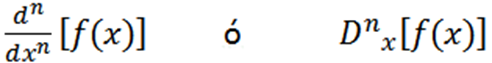
Beberapa contoh di mana kita dapat melihat notasi yang berbeza adalah:

Contoh 1

Dapatkan semua derivatif fungsi F yang ditakrifkan oleh:

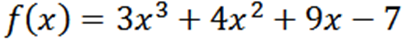
Menggunakan teknik rujukan biasa, kita mempunyai F ialah:

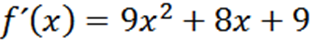
Mengulangi proses kita dapat memperoleh derivatif kedua, derivatif ketiga dan sebagainya.

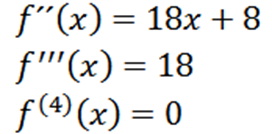
Perhatikan bahawa derivatif keempat adalah sifar dan derivatif sifar adalah sifar, jadi kita perlu:

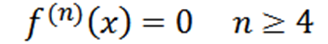
Contoh 2

Kirakan keempat yang diperoleh dari fungsi berikut:

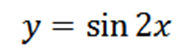
Memperoleh fungsi yang diberikan sebagai hasilnya:

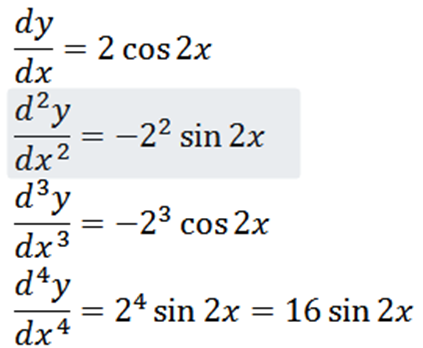
Kelajuan dan pecutan

Salah satu motivasi yang membawa kepada penemuan derivatif adalah mencari definisi kelajuan segera. Takrif rasmi adalah seperti berikut:

Boleh melayani anda: Nombor Primo: Ciri, Contoh, Latihan

Biarkan Y = F (T) Fungsi yang grafnya menerangkan trajektori zarah dalam sekejap t, Kemudian kelajuannya pada sekejap t diberikan oleh:

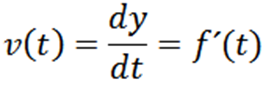
Sebaik sahaja kelajuan zarah diperoleh, kita dapat mengira pecutan segera, yang ditakrifkan seperti berikut:

Percepatan seketika zarah yang trajektori diberikan oleh y = f (t) adalah:

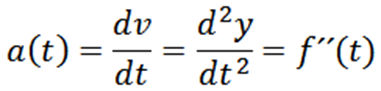
Contoh 1

Zarah bergerak pada garis mengikut fungsi kedudukan:

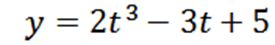
Di mana "y" diukur dalam meter dan "t" dalam beberapa saat.

• Pada masa apa kelajuan anda adalah 0?
• Pada masa apa pecutannya adalah 0?

Dengan memperoleh fungsi kedudukan "Y", kita mempunyai kelajuan dan percepatannya masing -masing oleh:

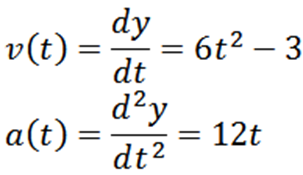
Untuk menjawab soalan pertama, sudah cukup untuk menentukan apabila fungsi V V adalah sifar; ini adalah:

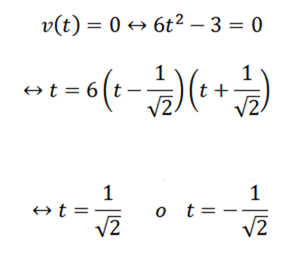
Kami meneruskan soalan seterusnya:

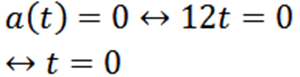
Contoh 2

Zarah bergerak pada garis mengikut persamaan pergerakan berikut:

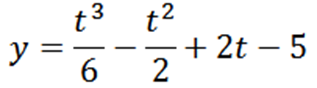
Tentukan "t, y" dan "v" apabila a = 0.

Mengetahui bahawa kelajuan dan percepatan diberikan oleh

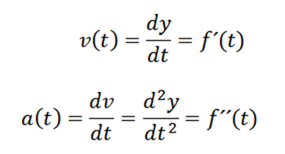
Kami terus memperoleh dan mendapatkan:

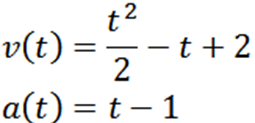
Melakukan a = 0, kita ada:

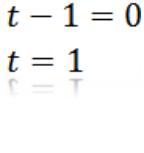
Di mana kita dapat menyimpulkan bahawa nilai t supaya A adalah sama dengan sifar adalah t = 1.

Kemudian, menilai dalam t = 1 fungsi kedudukan dan fungsi, kita perlu:

Aplikasi

Terbitan mplícita

Derivatif berturut -turut juga boleh diperolehi dengan terbitan tersirat.

Contoh

Memandangkan elips berikut, cari "y":

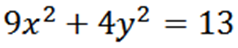
Secara tersirat memperoleh berkenaan dengan x, kita ada:

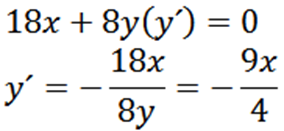
Kemudian, dapatkan semula secara tersirat berkenaan dengan x, memberi kita:

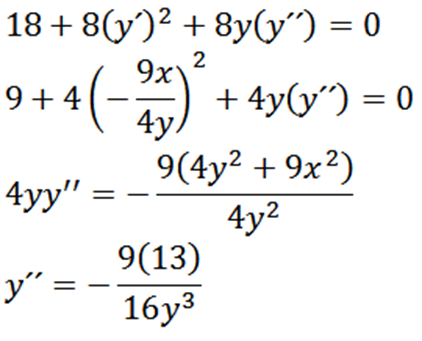
Akhirnya, kita ada:

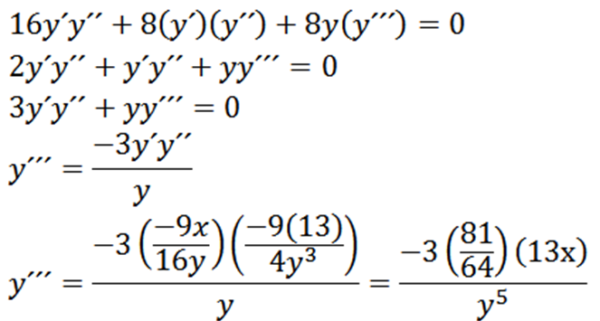
Ekstrem relatif

Penggunaan lain yang boleh kita berikan kepada derivatif kedua -order adalah dalam pengiraan hujung relatif fungsi.

Boleh melayani anda: Berapa banyak paksi simetri?

Kriteria derivatif pertama untuk ekstrem tempatan memberitahu kita bahawa jika kita mempunyai fungsi F yang berterusan dalam selang (a, b) dan ada c yang dimiliki oleh selang tersebut sehingga ia dibatalkan dalam c (iaitu, c adalah titik kritikal), salah satu daripada tiga kes ini boleh berlaku:

• Jika f '(x)> 0 untuk mana -mana x milik (a, c) dan f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Jika f '(x) 0 untuk x milik (c, b), maka f (c) adalah minimum tempatan.
• Jika f '(x) mempunyai tanda yang sama (a, c) dan dalam (c, b), ia menunjukkan bahawa f (c) bukan akhir tempatan.

Menggunakan kriteria derivatif kedua kita dapat mengetahui jika bilangan kritikal fungsi adalah maksimum atau minimum tempatan, tanpa perlu melakukan apakah tanda fungsi pada selang waktu yang disebutkan di atas.

Kriteria drift kedua memberitahu kita bahawa jika f '(c) = 0 dan f "(x) berterusan dalam (a, b), ia berlaku jika f" (c)> 0 maka f (c) adalah a Minimum tempatan dan jika f "(c) < 0 entonces f(c) es un máximo local.

Jika f "(c) = 0, kita tidak dapat menyimpulkan apa -apa.

Contoh

Memandangkan fungsi f (x) = x⁴ + (4/3) x³ - 4x², Cari relatif maksimum dan minimum f yang menggunakan kriteria derivatif kedua.

Mula -mula kita mengira f '(x) dan f "(x) dan kita ada:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Sekarang, f '(x) = 0 ya, dan hanya jika 4x (x + 2) (x - 1) = 0, dan ini berlaku apabila x = 0, x = 1 atau x = - 2.

Untuk menentukan sama ada nombor kritikal yang diperoleh adalah ekstrem relatif hanya menilai dalam f "dan dengan itu memerhatikan tandanya.

Boleh melayani anda: heptagon

f "(0) = - 8, jadi f (0) adalah maksimum tempatan.

f "(1) = 12, jadi f (1) adalah minimum tempatan.

f "(- 2) = 24, jadi f (- 2) adalah minimum tempatan.

Siri Taylor

Jadilah fungsi yang ditakrifkan seperti berikut:

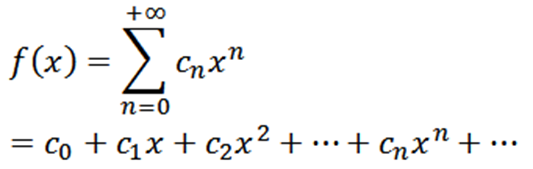
Fungsi ini mempunyai jejari konvergensi r> 0 dan telah diperoleh dari semua pesanan dalam (-r, r). Derivatif berturut -turut f memberi kita:

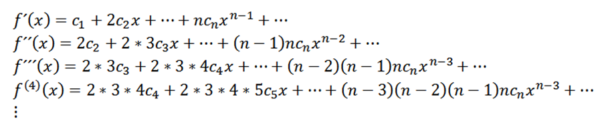
Mengambil x = 0, kita boleh mendapatkan nilai c_n Bergantung pada derivatifnya seperti berikut:

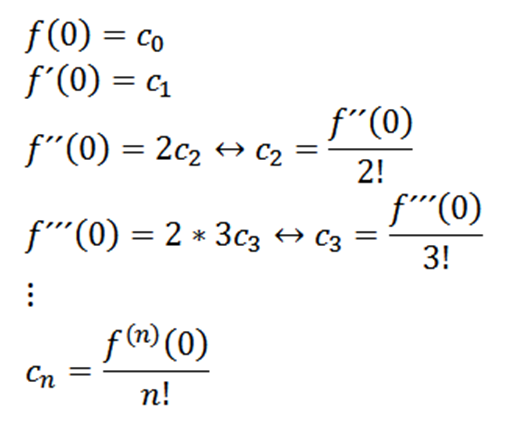
Jika kita mengambil n = 0 sebagai fungsi f (iaitu, f^0 = f), maka kita boleh menulis semula fungsi seperti berikut:

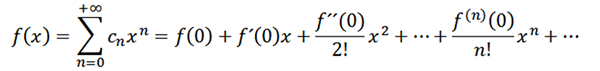
Sekarang mari kita pertimbangkan fungsi sebagai satu siri kuasa di x = a:

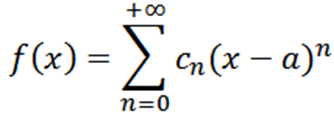
Jika kita melakukan analisis yang sama dengan yang sebelumnya, kita perlu menulis fungsi f sebagai:

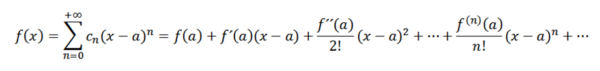
Siri ini dikenali sebagai Taylor F dalam siri. Apabila A = 0 kita mempunyai kes tertentu yang disebut siri MacLaurin. Siri jenis ini adalah kepentingan matematik yang hebat terutamanya dalam analisis berangka, kerana terima kasih kepada ini kita dapat menentukan fungsi dalam komputer seperti e^x , dosa (x) dan cos (x).

Contoh

Dapatkan siri MacLaurin untuk e^x.

Perhatikan bahawa jika f (x) = e^x, Kemudian f^(N)(x) = e^x dan f^(N)(0) = 1, jadi siri MacLaurin anda ialah: