Matematik

Ketidaksamaan segitiga demonstrasi, contoh, latihan diselesaikan

Ketidaksamaan segitiga demonstrasi, contoh, latihan diselesaikan

Ia dikenali sebagai Ketidaksamaan segitiga kepada harta yang memenuhi dua nombor sebenar yang terdiri daripada nilai mutlak jumlahnya adalah kurang daripada atau sama dengan jumlah nilai mutlaknya. Harta ini juga dikenali sebagai ketidaksamaan Minkowski atau ketidaksamaan segi tiga.

Harta benda ini dipanggil ketidaksamaan segi tiga kerana di segitiga ia berlaku bahawa panjang satu sisi sentiasa kurang daripada atau sama dengan jumlah dua yang lain, walaupun ketidaksamaan ini tidak selalu berlaku di dalam bidang segitiga.

Rajah 1. Nilai mutlak jumlah dua nombor selalu kurang dari atau sama dengan jumlah nilai mutlaknya. (Disediakan oleh r. Pérez)

Terdapat beberapa demonstrasi ketidaksamaan segi tiga dalam bilangan sebenar, tetapi dalam hal ini kita akan memilih A berdasarkan sifat nilai mutlak dan binomial persegi.

Teorem: Untuk semua nombor nombor ke dan b Kepunyaan nombor sebenar, ia harus:

| A + B | ≤ | a | + | B |

[TOC]

Demonstrasi

Kami mulakan dengan mempertimbangkan ahli pertama ketidaksamaan, yang akan ditebang:

| A + b |^2 = (a + b)^2 = a^2 + 2 a b + b^2 (ec. 1)

Dalam langkah sebelumnya, harta itu telah digunakan bahawa mana -mana nombor yang tinggi ke dataran adalah sama dengan nilai mutlak nombor tersebut tinggi ke dataran, iaitu: | x |^2 = x^2. Perkembangan binomial persegi juga telah digunakan.

Semua nombor x Ia kurang dari atau sama dengan nilai mutlaknya. Sekiranya bilangannya positif, ia bernilai kesamaan, tetapi jika bilangannya negatif, ia akan menjadi kurang daripada bilangan positif. Dalam kes ini nilai mutlaknya sendiri, iaitu boleh dinyatakan bahawa x ≤ | X |.

Boleh melayani anda: Pengaturcaraan bukan linear: Kaedah dan Latihan

Produk (A B) Ia adalah nombor, oleh itu ia digunakan (a b) ≤ | A B |. Apabila harta ini digunakan untuk (EC. 1) Kami ada:

| A + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | A B | + B^2 (EC. 2)

Dengan mengambil kira bahawa | A B | = | A || B | LA (EC. 2) Ia boleh ditulis seperti berikut:

 | A + b |^2 ≤ a^2 + 2 | A || B | + B^2 (EC. 3)

Tetapi seperti yang telah kita katakan sebelum ini bahawa kuadrat nombor adalah sama dengan nilai mutlak nombor yang tinggi ke dataran, maka Persamaan 3 dapat ditulis semula seperti berikut:

 | A + b |^2 ≤ | a |^2 + 2 | a | | B | + | B |^2 (EC. 4)

Dalam ahli kedua ketidaksamaan, produk yang luar biasa diiktiraf, yang apabila diterapkan membawa kepada:

 | A + b |^2 ≤ (| a | + | b |)^2 (EC. 5)

Dalam ungkapan sebelumnya, perlu diperhatikan bahawa nilai -nilai yang akan dibangkitkan pada kedua -dua anggota ketidaksamaan juga positif bahawa ia juga harus dipenuhi bahawa:

 | A + B | ≤ (| a |+ | b |) (EC. 6)

Ungkapan sebelumnya betul -betul apa yang anda mahu tunjukkan.

Contoh

Seterusnya kita akan memeriksa ketidaksamaan segi tiga dengan beberapa contoh.

Contoh 1

Nilai diambil A = 2 dan nilai b = 5, iaitu nombor positif dan kami mengesahkan sama ada atau tidak ketidaksamaan dipenuhi.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Kesamaan disahkan, oleh itu teorem ketidaksamaan segitiga telah dipenuhi.

Contoh 2

Nilai berikut dipilih a = 2 dan b = -5, iaitu nombor positif dan negatif yang lain, kita periksa sama ada atau tidak ketidaksamaan dipenuhi.

Boleh melayani anda: trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Ketidaksamaan dipenuhi, oleh itu teorem ketidaksamaan segi tiga telah disahkan.

Contoh 3

Nilai diambil A = -2 dan nilai B = 5, iaitu nombor negatif dan yang lain positif, kami mengesahkan sama ada atau tidak ketidaksamaan dipenuhi.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Ketidaksamaan disahkan, oleh itu teorem telah dipenuhi.

Contoh 4

Nilai berikut a = -2 dan b = -5 dipilih, iaitu, kedua -dua nombor negatif dan kita periksa sama ada atau tidak ketidaksamaan dipenuhi.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Kesaksamaan disahkan, oleh itu teorem ketidaksamaan Minkowsk telah dipenuhi.

Contoh 5

Nilai diambil a = 0 dan nilai b = 5, iaitu nombor sifar dan yang lain positif, maka kita periksa sama ada atau tidak ketidaksamaan dipenuhi.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Kesamaan dipenuhi, oleh itu teorem ketidaksamaan segitiga telah disahkan.

Contoh 6

Nilai diambil A = 0 dan nilai b = -7, iaitu nombor sifar dan yang lain positif, maka kita periksa sama ada atau tidak ketidaksamaan dipenuhi.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Kesamaan disahkan, oleh itu teorem ketidaksamaan segi tiga telah dipenuhi.

Latihan yang diselesaikan

Dalam latihan berikut secara geometri mewakili ketidaksamaan segitiga atau ketidaksamaan Minkowski untuk nombor A dan B.

Boleh melayani anda: papomudas

Nombor A akan diwakili sebagai segmen pada paksi x, asalnya atau bertepatan dengan sifar paksi x dan hujung segmen (pada titik p) akan berada di arah positif (ke kanan) x paksi jika> 0, tetapi ke < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Begitu juga, nombor b akan diwakili sebagai segmen yang asalnya pada titik p. Akhir yang lain, iaitu, titik yang akan berada di sebelah kanan p jika b adalah positif (b> 0) dan titik q akan | b | unit di sebelah kiri p jika b<0.

Latihan 1

Secara grafik mewakili ketidaksamaan segitiga untuk a = 5 dan b = 3 | A + B | ≤ | a | + | B |, menjadi C = a + b. 

Penyelesaian 1: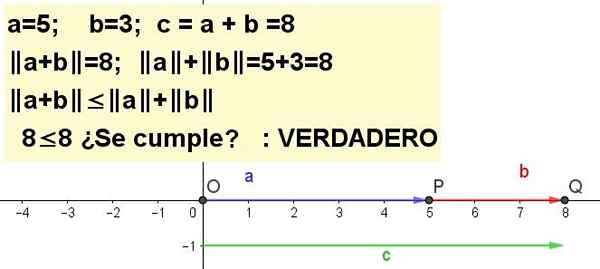

Latihan 2

Buat graf ketidaksamaan segi tiga untuk a = 5 dan b = -3. 

| A + B | ≤ | a | + | B |, menjadi C = a + b.

Penyelesaian 2:

Latihan 3

Graf ketidaksamaan segitiga untuk a = -5 dan b = 3.

| A + B | ≤ | a | + | B |, menjadi C = a + b. 

Penyelesaian 3: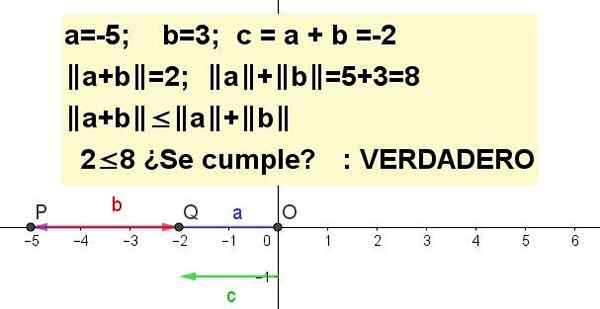

Latihan 4

Graf ketidaksamaan segi tiga untuk a = -5 dan b = -3.

| A + B | ≤ | a | + | B |, menjadi C = a + b.

Penyelesaian 4: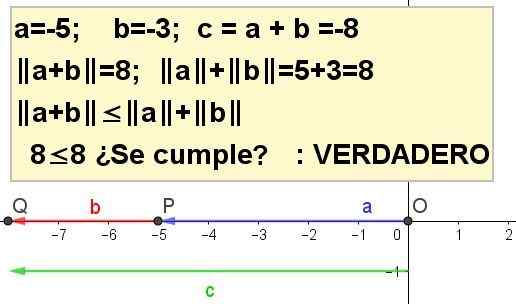

Rujukan

  1. Dan. Whitesitt. (1980).Algebra Boolean dan aplikasinya . Syarikat Editorial Continental C. Ke.
  2. Mícheal atau 'searcoid.(2003) Unsur Analisis Abstrak ... Jabatan Matematik. Universiti Kolej Dublin, Beldfield, Dublind.
  3. J. Van Wyk. (2006) Matematik dan Kejuruteraan dalam Sains Komputer. Institut Sains dan Teknologi Komputer. Biro Piawaian Kebangsaan. Washington, d. C. 20234
  4. Eric Lehman. Matematik untuk Sains Komputer.  Google Inc.
  5. F Thomson Leighton (1980). Kalkulus. Jabatan Matematik dan Sains Komputer dan Makmal AI, Institut Teknologi Massachussetts.
  6. Akademi Khan. Teorem Ketidakseimbangan Segitiga. Pulih dari: Khanacademy.org
  7. Wikipedia. Ketidaksamaan segi tiga. Pulih dari: Adakah. Wikipedia.com