Anjakan sudut

Apa itu anjakan sudut?

Dia Anjakan sudut Ini adalah perubahan atau variasi dalam kedudukan sudut yang objek dalam pengalaman putaran, biasanya diukur dalam radian atau langkah lain yang diberikan untuk giliran, seperti gred atau revolusi.

Apabila objek berkisar di sekitar paksi tetap, anjakan sudutnya ditentukan dengan mengukur sudut yang disapu oleh garis yang melewati mana -mana titik badan yang memotong paksi putaran, iaitu, garis radial.

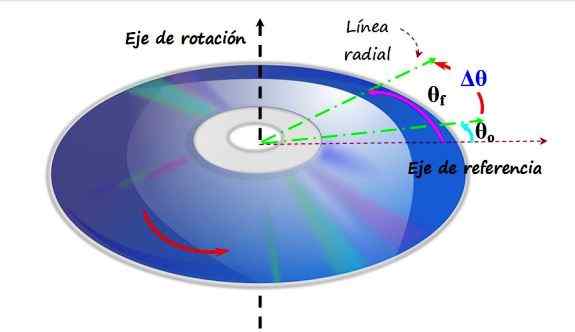Cakera padat atau CD berkisar dalam arah antihoranant di sekitar paksi putaran menegak. Semasa berlalu dari sudut θo ke θf, dikatakan bahawa ia telah mengalami anjakan sudut. Sumber: f. Zapata.

Di bahagian atas terdapat CD yang berputar dalam arah anti -horari, sebagai paksi putaran paksi menegak. Paksi rujukan diletakkan di atas satah CD, yang sepadan dengan sudut 0 radian atau 0. Garis hijau adalah garis radial, yang pada mulanya membentuk sudut θ_{Sama ada} Dengan rujukan. Ini adalah kedudukan awal anda.

Kemudian garis hijau bergerak ke kedudukan baru yang disebut θ_F, Dan pengalaman yang dialami, yang dipanggil Δθ adalah semata -mata:

Δθ = θ_F - θ_{Sama ada}

Mana -mana titik P CD mengalami anjakan sudut yang sama dalam selang masa tertentu, kecuali pusat, di mana paksi putaran berlalu dan kekal berehat.

Formula dan persamaan

Terdapat objek yang berkisar di sekitar paksi tetap atau yang meninggalkan skrin ke pembaca. Dan di dalamnya, terdapat titik p, terletak pada jarak r paksi putaran dan menggambarkan lingkaran radio r.

Ini dilihat dalam angka berikut, yang menunjukkan objek pemotongan, dilihat bertentangan dengan jarum jam. Titik yang dipersoalkan adalah dalam kedudukan sudut θ, diukur dari paksi rujukan, yang dalam hal ini adalah paksi mendatar.

Boleh melayani anda: prinsip aditif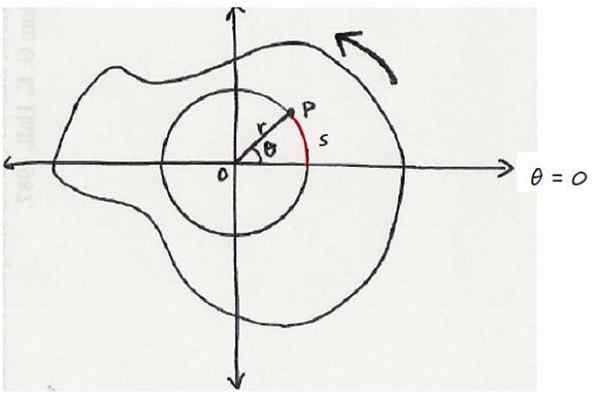Objek yang berputar dalam erti kata anti -horari. Paksi putaran keluar tegak lurus ke skrin. Sumber: Wikimedia Commons.

Oleh konvensyen, kepada putaran dalam pengertian antihorarial, ia diberikan rasa positif, sementara putaran dalam jadual mempunyai tanda negatif.

Sebagai titik p bersumpah sudut θ, secara serentak mengembara arka. Oleh kerana θ adalah sudut pusat, kerana puncaknya menduduki pusat lilitan, ia dipenuhi bahawa:

Dengan θ dinyatakan dalam radianes.

Anjakan sudut adalah:

Δθ = θ_final  - θ_permulaan

Contohnya, jika p bermula dengan θ_permulaan = 0 rad dan kemudian berada di θ_final = 0.8 rad, anjakan sudutnya adalah dari:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Titik lain objek boleh menduduki kedudukan sudut yang berbeza, tetapi semua mengalami anjakan sudut yang sama. Walau bagaimanapun, zarah -zarah yang paling jauh dari pusat perjalanan jauh lebih jauh, kerana s = r ⋅θ.

Ukuran sudut

Dalam putaran adalah perkara biasa untuk mencari sudut yang diukur dalam radian, tetapi mereka juga didapati dalam darjah dan revolusi atau bertukar. Dalam penyelesaian masalah, perlu bergerak dari unit -unit ini ke radian.

1 Revolusi bersamaan dengan giliran lengkap, iaitu, apabila giliran lengkap pecah, ia telah bertukar 360 º dan ini bersamaan dengan 2 π radians, kerana dalam kes itu, titik melawat arka sama dengan 2πr:

Tetapi mempermudahkan, kesetaraan sebelumnya boleh dinyatakan seperti berikut:

π Radianes = 180º

Bagaimana anjakan sudut dikira?

Anjakan sudut dapat dikira secara analog dengan bagaimana anjakan dalam pergerakan dikira dalam dimensi, berikutan model pergerakan tertentu. Untuk ini, halaju sudut purata ditakrifkan sebagai anjakan sudut Δθ dalam selang waktu tertentu Δt:

Di mana halaju sudut purata dilambangkan sebagai Ω_m dan diberikan dalam radian/s dalam unit sistem antarabangsa jika.

Boleh melayani anda: bagaimana untuk mendapatkan sudut segitiga? (Contoh)

Halaju sudut segera adalah had halaju sudut purata apabila Δt → 0:

Iaitu, ia adalah yang pertama berasal dari kedudukan sudut berkenaan dengan masa. Sebaliknya, pecutan sudut boleh ditakrifkan, dilambangkan sebagai α, yang bersamaan dengan kadar derivatif atau perubahan halaju sudut berkenaan dengan masa:

Yang juga boleh ditafsirkan sebagai yang kedua yang diperoleh dari kedudukan sudut berkenaan dengan masa.

Yang penting ialah dua model pergerakan dapat ditubuhkan dalam analogi dengan pergerakan rectilinear, kerana walaupun putaran dilakukan dalam satah, satu koordinat sudut tunggal cukup untuk menetapkan kedudukan mana -mana titik objek.

Gerakan bulat seragam

Dalam pergerakan pekeliling seragam, halaju sudut tetap, iaitu, halaju sudut purata sama dengan halaju sudut segera. Sebagai pecutan sudut α adalah sama dengan 0, anda boleh menulis persamaan berikut untuk kedudukan sebagai fungsi masa:

θ = θ_{Sama ada} + ωt

Di mana θ_{Sama ada} Ia adalah kedudukan awal mudah alih.

Pergerakan pekeliling yang dipercepatkan secara seragam

Dalam kes ini, pecutan sudut α adalah malar, dan dalam analogi dengan pergerakan rectilinear yang bervariasi seragam, persamaan berikut boleh ditulis:

• θ = θ_{Sama ada} + Ω_{Sama ada} T + ½ αt²
• Ω = Ω_{Sama ada} + αt 
• Ω² = Ω_{Sama ada}² + 2α ∙ Δθ

Latihan diselesaikan

Latihan pertama

Dapat diandaikan bahawa bumi adalah objek tegar yang berkisar pada paksi tetap dan putarannya hampir seragam. Dalam selang waktu Δt = 12 h cari:

a) anjakan sudut bumi

b) halaju sudut anda

c) pecutan sudut semasa selang waktu itu.

Penyelesaian kepada

Mengetahui bahawa dalam masa 24 jam bumi mengambil giliran lengkap paksi, dalam 12 jam anda akan bertukar separuh daripada pusingan, iaitu, π radianes. Sekiranya dianggap bahawa bahagian θ_permulaan = 0 rad, maka anjakan sudutnya ialah:

Boleh melayani anda: Prinsip Multiplicative: Mengira Teknik dan Contoh

Δθ = π radians

Penyelesaian b

Sebagai putaran adalah seragam, halaju sudut adalah kuota antara anjakan sudut dan masa, sebagai tambahan, 1 jam = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Penyelesaian c

Pecutan sudut tidak sah, kerana putaran bumi adalah seragam.

Latihan kedua

Juan telah menjalankan jarak 35 meter pada trek olahraga bulat yang radius sama dengan 7 meter. Kirakan anjakan sudut yang dibuat Juan.

Penyelesaian

Oleh kerana jarak gerbang yang dilalui dan jejari lilitan diketahui, formula kedua boleh digunakan untuk mengetahui anjakan sudut yang dibuat oleh Juan. Menggunakan formula yang diterangkan di atas anda perlu θ = 35/7 = 5 radian.

Latihan ketiga

Sekiranya Mario terpaksa berada di dalam kenderaannya, separuh daripada trek perlumbaan bulat, apakah anjakan sudut yang dilakukan Mario?

Penyelesaian

Dalam latihan ini formula pertama akan dikenakan. Oleh kerana diketahui bahawa Mario telah mengembara separuh dari trek, dapat diandaikan bahawa dia memulakan perlumbaan di Angle 0 ° dan ketika ia mencapai separuh dari lilitan yang dia telah mengembara 180 °. Oleh itu, jawapannya ialah 180 ° -0 ° = 180 ° = π radians.

Latihan keempat

Maria mempunyai kolam bulat. Anjing anda berjalan di sekitar kolam renang yang bergerak sejauh 18 meter. Sekiranya jejari kolam renang adalah 3 meter, apakah anjakan sudut yang dibuat oleh haiwan kesayangan Maria?

Penyelesaian

Oleh kerana kolam adalah bulat dan jejari itu diketahui, anda boleh meneruskan menggunakan formula kedua.

Diketahui bahawa jejari adalah sama dengan 3 meter, dan jarak yang dilalui oleh haiwan kesayangan adalah sama dengan 18 meter. Oleh itu, anjakan sudut yang dilakukan adalah sama dengan θ = 18/3 = 6 radian.

Rujukan

1. Katz, d. 2013. Fizik untuk saintis dan jurutera. Asas dan sambungan. Pembelajaran Cengage.
2. Rex, a. 2011. Asas Fizik. Pearson.
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.
5. Tipler, ms. (2006). Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 1. Editorial kembali.