Persamaan umum garis yang cerunnya sama dengan 2/3

Persamaan umum garis L adalah seperti berikut: kapak+oleh+c = 0, di mana a, b dan c adalah malar, x adalah pembolehubah bebas e dan pemboleh ubah bergantung.

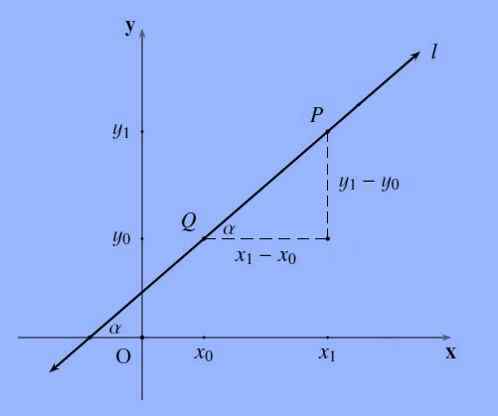
Cerun garis, dilambangkan dengan cara umum dengan huruf m, yang melewati titik p = (x1, y1) dan q = (x0, y0) adalah quotient berikut m: = (y1-y0)/(x1 -X0).

Cerun garis lurus mewakili kecenderungan; Kata lebih formal, cerun garis adalah tangen sudut yang bentuk ini dengan paksi x.

Harus diingat bahawa urutan di mana titik-titik yang dinamakan adalah acuh tak acuh, kerana (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Garis yang belum selesai

Sekiranya dua mata diketahui di mana garis berlalu, mudah untuk mengira cerunnya. Tetapi apa yang berlaku jika perkara ini tidak diketahui?

Memandangkan persamaan umum kapak+oleh+c = 0 baris, ia harus.

Apakah persamaan umum garis yang cerunnya 2/3?

Oleh kerana cerun garisan adalah 2/3 maka kesamaan ditubuhkan -a/b = 2/3, yang dapat melihat bahawa a = -2 dan b = 3. Supaya persamaan umum garis dengan cerun sama dengan 2/3 ialah -2x+3y+c = 0.

Harus dijelaskan bahawa jika anda dipilih A = 2 dan B = -3, persamaan yang sama akan diperolehi. Sesungguhnya, 2x -3y+c = 0, yang sama dengan yang terdahulu didarab dengan -1. Tanda C tidak penting, kerana ia adalah pemalar umum.

Satu lagi pemerhatian yang boleh dibuat ialah untuk A = -4 dan B = 6 baris yang sama diperoleh, walaupun persamaan umumnya berbeza. Dalam kes ini persamaan umum ialah -4x+6y+c = 0.

Adakah terdapat cara lain untuk mencari persamaan umum garis?

Jawapannya ya. Sekiranya cerun garis diketahui terdapat dua bentuk, tambahan kepada yang sebelumnya, untuk mencari persamaan umum.

Untuk ini, persamaan titik-penangguhan dan persamaan pemotongan digunakan.

-Persamaan Titik-Mendapatkan: Jika M adalah cerun garis dan p = (x0, y0) titik di mana ia berlalu, maka persamaan y-y0 = m (x-x0) dipanggil persamaan titik-penampalan.

-Persamaan pemotongan: Jika m adalah cerun garis dan (0, b) adalah pemotongan garis dengan paksi y, maka persamaan y = mx+b dipanggil persamaan pemotongan-pending.

Menggunakan kes pertama, diperolehi bahawa persamaan titik-titik garis yang cerunnya 2/3 diberikan oleh ungkapan Y-Y0 = (2/3) (X-X0).

Untuk mencapai persamaan umum, semua istilah didarabkan oleh 3 di kedua -dua belah pihak dan dikelompokkan bersama, dengan itu memperoleh -2x+3y+(2 × 0-3y0) = 0 adalah persamaan umum garis, di mana c = 2 × 0-3Y0.

Sekiranya kes kedua digunakan, diperolehi bahawa persamaan pemotongan garis-garis yang cerunnya 2/3 adalah y = (2/3) x+b.

Sekali lagi, mendarabkan 3 di kedua -dua belah pihak, dan mengumpulkan semua pembolehubah, ia diperoleh -2x+3y -3b = 0. Yang terakhir adalah persamaan umum garis di mana c = -3b.

Sebenarnya, melihat dengan teliti pada kedua -dua kes, dapat dilihat bahawa kes kedua hanyalah kes tertentu yang pertama (ketika x0 = 0).