Formula Persamaan Gred Pertama, Cara Menyelesaikannya, Contoh, Latihan

The Persamaan tahap pertama atau linear Dengan yang tidak diketahui adalah mereka yang boleh dinyatakan sebagai jumlah dua istilah, dengan cara berikut:

kapak + b = 0

Di mana a dan b, dengan ke ≠ 0, adalah nombor sebenar r atau juga kompleks c. Untuk menyelesaikannya, istilah dipindahkan, yang bermaksud mengubah istilah dari satu sisi ke persamaan yang lain.

Rajah 1. Persamaan linear ialah borang y = mx + c dengan y = 0. Sumber: Pxhere.

Untuk membersihkan yang tidak diketahui, istilah +b ditransposikan, yang mesti pergi ke sebelah kanan persamaan dengan tanda yang berubah.

Ax = -b

Kemudian nilai x dibersihkan, dengan cara ini:

x = - b/a

Sebagai contoh kita akan menyelesaikan persamaan berikut:

6x - 5 = 4

Kami menukar istilah -5 ke sebelah kanan dengan tanda yang berubah:

6x = 4 + 5

Ini bersamaan dengan menambah 5 di kedua -dua belah persamaan asal:

6x - 5 + 5 = 4 + 5 → 6x = 9

Dan sekarang kita membersihkan "x" yang tidak diketahui:

x = 9/6 = 3/2

Yang bersamaan dengan membahagikan kedua -dua belah persamaan dengan 6. Oleh itu, kita dapat menilai yang berikut untuk mendapatkan penyelesaian:

-Jumlah yang sama boleh ditambah atau dikurangkan kedua -dua belah persamaan dalam persamaan, tanpa mengubahnya.

-Anda juga boleh membiak (atau membahagikan) dengan jumlah yang sama dengan semua istilah di sebelah kiri dan di sebelah kanan persamaan.

-Dan jika kedua -dua anggota persamaan meningkat kepada kuasa yang sama, kesamaan tidak diubah sama ada.

[TOC]

Cara menyelesaikan persamaan ijazah pertama

Penyelesaian persamaan ijazah pertama juga dikenali sebagai akar yang sama. Ia adalah nilai x yang menukarkan ungkapan asal menjadi kesamaan. Contohnya dalam:

5x = 8x - 15

Jika kita menggantikan x = 5 dalam persamaan ini, ia diperolehi:

5 ⋅5 = 8 ⋅5 - 15

25 = 40 - 15

25 = 25

Sebagai persamaan linear darjah pertama datang dalam pelbagai cara, yang kadang -kadang tidak jelas, terdapat satu siri peraturan umum yang terdiri daripada beberapa manipulasi algebra, untuk mencari nilai yang tidak diketahui:

-Pertama, jika ada operasi yang ditunjukkan, ini mesti dijalankan.

-Simbol pengelompokan seperti tanda kurung, kurungan dan kunci persegi, jika ada, mesti ditindas dengan mengekalkan tanda -tanda yang sesuai.

-Syarat -syarat yang ditransmisikan untuk menempatkan semua yang mengandungi yang tidak diketahui dengan satu sisi persamaan, dan yang tidak mengandunginya.

-Maka semua istilah yang serupa dikurangkan, untuk mencapai borang Ax = -b.

-Dan langkah terakhir adalah untuk membersihkan yang tidak diketahui.

Tafsiran grafik

Persamaan ijazah pertama yang dibangkitkan pada mulanya dapat diperoleh dari persamaan garis y = mx+c, melakukan y = 0. Nilai x yang hasilnya sepadan dengan persimpangan garis dengan paksi mendatar.

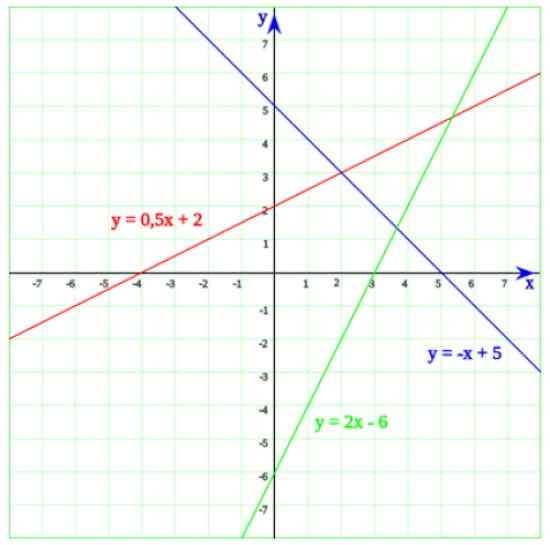
Dalam angka berikut, anda mempunyai tiga baris. Bermula dengan garis hijau, yang persamaannya adalah:

Boleh melayani anda: pemfaktoran

y = 2x - 6

Membuat Y = 0 dalam baris garis persamaan ijazah pertama diperolehi:

2x - 6 = 0

Penyelesaiannya ialah x = 6/2 = 3. Sekarang apabila kita memperincikan graf, mudah untuk menyedari bahawa pada dasarnya, garis memotong ke paksi mendatar pada x = 3.

Garis biru memotong paksi x pada x = 5, yang merupakan penyelesaian kepada persamaan -x + 5 = 0. Akhirnya, garis yang persamaannya adalah y = 0.5x + 2 dipotong ke paksi x pada x = -4, yang mudah diberi amaran persamaan ijazah pertama:

0.5 x + 2 = 0

x = 2/0.5 = 4

Rajah 2. Tiga baris yang persimpangannya dengan paksi mendatar sesuai dengan persamaan linear. Sumber: Wikimedia Commons.

Contoh persamaan linear sederhana   

Keseluruhan persamaan

Mereka adalah orang -orang yang istilahnya tidak ada penyebut, sebagai contoh:

21 - 6x = 27 - 8x

Penyelesaiannya ialah:

-6x + 8x = 27 - 21

2x = 6

x = 3

Persamaan pecahan

Persamaan ini mengandungi sekurang -kurangnya satu penyebut yang berbeza dari 1. Untuk menyelesaikannya, adalah dinasihatkan.

Persamaan berikut adalah jenis pecahan:

Penyebutnya adalah 6, 8 dan 12 dan pelbagai minimum mereka, dilambangkan sebagai m.c.M (6, 8,12) adalah sedikit pun dari angka -angka yang mengandungi penyebut ini.

Oleh kerana nombor ini kecil, tidak sukar untuk melihat bahawa m.c.M (6, 8,12) = 24. Hasil ini mudah diperoleh dengan menyatakan nombor sebagai produk nombor utama atau kuasa mereka, mari kita lihat:

6 = 3.2

8 = 2³

12 = 2²⋅3

Pelbagai biasa minimum ditentukan dengan mendarabkan faktor biasa dan bukan umum sebanyak 6, 8 dan 12 dengan eksponen terbesarnya, kemudian:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Oleh kerana pelbagai biasa minimum tersedia, ia mesti didarabkan dengan setiap syarat persamaan:

Dengan cara ini, penyebut ditindas dan terdapat persamaan dengan produk, lebih mudah untuk diselesaikan:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Kami menggunakan harta pengedaran:

4x + 20 - 6x -9 = 2 - 10x

Semua istilah yang mengandungi "x" yang tidak diketahui dikelompokkan ke sebelah kiri persamaan, meninggalkan istilah bebas atau berangka sebelah kanan:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Persamaan literal

Mereka adalah persamaan linear dengan yang tidak diketahui, yang bagaimanapun disertai dengan pekali literal (huruf). Surat -surat ini dirawat seperti yang akan dilakukan dengan nombor. Contoh persamaan pertama yang literal adalah:

-3ax + 2a = 5x - b

Persamaan ini diselesaikan dengan cara yang sama seolah -olah terma dan pekali bebas adalah berangka:

-3ax - 5x = - b - 2a

Memfokuskan "x" yang tidak diketahui:

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Sistem Persamaan Ijazah Pertama 

Sistem persamaan terdiri daripada satu set persamaan dengan dua atau lebih yang tidak diketahui. Penyelesaian sistem terdiri daripada nilai -nilai yang memenuhi persamaan secara serentak dan untuk menentukannya secara tegas, mesti ada persamaan untuk setiap yang tidak diketahui.

Boleh melayani anda: aljabar vektor

Bentuk umum sistem m Persamaan linear dengan n tidak diketahui adalah:

ke_sebelasx₁ + ke₁₂x₂ +... ke_1nx_n = b₁
ke_{dua puluh satu}x₁ + ke₂₂x₂ +... ke_2nx_n = b₂
…
ke_M1x₁ + ke_m2x₂ +... ke_mnx_n = b_m

Sekiranya sistem mempunyai penyelesaian, dikatakan bahawa ia adalah serasi yang ditentukan, Apabila terdapat set nilai tak terhingga yang memuaskannya tidak sesuai, Dan akhirnya, jika ia tidak mempunyai penyelesaian, maka itu adalah tidak serasi.

Dalam resolusi sistem persamaan linear beberapa kaedah digunakan: pengurangan, penggantian, penyamaan, kaedah grafik, penghapusan Gauss-Jordan dan penggunaan penentu adalah antara yang paling banyak digunakan. Tetapi ada algoritma lain untuk mencapai penyelesaian, lebih mudah untuk sistem dengan banyak persamaan dan tidak diketahui.

Contoh sistem persamaan linear dengan dua orang yang tidak diketahui ialah:

8x - 5 = 7y - 9
6x = 3y + 6

Penyelesaian sistem ini dikemukakan kemudian di bahagian Latihan yang diselesaikan.

Persamaan linear dengan nilai mutlak

Nilai mutlak nombor sebenar adalah jarak antara lokasinya pada baris nombor dan 0 yang sama. Menjadi jarak nilainya selalu positif.

Nilai mutlak nombor dilambangkan oleh bar modul: │x│. Nilai mutlak nombor positif atau negatif sentiasa positif, sebagai contoh:

│+8 │ = 8

│-3│ = 3

Dalam persamaan dengan nilai mutlak, yang tidak diketahui adalah antara bar modul. Pertimbangkan persamaan mudah berikut:

│x│ = 10

Terdapat dua kemungkinan, yang pertama ialah x adalah nombor positif, dalam hal ini kita ada:

x = 10

Dan kemungkinan lain ialah x adalah nombor negatif, dalam kes ini:

x = -10

Ini adalah penyelesaian persamaan ini. Sekarang mari kita lihat contoh yang berbeza:

│x+6 │ = 11

Jumlah dalam bar boleh positif, maka:

x+6 = 11

x = 11 -6 = 5

Atau boleh menjadi negatif. Kalau macam itu:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

Dan nilai yang tidak diketahui adalah:

x = -17

Oleh itu, persamaan nilai mutlak ini mempunyai dua penyelesaian: x₁ = 5 dan x₂ = -17. Kami dapat mengesahkan bahawa kedua -dua penyelesaian membawa kepada kesamaan dalam persamaan asal:

│5+6 │ = 11

│11│ = 11

Dan

│-17+6 │ = 11

│-11 │ = 11

Latihan mudah diselesaikan

- Latihan 1

Selesaikan sistem persamaan linear berikut dengan dua orang yang tidak diketahui:

8x - 5 = 7y -9
6x = 3y + 6

Penyelesaian

Oleh kerana sistem ini dinaikkan, ia sesuai untuk menggunakan kaedah penggantian, kerana dalam persamaan kedua yang tidak diketahui x Ia hampir siap untuk pelepasan:

x = (3y + 6)/6

Boleh melayani anda: algebra

Dan anda boleh segera menggantikan persamaan pertama, yang kemudiannya menjadi persamaan pertama yang tidak diketahui dengan "Y":

8 [(3y + 6)/6] - 5 = 7y - 9

Penyebut boleh ditindas jika setiap istilah didarab dengan 6:

6 . 8 ⋅ [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9

8 ⋅ (3y + 6) - 30 = 42y - 54

Memohon harta pengedaran dalam jangka masa pertama ke kanan kesamaan:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Persamaan dapat dipermudahkan, kerana semua pekali adalah gandaan 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Dengan hasil ini kita pergi ke pelepasan x:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Latihan 2

Selesaikan persamaan berikut:

Penyelesaian

Dalam persamaan ini, produk muncul, dan mengikuti arahan yang diberikan pada mulanya, mereka mesti dibangunkan terlebih dahulu:

3x - 10x +14 = 5x + 36x + 12

Kemudian semua istilah yang mengandungi yang tidak diketahui dibawa ke sebelah kiri kesamaan, dan di sebelah kanan istilah bebas akan:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Latihan 3

Dengan menambahkan tiga sudut dalaman segitiga, 180º diperolehi. Yang terbesar melebihi kanak -kanak pada 35º, dan ini seterusnya melebihi 20º perbezaan antara yang terbesar dan sederhana. Apa sudutnya?

Penyelesaian

Kami akan memanggil "x" ke sudut utama, "y" ke medium dan "z" kepada anak. Apabila pernyataan menyatakan bahawa jumlahnya adalah 180º anda boleh menulis:

x + y + z = 180

Kemudian kita tahu bahawa yang tertua melebihi kanak -kanak dalam 35º, kita boleh menulis ini:

X = z + 35

Akhirnya, kanak -kanak melebihi 20 º kepada perbezaan antara yang terbesar dan sederhana:

Z = x - y + 20

Kami mempunyai sistem 3 persamaan dan 3 tidak diketahui:

x + y + z = 180

X = z + 35

Z = x - y + 20

Dengan membersihkan persamaan pertama, anda mempunyai:

Z = 180 - x - y

Memadankan yang ketiga:

180 - x - y = x - y + 20

Melewati yang tidak diketahui ke sebelah kiri seperti biasa:

-x - y - x + y = 20 - 180

"Y" dibatalkan dan kekal:

-2x = - 160

x = 80º

Persamaan kedua ialah nilai z:

Z = x - 35 = 80 - 35 = 45º

Dan nilai dan yang pertama atau ketiga:

y = 180 - x - z = 180 - 80 - 45 = 55º

Rujukan

1. Baldor. 1977. Algebra Elementary. Edisi Kebudayaan Venezuela.
2. Institut Monterey. Persamaan, ketidaksamaan dan nilai mutlak. Pulih dari: Montereyinstitute.org.
3. Guru dalam talian. Klasifikasi persamaan linear atau pertama. Pulih dari: Profesor sebaris.Cl.
4. Hoffman, J. Pemilihan masalah matematik. Jilid 2.
5. Jiménez, r. 2008. Algebra. Prentice Hall.
6. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.