Dalam situasi apakah fungsi linear dan kuadrat?

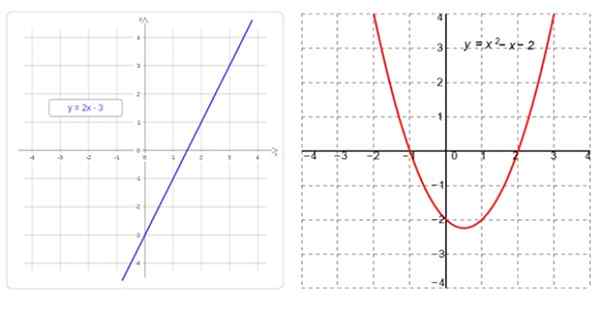
Di sebelah kiri fungsi linear, grafnya adalah garis lurus, dan di sebelah kanan, fungsi kuadratik, yang grafnya adalah parabola. Sumber: f. Zapata

Apakah fungsi linear dan kuadrat?

Fungsi linear dan fungsi kuadratik adalah fungsi yang tergolong dalam kumpulan fungsi polinom. Mereka digunakan untuk memodelkan pelbagai situasi, seperti pergantungan antara jumlah dan berat badan, kuantiti dan kos produk, kedudukan berbanding masa dan banyak lagi.

Secara umum, fungsi adalah hubungan yang menghubungkan dua pembolehubah dan boleh digunakan untuk memodelkan dunia nyata. Fungsi polinom, seperti namanya, dinyatakan melalui polinomial, yang bentuk umumnya adalah:

f (x) = a_nxⁿ + ke _N-1x ^N-1 + ke_X-2x^N-2 +... ke_{Sama ada}

Di mana n adalah nombor semula jadi, nombor untuk₀, ke₁, ke₂,... ke_n Mereka nyata, ke₀ Itu adalah istilah bebas dan ke_n, Ia adalah pekali yang mengiringi kuasa tertinggi. Nilai n menunjukkan jenis fungsi, untuk n = 1 fungsi linear, manakala untuk n = 2 fungsi adalah kuadrat.

Dalam kes yang pertama, ungkapan umum dikurangkan kepada:

f (x) = a₁x + a_{Sama ada}

Dan dalam kes kedua, ia tetap seperti ini:

f (x) = a₂x² + ke₁x + a_{Sama ada} ;   (Kepada₂≠ 0)

Grafik fungsi polinomial berterusan, ia. Oleh itu, mereka diperhatikan dalam pemodelan banyak situasi sains, ekonomi dan bidang pengetahuan manusia yang lain.

Seterusnya, aplikasi menarik antara satu sama lain diterangkan dengan lebih terperinci.

Situasi di mana fungsi linear muncul

Fungsi linear diwakili secara algebra oleh:

f (x) = a₁x + a_{Sama ada}

Atau setara:

f (x) = mx + b

Ciri tersendiri ialah grafnya adalah garis lurus. Nilai m, yang merupakan pekali x, mewakili Subang garis ini dan memberikan ukuran betapa cenderungnya.

Boleh melayani anda: Pengaturcaraan bukan linear: Kaedah dan Latihan

Lereng boleh menjadi positif, negatif atau sifar, tetapi ia sentiasa malar, iaitu kadar pertukarannya tetap tidak berubah.

Barisan cerun 0 adalah benar -benar mendatar, ia kenaikan, yang lain berkurangan).

Nilai b, Bagi bahagiannya, ia mewakili potongan atau persimpangan garis dengan paksi menegak. Yeah B = 0, Garis ini melalui asal -usul sistem koordinat.

Contoh pemodelan dengan fungsi linear

1. Pergerakan rectilinear seragam

Persamaan yang menghubungkan kedudukan x dan masa t mudah alih, dalam pergerakan rectilinear seragam, adalah linear:

x (t) = v ⋅T + x_{Sama ada}

Di mana V, cerun garis, adalah kelajuan mudah alih, yang tetap berterusan sepanjang pergerakan keseluruhan, dan x_{Sama ada} adalah kedudukan awal.

2. Ketumpatan

Ketumpatan objek atau bahan, yang mewujudkan hubungan antara jisim dan kelantangan. Memanggil ρ ke ketumpatan (ia berbunyi "rho"), m ke doh dan v ke kelantangan, anda mempunyai:

Membersihkan doh, dari segi jumlah, ia diperolehi:

M = ρv

Apabila grafik doh bergantung pada kelantangan, garis lurus diperolehnya yang cerun adalah ketumpatan objek atau bahan.

3. Panjang lilitan

Kontur bulatan, atau panjangnya, berkadar dengan jejarinya. Ini bermakna bahawa semakin besar jejari, semakin besar kontur lilitan, menurut persamaan:

Boleh melayani anda: pekali korelasi: formula, pengiraan, tafsiran, contoh

C = 2πr

Di mana c ialah kontur atau panjang, r ialah radio dan π (berbunyi "pi") adalah pemalar yang nilai anggarannya ialah πamp3.14 ..

4. Kos menghantar pakej

Seperti yang mudah disimpulkan, yang lebih berat atau besar adalah pakej yang lebih mahal adalah untuk mengangkutnya. Syarikat -syarikat yang didedikasikan untuk memodelkan harga kargo harga mereka mengikut peraturan tertentu, sebagai contoh:

C (x) = 2.75x

Dalam persamaan ini, c (x) adalah kos dolar untuk menghantar pakej yang beratnya x pound. Nilai malar 2.75 mempunyai unit dolar/paun (kos unit).

Situasi di mana fungsi kuadratik muncul

Secara algebra, fungsi kuadratik diwakili oleh:

f (x) = a₂ x² + ke₁ x + a_{Sama ada}

Dengan syarat pekali untuk₂ Berbeza dengan 0. Ia dicirikan oleh graf berbentuk parabola, yang paksi paksi atau paksi simetri adalah menegak (selari dengan paksi y)).

Persimpangan antara perumpamaan dan paksi berkata adalah titik yang dipanggil puncak. Sekiranya perumpamaan terbuka (a₂ > 0), puncak adalah titik minimumnya, dan jika ia dibuka (a₂ < 0), es el máximo.

Pada paksi simetri adalah tumpuan, titik khas yang menentukan kelengkungan parabola. Sekiranya cahaya matahari dipengaruhi pada cermin parabola, sinar akan dicerminkan di permukaan, bertepatan dengan fokus, yang dipanaskan dengan segera.

Contoh pemodelan dengan fungsi kuadrat

1. Ketinggian peluru yang dilancarkan secara menegak

Sebuah peluru adalah sebarang objek yang mana kelajuan awal disediakan dan kemudian dibebaskan, di bawah tindakan graviti. Jika kelajuan awal adalah menegak, magnitud v₀ dan diarahkan, objek akan naik ke ketinggian maksimum dan kemudian turun.

Boleh melayani anda: homotecia

Persamaan ketinggian h sebagai fungsi masa t ialah:

H (t) = -4.9 t²+v₀ t

Di mana rasa menegak diambil sebagai positif, dan menegak ke bawah negatif.

2. Trajektori peluru mendatar atau serong

Sekiranya kelajuan awal mendatar atau serong disediakan untuk peluru, ia akan menggambarkan trajektori parabola, yang boleh diwakili melalui fungsi kuadratik seperti yang digambarkan sebelumnya.

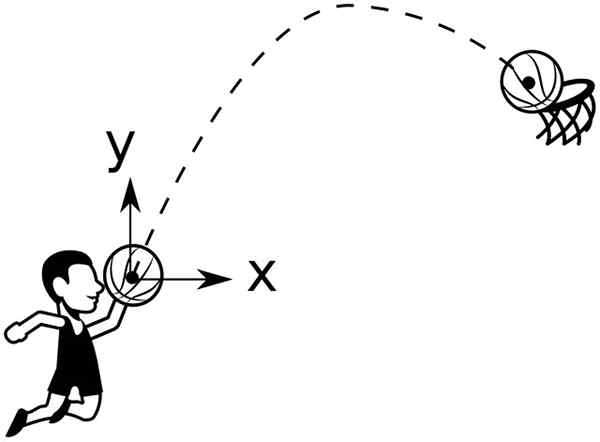Bola Keranjang menerangkan trajektori parabola untuk dibuang ke dalam bakul. Sumber: Wikimedia Commons

Contohnya, bola dilemparkan dari ketinggian dan₀, membentuk sudut θ₀ Mengenai mendatar, ia mempunyai trajektori yang diberikan oleh:

Dengan g sebagai pecutan graviti, yang boleh kira -kira 10 m/s². Contohnya, sepak bola sepak dari tanah (dan₀ = 0), dengan kelajuan awal 6 m/s dan sudut 45º berkenaan dengan mendatar, akan mempunyai trajektori yang diberikan oleh perumpamaan berikut:

3. Kawasan bulatan

Semakin tinggi jejari bulatan, semakin besar kawasannya. Sesungguhnya, kawasan bulatan adalah berkadar dengan kuadrat radius r, pemalar berkadar menjadi nombor π:

A = πr²

4. Keberkesanan iklan

Semakin mereka melihatnya, iklan komersial yang lebih berkesan. Keberkesanan E, pada skala dari 0 hingga 10, dari satu notis boleh dimodelkan mengikut fungsi kuadrat berikut:

Rujukan 

1. Fungsi polinom. Pulih dari sumber.pendidikan.adalah.
2. Larson, r. (2012). Precalculation. Ke -8. edisi. Pembelajaran Cengage.
3. Miller, c. (2013). Matematik: Penalaran dan Aplikasi. Ke -12. edisi. Pendidikan Pearson.
4. Stewart, J. (2012). Precalculation. Matematik untuk pengiraan. 6th. edisi. Pembelajaran Cengage.
5. Zill, d. (2008). Preccculment dengan kemajuan pengiraan. Ke -4. edisi. McGraw Hill.