Ruang vektor asas dan dimensi, aksioma, sifat

A ruang vektor Ia adalah set yang tidak berkepentingan V= atau, v, W,…, unsur -unsur yang vektor. Dengan mereka beberapa operasi penting dijalankan, di antaranya yang berikut menonjol:

- Jumlah antara dua vektor u + v Akibatnya z, yang milik keseluruhannya V.

- Pendaraban nombor sebenar α oleh vektor v: α v yang memberikan vektor lain dan yang dimiliki V.

Visi artistik ruang vektor. Sumber: Pixabay

Untuk menunjukkan vektor kami menggunakan BOLD (v Ia adalah vektor), dan untuk skalar atau nombor huruf Yunani (α adalah nombor).

[TOC]

Aksioma dan sifat

Untuk menjadi ruang vektor, lapan aksioma seterusnya mesti dipenuhi:

1-conmutability: atau +v = v +atau

2-transitiviti: (atau + v) + W = atau + ( v + W)

3-kewujudan vektor null 0 seperti itu 0 + v = v

4-kewujudan sebaliknya: sebaliknya v adalah (-v) , Memandangkan itu v + (-v) = 0

5-produk pengedaran berkenaan dengan jumlah vektor: α ( atau + v ) = αatau +αv

6-produk pengedaran berkenaan dengan jumlah skalar: (α + β)v = αv +βv

7-Persatuan Produk Skalar: α (β v) = (α β)v

8-nombor 1 Ia adalah elemen neutral sejak: 1v = v

Contoh ruang vektor

Contoh 1

Vektor dalam satah (R²) adalah contoh ruang vektor. Vektor dalam satah adalah objek geometri yang mempunyai magnitud dan arah. Ia diwakili oleh segmen berorientasikan yang dimiliki oleh pesawat tersebut dan dengan saiz berkadar dengan magnitudnya.

Jumlah dua vektor dalam satah boleh ditakrifkan sebagai operasi geometri vektor kedua selepas yang pertama. Hasil jumlahnya adalah segmen berorientasikan yang bermula dari asal usul yang pertama dan mencapai hujung yang kedua.

Dalam angka itu dapat diperhatikan bahawa jumlah dalam r² adalah komutatif.

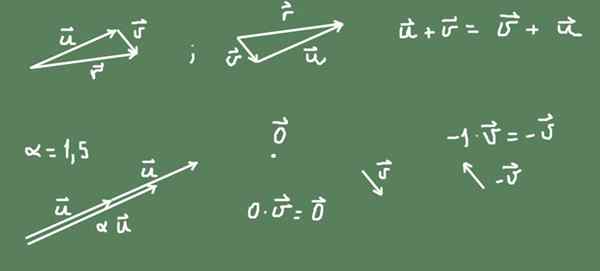Rajah 2. Vektor dalam ruang vektor bentuk kapal terbang. Sumber: Diri Diri.

Produk nombor α juga ditakrifkan oleh vektor. Sekiranya bilangannya positif, alamat vektor asal dikekalkan dan saiznya adalah α kali vektor asal. Sekiranya bilangannya negatif, alamatnya adalah sebaliknya, dan saiz vektor yang dihasilkan adalah nilai mutlak nombor.

Vektor menentang vektor v adalah -v = (-1) v.

Vektor null adalah titik dalam satah R², dan nombor sifar oleh vektor menghasilkan vektor null.

Semua berkata digambarkan dalam Rajah 2.

Contoh 2

Tetapkan P Dari semua polinomial kurang daripada atau sama dengan dua, termasuk gred sifar, mereka membentuk satu set yang memenuhi semua aksioma ruang vektor.

Ia boleh melayani anda: Peristiwa yang saling eksklusif: Contoh dan Contohnya

Menjadi polinomial p (x) = a x² + b x + c y q (x) = d x² + e x + f

Jumlah dua polinomial ditakrifkan: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Jumlah polinomial milik keseluruhannya P Ia adalah komutatif dan transitif.

Polinomial null milik keseluruhan P Ia adalah satu yang mempunyai semua pekali sama dengan sifar:

0 (x) = 0 x² + 0 x + 0

Jumlah skalar α ditakrifkan oleh polinomial seperti: α p (x) = α ∙ a x² + α ∙ b x + α ∙ c

Polinomial bertentangan P (x) ialah -p (x) = (-1) p (x).

Dari semua perkara di atas ia mengikuti bahawa set P Dari semua polinomial kurang daripada atau sama dengan dua, ia adalah ruang vektor.

Contoh 3

Tetapkan M Dari semua matriks M Rows X N Columns yang unsur -unsurnya adalah nombor sebenar membentuk ruang vektor sebenar, berkenaan dengan jumlah matriks dan produk dari nombor dengan matriks.

Contoh 4

Set f fungsi berterusan pemboleh ubah sebenar, membentuk ruang vektor, kerana jumlah dua fungsi dapat ditakrifkan, pendaraban skalar dengan fungsi, fungsi null dan fungsi simetri. Mereka juga memenuhi aksioma yang mencirikan ruang vektor.

Asas dan dimensi ruang vektor

Asas

Satu set vektor bebas linear ditakrifkan sebagai asas ruang vektor sedemikian rupa sehingga dari gabungan linear mereka mana -mana vektor ruang vektor dapat dihasilkan.

Menggabungkan dua atau lebih vektor secara linear terdiri daripada mendarabkan vektor oleh beberapa skalar dan kemudian menambahkannya secara vektor.

Sebagai contoh, dalam ruang vektor vektor dalam tiga dimensi yang dibentuk oleh r³ asas kanonik yang ditakrifkan oleh vektor unit (magnitud 1) digunakan (magnitud 1) Yo, J, k.

Di mana Yo = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Ini adalah vektor kartesian atau kanonik.

Mana -mana vektor V kepunyaan R³ ditulis sebagai V = a Yo + b J + c k, yang merupakan gabungan linear vektor asas Yo, J, k. Skalar atau nombor a, b, c dikenali sebagai komponen cartesian V.

Ia juga mengatakan bahawa vektor asas ruang vektor membentuk satu set ruang vektor.

Dimensi

Dimensi ruang vektor adalah nombor kardinal asas vektor untuk ruang tersebut; iaitu bilangan vektor yang membentuk asas tersebut.

Kardinal ini adalah bilangan maksimum vektor bebas linear dari ruang vektor itu, dan pada masa yang sama bilangan minimum vektor yang membentuk satu set penjanaan ruang tersebut.

Boleh melayani anda: Penduduk statistik: konsep, jenis, contoh

Pangkalan ruang vektor tidak unik, tetapi semua pangkalan ruang vektor yang sama mempunyai dimensi yang sama.

Subspace vektor

Subspace vektor ruang vektor v adalah subset v di mana operasi yang sama ditakrifkan seperti dalam v dan memenuhi semua aksioma ruang vektor. Oleh itu, subspace juga akan menjadi ruang vektor.

Contoh Subspace Vektor adalah vektor yang tergolong dalam pesawat XY. Subspace ini adalah subset ruang vektor dimensi yang lebih besar daripada set vektor milik ruang tiga dimensi xyz.

Satu lagi contoh vektor subspace s1 ruang vektor dibentuk oleh semua matriks 2 × 2 dengan elemen sebenar adalah yang ditakrifkan di bawah:

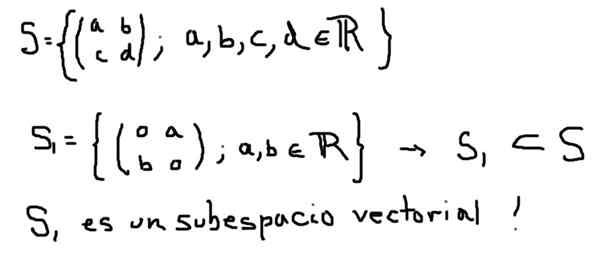
Sebaliknya, S2 ditakrifkan di bawah, walaupun ia adalah subset s, ia tidak membentuk ruang vektor:

Latihan yang diselesaikan

-Latihan 1

Jadilah vektor V1= (1, 1, 0); V2= (0, 2, 1) dan V3= (0, 0, 3) dalam r³.

a) membuktikan bahawa mereka bebas secara linear.

b) Buktikan bahawa mereka membentuk pangkalan dalam r³, kerana mana -mana senarai (x, y, z) boleh ditulis sebagai gabungan linear V1, V2, v3.

c) Cari komponen senarai V = (-3,5,4) di pangkalan V1, V2, V3.

Penyelesaian

Kriteria untuk menunjukkan kebebasan linear adalah untuk menubuhkan set persamaan berikut dalam α, β dan γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

Sekiranya satu -satunya penyelesaian untuk sistem ini ialah α = β = γ = 0 maka vektor secara linear bebas, jika tidak, mereka tidak.

Untuk mencapai nilai α, β dan γ kami mencadangkan sistem persamaan berikut:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Yang pertama membawa kepada α = 0, kedua α = -2 ∙ β tetapi sebagai α = 0 kemudian β = 0. Persamaan ketiga menunjukkan bahawa γ = (-1/3) β, tetapi sebagai β = 0 kemudian γ = 0.

Jawapan kepada

Disimpulkan bahawa ia adalah satu set vektor bebas linear di R³ .

Jawab b

Sekarang mari kita tulis senarai (x, y, z) sebagai gabungan linear V1, V2, v3.

(x, y, z) = α v1 + β v2 + γ v3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Ia boleh melayani anda: Ujian Tukey: Apa, dalam hal contoh, diselesaikan senaman

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Di mana anda mempunyai:

α = x

α + 2 β = y

β + 3 γ = z

Yang pertama menunjukkan α = x, kedua β = (y-x)/2 dan γ ketiga (z- y/2 +x/2)/3. Dengan cara ini, kami telah menemui penjana α, β dan γ dari mana -mana senarai R³ 

Jawab c

Mari cari komponen senarai V = (-3,5,4) di pangkalan V1, V2, V3.

Kami menggantikan nilai yang sepadan dalam ungkapan yang terdapat di atas untuk penjana.

Dalam kes ini kita ada: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

Itu dia:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Akhirnya:

V = -3 V1 + 4 V2 + 0 V3

Kami menyimpulkan bahawa V1, v2, v3 Mereka membentuk pangkalan di ruang vektor r³ dimensi 3.

-Latihan 2

Ekspres Polynomial P (T) = T² + 4T -3 sebagai gabungan linear P1 (t) = t² -2t + 5, p2 (t) = 2t² -3t dan p3 (t) = t + 3.

Penyelesaian

P (t) = x p1 (t) + dan p2 (t) + z p3 (t)

di mana nombor x, y, z mesti ditentukan.

Dengan mengalikan dan mengumpulkan istilah dengan tahap yang sama dalam t ia diperolehi:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Yang membawa kita ke sistem persamaan berikut:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Penyelesaian sistem persamaan ini adalah:

x = -3, y = 2, z = 4.

Itu dia:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Latihan 3

Tunjukkan bahawa vektor V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) dan V3= (2, 1, -1, 1) R⁴ adalah bebas secara linear.

Penyelesaian

Kami menggabungkan tiga vektor secara linear V1, V2, V3 Dan kami menuntut bahawa gabungan menambah elemen null r⁴

ke V1 + b V2 + c V3 = 0

Iaitu,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

Ini membawa kita ke sistem persamaan berikut:

A + B + 2 C = 0

B + C = 0

-A - C = 0

2 a + b + c = 0

Mengurangkan yang pertama dan keempat kita ada: -a + c = 0 Apa yang bermaksud a = c.

Tetapi jika kita melihat persamaan ketiga, kita perlu = -c. Satu-satunya cara untuk memenuhi A = C = (-c) ialah C adalah 0 dan oleh itu juga akan menjadi 0.

A = C = 0

Jika kita menggantikan hasil ini dalam persamaan pertama maka kita menyimpulkan bahawa b = 0.

Akhirnya a = b = c = 0, jadi dapat disimpulkan bahawa vektor v1, v2 dan v3 secara linear bebas.

Rujukan

1. Lipschutz, s. 1993. Algebra linear. Edisi kedua. McGraw - Hill. 167 - 198.