Ciri -ciri Faktor Biasa, Contoh, Latihan

Dia faktor biasa ungkapan algebra adalah jumlah yang ada dalam semua syarat ini. Apabila faktor biasa diketahui, adalah mungkin untuk menulis ungkapan dengan cara yang sama melalui produk faktor.

Tidak semua ungkapan algebra mempunyai faktor yang sama, hanya ada yang hanya dapat dibahagikan antara mereka dan 1, oleh itu tidak mungkin untuk menulisnya sebagai produk faktor. Contoh ungkapan yang tidak mempunyai faktor yang sama ialah:

x + y

Rajah 1. Faktor umum ekspresi algebra menjadikannya produk yang ditunjukkan dari dua faktor. Sumber: Pixabay.

Sebaliknya ini ya:

5a + 10b

Dilihat bahawa 5 hadir dalam kedua -dua istilah, kerana 10 = 5 ∙ 2. Oleh kerana 5 adalah faktor biasa, maka yang berikut boleh ditulis:

5a + 10b = 5 ∙ (A + 2b)

Pembaca boleh menyemak melalui harta pengedaran, bahawa ungkapan di sebelah kanan adalah sama dengan yang asal.

Faktor biasa juga boleh literal atau gabungan nombor dan huruf, contohnya dalam 4x² - 2x. The x dan juga 2 Mereka adalah antara faktor dan ungkapan tetap sebagai produk:

4x² -2x = 2x ⋅ (x -1)

Kelebihan mencari faktor umum ekspresi dan menulisnya sebagai produk adalah bahawa ia hampir selalu mudah untuk beroperasi dengannya. Itulah sebabnya ia digunakan dalam banyak prosedur algebra dan pengiraan seperti:

-Apabila menyelesaikan persamaan, penyelesaiannya dengan cepat diturunkan apabila faktor biasa dijumpai.

-Apabila mengira had dengan ketidaktentuan, ini mungkin hilang dengan pemfaktoran dengan betul.

-Faktor yang sesuai juga memudahkan operasi dengan ekspresi algebra yang rasional, seperti jumlah dan penolakan.

[TOC]

Ciri -ciri faktor umum

Ciri -ciri utama faktor umum adalah seperti berikut:

-Ia boleh menjadi nombor, ungkapan algebra, atau gabungan kedua -duanya.

-Faktor umum mesti terkandung dalam setiap syarat ekspresi kepada faktor.

Boleh melayani anda: Fungsi Transenden: Jenis, Definisi, Hartanah, Contoh

-Mengikut jumlah terma yang terkandung di dalamnya, mungkin berlaku:

1. Faktor monomial biasa, jika faktor biasa adalah satu istilah,
2. Faktor binomial biasa jika anda mempunyai dua syarat dan
3. Faktor polinomial biasa, jika faktor biasa terdiri daripada beberapa istilah.

Cara Mencari Faktor Biasa Ekspresi Algebra?

Untuk mencari faktor umum yang ada dalam polinomial, anda perlu mengira pembahagi maksimum maksimum atau MCD koefisien berangka semua istilah, serta huruf atau literals setiap istilah dan memilih kuasa dengan sedikit eksponen.

Surat atau literal boleh dibentangkan sebagai monomial, binomial atau polinomial, seperti yang akan dilihat dalam contoh berikut.

Yang paling disyorkan untuk memahami proses mendapatkan faktor umum, adalah mengikuti contoh dan amalan menyelesaikan beberapa latihan dalam setiap kes.

Contoh faktor umum

Kita tidak boleh kehilangan hakikat bahawa matlamat faktor umum ditukar kepada ekspresi ke dalam produk yang ditunjukkan dari faktor. Kemudian kes yang paling relevan dianalisis:

Faktor monomial biasa

Anda mempunyai monomial berikut (ungkapan algebra tunggal):

2x²; 10x⁴dan; 100x⁶dan²

Apa yang boleh menjadi faktor umum kepada ketiga -tiga?

Bermula dengan koefisien berangka: 2, 10 dan 100, semuanya juga dan MCD mereka adalah 2. Bagi bahagian literal, pembolehubah x hadir dalam tiga istilah, dan kuasa terendah ialah x², Maka faktor umum adalah 2x².

Tiga istilah yang dicadangkan boleh ditulis sebagai produk faktor ini dengan cara ini:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²dan

100x⁶dan²= 2x²∙ 50x⁴dan²

Mengalikan faktor di sebelah kanan, dapat disahkan bahawa istilah kiri diperolehi.

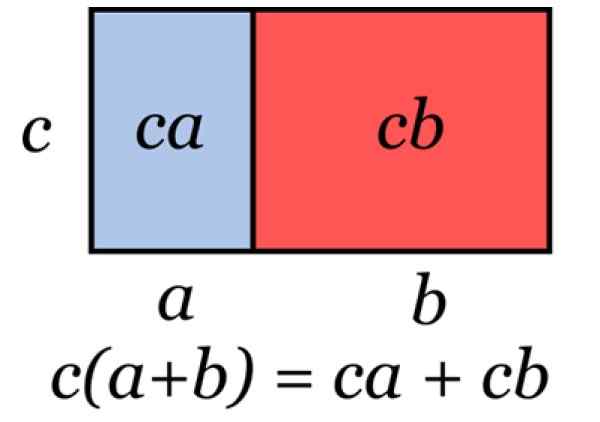Rajah 2. Ilustrasi yang mewakili faktor biasa. Sumber: Wikimedia Commons.

Teknik ini digunakan apabila diperlukan untuk memberi faktor ekspresi algebra, seperti dalam contoh berikut:

• Contoh 1

Fakta ungkapan berikut:

Ia dapat melayani anda: segitiga isosceles

5x³dan + 10x²dan² + 5xy²

MCD koefisien berangka setiap istilah adalah:

MCD (5.10) = 5

Bagi bahagian literal, kedua -dua x sebagai dan Mereka hadir dalam tiga syarat dan sekurang -kurangnya eksponen masing -masing adalah 1, oleh itu faktor umum adalah 5xy Dan anda boleh menulis:

5x³dan + 10x²dan² + 5xy²= 5xy ∙ (x² +2xy²+dan)

Faktor polinomial biasa

Faktor umum boleh terdiri daripada binomial, trinomial atau secara umum dalam polinomial. Dalam kes ini, arahan di bahagian sebelumnya masih sah, memilih sebagai faktor yang sama dengan eksponen yang sedikit.

• Contoh 2

Tulis ungkapan berikut sebagai produk dua faktor:

2a (x - 1) - 3b (x - 1)

Dengan pemeriksaan langsung, faktor umum adalah binomial (X-1), Jadi:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Pemfaktoran dengan mengumpulkan istilah

Kadang -kadang kewujudan faktor umum tidak jelas, tetapi ia diturunkan jika istilah dikumpulkan dengan cara yang mudah:

• Contoh 3

Faktor 3x³ - 9ax² - x + 3a

Pada pandangan pertama tidak ada faktor biasa dalam empat istilah ini, kerana contohnya x Ia hadir dalam tiga yang pertama, tetapi tidak pada yang terakhir. Dan juga ke Ia berada di tempat kedua dan yang terakhir tidak ada lagi.

Bagi koefisien, terdapat tiga istilah di mana 3 hadir, namun menjadi faktor yang sama, haruslah dalam semua istilah.

Nampaknya teknik yang diterangkan tidak dapat digunakan kali ini. Walau bagaimanapun, ungkapan itu boleh menjadi pemfaktoran dengan mengumpulkan dua istilah pertama dan dua yang terakhir, berhati -hati apabila meletakkan kurungan, bahawa tanda -tanda itu sesuai untuk tidak mengubah asal:

Boleh melayani anda: komponen segi empat tepat vektor (dengan latihan)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Perhatikan tanda negatif di tengah -tengah kurungan: ia perlu, kerana jika tidak, ungkapan asal akan berubah.

Dalam kurungan kiri faktor umum adalah 3x², Oleh itu:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

Dan diperhatikan bahawa faktor biasa telah muncul: (x - 3a), Iaitu, ia adalah faktor untuk kali kedua untuk mendapatkan:

3x² (x- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Latihan faktor umum

Latihan 1

Selesaikan persamaan 4x³ +7x²  +6x = 0

Penyelesaian

"X" adalah faktor biasa, oleh itu:

3x³ -5x²  +2x = x (3x² -5x +2) = 0

Untuk ungkapan di sebelah kiri, ia adalah 0, sudah cukup bahawa salah satu daripada dua syarat ini dipenuhi:

x = 0

Sama ada:

3x² -5x +2 = 0

Ini adalah persamaan darjah kedua lengkap yang dapat diselesaikan dengan menggunakan formula umum, juga dengan menggunakan kalkulator saintifik atau kaedah algebra lain. Penyelesaian persamaan ini adalah:

x = 1

x = 2/3

Setelah dijumpai, adalah ilustrasi untuk menulis persamaan sebagai produk dari 3 faktor, walaupun pernyataan itu tidak memintanya. Ia seperti ini:

x ⋅ (x-1) ⋅ (x-2/3) = 0

Latihan 2

Kirakan had berikut jika ada:

Penyelesaian

Pertama ia digantikan pada x = -2 untuk cuba menilai had, dengan berbuat demikian ia diperolehi:

Kerana ia adalah ketidaktentuan bentuk 0/0, anda harus menjadi faktor untuk cuba menghapuskannya. Penyebut tidak boleh menjadi faktor, tetapi pengangka itu.

Dalam pengangka faktor umum adalah x:

x²+2x = x ∙ (x+2)

Ekspresi yang difokuskan digantikan dengan had dan dengan cara ini ketidaktentuannya hilang:

Disimpulkan bahawa had wujud dan bernilai -2.

Rujukan

1. Baldor, a. 2005. Algebra. Kumpulan tanah air budaya.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Larson, r. 2012. Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
4. Stewart, J. 2007. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.