Aliran volumetrik

Kami menerangkan apa aliran volumetrik, bagaimana mengira dan faktor yang mempengaruhinya

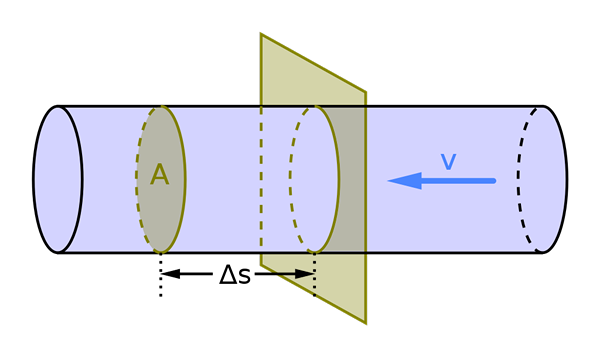
Aliran volumetrik bergantung kepada kawasan bahagian silang A dan kelajuan bendalir v. Sumber: Mikerun, CC BY-SA 4.0, melalui Wikimedia Commons

Apakah aliran volumetrik?

Dia aliran volumetrik Ia membolehkan untuk menentukan jumlah cecair yang melintasi bahagian saluran dan menawarkan ukuran kelajuan yang mana cecair bergerak dengan yang sama. Oleh itu, ukurannya sangat menarik di kawasan yang pelbagai seperti industri, perubatan, pembinaan dan penyelidikan, antara lain.

Walau bagaimanapun, mengukur kelajuan cecair (sama ada cecair, gas atau campuran kedua -duanya) tidak semudah kelajuan anjakan badan pepejal boleh mengukur. Oleh itu, ia berlaku untuk mengetahui kelajuan bendalir yang diperlukan untuk mengetahui alirannya.

Dari ini dan banyak isu lain yang berkaitan dengan cecair, cabang fizik yang dikenali sebagai tawaran mekanik bendalir. Aliran ini ditakrifkan sebagai bagaimana cecair seksyen saluran sedang berjalan, ia sudah menjadi saluran paip, saluran paip, sungai, saluran, aliran darah, dan lain -lain., dengan mengambil kira unit sementara.

Biasanya kelantangan bahawa kawasan tertentu dalam satu unit masa dikira, juga dipanggil aliran volumetrik. Aliran jisim atau jisim yang melintasi kawasan yang ditentukan pada masa tertentu juga ditakrifkan, walaupun ia digunakan kurang kerap daripada aliran volumetrik.

Bagaimana aliran volumetrik dikira?

Aliran volumetrik diwakili oleh huruf q. Bagi kes -kes di mana aliran bergerak tegak ke bahagian pemandu, ia ditentukan dengan formula berikut:

Q = A = V / T

Dalam formula ini, ia adalah bahagian pemandu (ia adalah kelajuan purata yang cecair mempunyai), v adalah jumlah dan masa t. Oleh kerana dalam sistem antarabangsa, kawasan atau bahagian pemandu diukur dalam m² Dan kelajuan dalam m/s, aliran diukur m³/s.

Boleh melayani anda: 21 peristiwa penting fizik

Bagi kes -kes di mana kelajuan anjakan bendalir menghasilkan sudut θ dengan arah tegak lurus ke bahagian permukaan A, ungkapan untuk menentukan aliran adalah seperti berikut:

Q = A cos θ

Ini selaras dengan persamaan sebelumnya, kerana apabila alirannya berserenjang dengan kawasan a, θ = 0 dan, oleh itu, cos θ = 1.

Persamaan di atas hanya benar jika kelajuan bendalir seragam dan jika bahagian bahagiannya rata. Jika tidak, aliran volumetrik dikira melalui integral berikut:

Q = ∫∫_s V D s

Dalam ds integral ini ia adalah vektor permukaan, ditentukan oleh ungkapan berikut:

Ds = n ds

Di sana, n adalah vektor unit biasa ke permukaan saluran dan ds elemen permukaan pembezaan.

Persamaan kesinambungan

Ciri -ciri cecair yang tidak dapat dikompresikan ialah jisim cecair dipelihara dengan dua bahagian. Inilah sebabnya persamaan kesinambungan dipenuhi, yang mewujudkan hubungan berikut:

ρ₁ Ke₁ V₁ = ρ₂ Ke₂ V₂

Dalam persamaan ini ρ adalah ketumpatan bendalir.

Bagi kes -kes rejim dalam aliran kekal, di mana ketumpatan adalah malar dan, oleh itu, ia dipenuhi bahawa ρ₁ = ρ₂, Ia dikurangkan kepada ungkapan berikut:

Ke₁ V₁ = A₂ V₂

Ini bersamaan dengan mengesahkan bahawa aliran dipelihara dan, oleh itu:

Q₁ = Q₂.

Dari pemerhatian di atas, ia mengikuti bahawa cecair mempercepatkan apabila mereka mencapai bahagian sempit saluran, sementara mereka mengurangkan kelajuan mereka ketika mereka mencapai seksyen yang lebih luas dari saluran. Fakta ini mempunyai aplikasi praktikal yang menarik, kerana ia membolehkan bermain dengan kelajuan anjakan cecair.

Boleh melayani anda: zarah subatomik

Prinsip Bernoulli

Prinsip Bernoulli menentukan bahawa untuk cecair yang ideal (ia.

Akhirnya, prinsip Bernoulli tidak lain -lain selain daripada perumusan undang -undang pemuliharaan tenaga untuk aliran cecair. Oleh itu, persamaan Bernoulli boleh dirumuskan seperti berikut:

H +V² / 2g+p/ ρg = tetap

Dalam persamaan ini h ialah ketinggian dan g adalah pecutan graviti.

Dalam persamaan Bernoulli, tenaga cecair diambil kira pada bila -bila masa, tenaga yang terdiri daripada tiga komponen.

• Komponen kinetik yang merangkumi tenaga, kerana kelajuan yang mana cecair bergerak.
• Komponen yang dihasilkan oleh potensi graviti, sebagai akibat dari ketinggian di mana cecair terletak.
• Komponen tenaga aliran, yang merupakan tenaga yang cecair mempunyai tekanan.

Dalam kes ini, persamaan Bernoulli dinyatakan seperti berikut:

H ρ g +(v² ρ)/2 + p = malar

Secara logiknya, dalam hal cecair sebenar ekspresi persamaan Bernoulli tidak dipenuhi, karena dalam perpindahan bendalir ada kerugian geseran dan perlu untuk menggunakan persamaan yang lebih kompleks.

Apa yang mempengaruhi aliran volumetrik?

Aliran volumetrik akan terjejas jika terdapat halangan di saluran.

Boleh melayani anda: Pembiasan cahaya: Unsur, undang -undang dan percubaan

Di samping itu, aliran volumetrik juga boleh berubah dengan kesan suhu dan suhu variasi tekanan dan tekanan yang mana.

Kaedah mudah mengukur aliran volumetrik

Kaedah yang sangat mudah untuk mengukur aliran volumetrik adalah untuk membiarkan aliran bendalir dalam tangki pengukuran untuk jangka waktu tertentu.

Kaedah ini biasanya tidak begitu praktikal, tetapi kebenarannya adalah sangat mudah dan sangat ilustrasi untuk memahami makna dan kepentingan mengetahui aliran cecair.

Dengan cara ini, bendalir dibenarkan mengalir ke dalam tangki pengukuran untuk tempoh masa, jumlah terkumpul diukur dan hasil yang diperoleh antara masa berlalu dibahagikan.

Rujukan

1. Aliran (cecair) (n.d.).  Di Wikipedia. Pulih dari ES.Wikipedia.org.
2. Kadar aliran volumetrik (n.d.).  Di Wikipedia. Diambil dari.Wikipedia.org.
3. Jurutera Edge, LLC. "Persamaan Kadar Aliran Volumetrik Fluida". Jurutera tepi
4. Mott, Robert (1996). "1". Mekanik cecair yang digunakan (Edisi ke -4). Mexico: Pendidikan Pearson.
5. Batchelor, g.K. (1967). Pengenalan kepada Dinamika Fluida. Cambridge University Press.
6. Landau, l.D.; Lifshitz, e.M. (1987). Mekanik cecair. Kursus Fizik Teoritis (ed 2.). Pergamon Press.