Fungsi Ciri -ciri Malar, Contoh, Latihan

The fungsi malar Ia adalah satu di mana nilai dan. Dengan kata lain: fungsi tetap selalu mempunyai bentuk  f (x) = k, di mana k Ia adalah nombor sebenar.

Dengan menggambarkan fungsi malar dalam sistem koordinat Xy, Ia selalu selari lurus selari dengan paksi mendatar atau paksi x.

Rajah 1. Graf beberapa fungsi berterusan pada pesawat Cartesian. Sumber: Wikimedia Commons. Pengguna: Hite [Domain Awam]

Fungsi ini adalah kes tertentu fungsi berkaitan, graf yang juga garis lurus, tetapi dengan cerun. Fungsi tetap mempunyai null yang belum selesai, iaitu, ia adalah garis mendatar, seperti yang dilihat dalam Rajah 1.

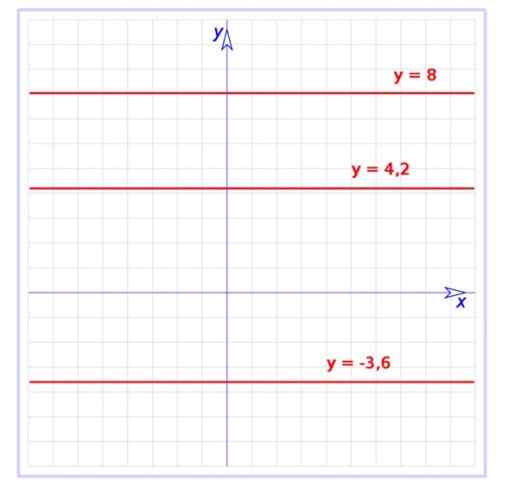
Terdapat graf tiga fungsi berterusan:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Semua selari lurus dengan paksi mendatar, yang pertama adalah di bawah paksi, sementara yang tinggal di atas.

[TOC]

Ciri -ciri fungsi berterusan

Kita dapat meringkaskan ciri -ciri utama fungsi malar seperti berikut:

-Grafnya adalah garis lurus mendatar.

-Ia mempunyai persimpangan yang unik dengan paksi dan, bernilai k.

-Ia berterusan.

-Penguasaan fungsi malar (set nilai yang x) adalah set nombor sebenar R.

-Laluan, julat atau percanggahan (set nilai yang diperlukan oleh pembolehubah dan) hanya tetap k.

Contoh

Fungsi diperlukan untuk mewujudkan hubungan antara magnitud yang bergantung pada satu sama lain dalam beberapa cara. Hubungan yang ada di antara mereka boleh dimodelkan secara matematik, untuk mengetahui bagaimana salah satu daripada mereka berkelakuan apabila yang lain berbeza.

Boleh melayani anda: papomudas

Ini membantu membina model untuk banyak situasi dan membuat ramalan mengenai tingkah laku dan evolusi mereka.

Walaupun kesederhanaannya yang jelas, fungsi tetap mempunyai banyak aplikasi. Contohnya, ketika mempelajari magnitud yang tetap tetap dalam waktu, atau sekurang -kurangnya, untuk waktu yang cukup.

Dengan cara ini, magnitud berkelakuan dalam situasi seperti yang berikut:

-The kelajuan Pelayaran kereta yang bergerak di lebuh raya rectilinear yang panjang. Selagi ia tidak berhenti atau mempercepatkan, kereta membawa pergerakan rectilinear seragam.

Rajah 2. Sekiranya kereta tidak berhenti atau mempercepatkan, ia mempunyai pergerakan rectilinear seragam. Sumber: Pixabay.

-Pemeluwap yang dimuatkan dan terputus dari litar, mempunyai beban tetap dalam masa.

-Akhirnya, tempat letak kereta rata, mengekalkan a harga tetap tidak kira berapa lama kereta yang diletakkan di sana.

Cara lain untuk mewakili fungsi yang berterusan

Fungsi malar secara bergantian boleh diwakili seperti berikut:

f (x) = kx⁰

Sejak nilai dari x Dibesarkan kepada 0 memberikan 1 hasilnya, ungkapan sebelumnya dikurangkan kepada yang biasa:

f (x) = k

Sudah tentu itu berlaku selagi nilai k berbeza dengan 0.

Itulah sebabnya fungsi tetap juga diklasifikasikan sebagai fungsi polinomial Gred 0, sejak eksponen pembolehubah x Ia adalah 0.

Latihan yang diselesaikan

- Latihan 1

Jawab soalan berikut:

a) Bolehkah ia disahkan bahawa garis yang diberikan oleh x = 4 adalah fungsi malar? Alasan jawapan anda.

b) Bolehkah fungsi tetap mempunyai persimpangan dengan paksi x?

c) Adakah fungsi f (x) = w tetap²?

Jawapan kepada

Berikut adalah graf garis x = 4:

Boleh melayani anda: Pembolehubah statistik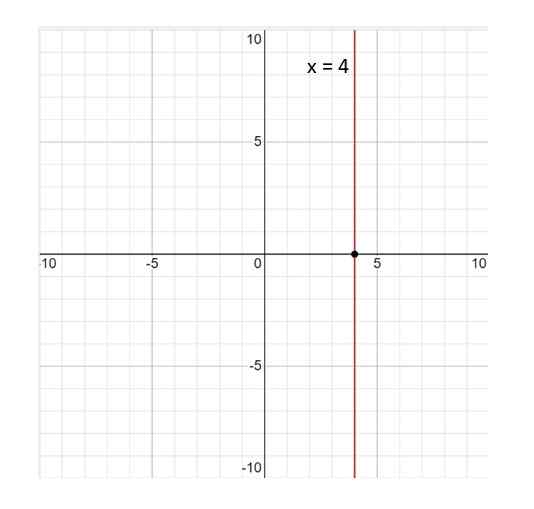 Rajah 3. Graf garis x = 4. Sumber: f. Zapata.

Barisan x = 4 bukan fungsi; Dengan definisi fungsi adalah hubungan sedemikian rupa sehingga setiap nilai pembolehubah x Ia sepadan dengan satu nilai dari dan. Dan dalam kes ini ini tidak dipenuhi, kerana nilai x = 4 dikaitkan dengan nilai tak terhingga dan. Oleh itu jawapannya tidak.

Jawab b

Secara umum, fungsi malar tidak mempunyai persimpangan dengan paksi x, Kecuali ia y = 0, di mana ia adalah paksi x Kata dengan betul.

Jawab c

Ya, sejak W Ia tetap, persegi juga. Apa minatnya W Ia tidak bergantung pada pemboleh ubah input x.

- Latihan 2

Cari persimpangan antara fungsi f (x) = 5 dan G (x) = 5x - 2

Penyelesaian

Untuk mencari persimpangan antara kedua -dua fungsi ini, mereka boleh ditulis semula sebagai:

y = 5; y = 5x - 2

Mereka dipadankan, memperoleh:

5x - 2 = 5

Yang merupakan persamaan linear darjah pertama, yang penyelesaiannya adalah:

5x = 5+2 = 7

x = 7/5

Titik persimpangan adalah (7/5; 5).

- Latihan 3

Menunjukkan bahawa yang diperoleh dari fungsi tetap adalah 0.

Penyelesaian

Dari definisi derivatif yang anda ada:

 f (x) = k

f (x+h) = k

Menggantikan definisi:

Di atas masuk akal, kerana derivatif fungsi ditakrifkan sebagai cerun garis tangen ke lengkung pada titik tertentu. Fungsi tetap mempunyai null yang belum selesai dan garis tangen juga.

Di samping itu, jika kita berfikir tentang derivatif sebagai kadar pertukaran Dy/dx, Fungsi malar tidak mengalami perubahan, oleh itu derivatifnya tidak sah.

Boleh melayani anda: Prinsip Multiplicative: Mengira Teknik dan Contoh

- Latihan 4

Cari integral tak terbatas dari f (x) = k.

Penyelesaian

- Latihan 5

Syarikat telefon bimbit menawarkan perkhidmatan internet tanpa had dengan kadar rata membayar $ 15 sebulan. Berapakah fungsi harga mengikut masa?

Penyelesaian

Biarkan p menjadi harga yang akan dibayar pada masa $ dan t, yang boleh dinyatakan dalam beberapa hari. Fungsi ini ditubuhkan seperti berikut:

P (t) = 15

- Latihan 6

Graf versus masa berikut sepadan dengan pergerakan zarah.

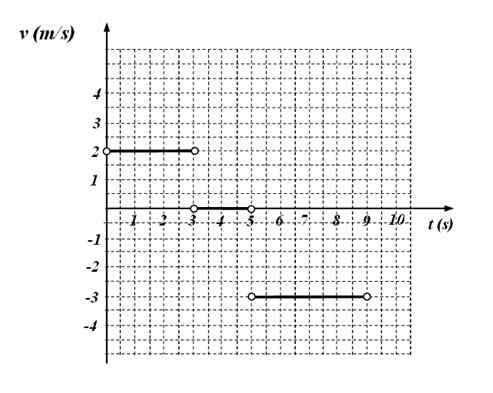Rajah 4. Fungsi V (t) Grafik Fungsi untuk Latihan 6. Sumber: f. Zapata.

Ia diminta:

a) Tulis ungkapan untuk fungsi kelajuan sebagai fungsi masa V (t).

b) Cari jarak yang dilalui oleh mudah alih dalam selang waktu antara 0 dan 9 saat.

Penyelesaian kepada

Graf yang menunjukkan bahawa:

-V = 2 m/s Dalam selang waktu antara 0 dan 3 saat

-Mudah alih ditahan antara 3 dan 5 saat, kerana dalam selang ini kelajuan bernilai 0.

-V = - 3 m/s Antara 5 dan 9 saat.

Ini adalah contoh sekeping kepingan, atau fungsi di bahagian -bahagian, yang pada gilirannya terdiri daripada fungsi malar, hanya sah untuk selang waktu yang ditunjukkan. Disimpulkan bahawa fungsi yang dicari adalah:

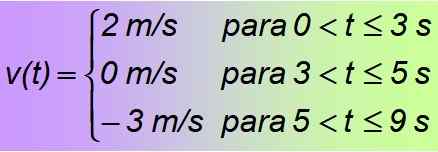
Penyelesaian b

Dari graf v (t) jarak yang dilalui oleh mudah alih boleh dikira, yang secara numerik sama dengan kawasan rendah/pada lengkung. Cara ini:

-Jarak perjalanan antara 0 dan 3 saat = 2 m/s . 3 s = 6 m

-Antara 3 dan 5 saat dia ditahan, oleh itu dia tidak melakukan perjalanan jarak jauh.

-Jarak perjalanan antara 5 dan 9 saat = 3 m/s . 4 s = 12 m

Dalam jumlah mudah alih yang melawat 18 m. Lihat bahawa walaupun kelajuan negatif dalam selang antara 5 dan 9 saat, jarak perjalanan adalah positif. Apa yang berlaku ialah pada selang masa itu, mudah alih telah mengubah makna kelajuannya.

Rujukan

1. Geogebra. Fungsi berterusan. Pulih dari: geogra.org.
2. Maplesoft. Fungsi malar. Pulih dari: Maplesoft.com.
3. Wikilibros. Pengiraan dalam pemboleh ubah/fungsi/fungsi malar. Pulih dari: Adakah.Wikibooks.org.
4. Wikipedia. Fungsi malar. Diperoleh dari: dalam.Wikipedia.org
5. Wikipedia. Fungsi malar. Pulih dari: Adakah.Wikipedia.org.