Fungsi homografi bagaimana graf, latihan yang diselesaikan

The fungsiHomografi atau rasional Ón Ia adalah sejenis fungsi matematik yang terdiri daripada pembahagian dua komponen polinomial. Ia mematuhi bentuk p (x)/q (x), di mana q (x) tidak dapat mengambil bentuk null.

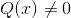
Contohnya ungkapan (2x - 1)/(x + 3) sepadan dengan fungsi homografi dengan p (x) = 2x - 1 y q (x) = x + 3.

Sumber: Pixabay.com

Fungsi homografi merupakan bahagian kajian fungsi analisis, yang dirawat dari pendekatan grafik dan dari kajian domain dan pelbagai. Ini disebabkan oleh sekatan dan asas yang mesti digunakan untuk resolusi mereka.

[TOC]

Apa itu fungsi homografi?

Mereka adalah ungkapan rasional pemboleh ubah yang unik, walaupun ini tidak bermakna bahawa tidak ada ekspresi yang sama untuk dua atau lebih pembolehubah, di mana ia akan berada di hadapan badan di ruang yang mematuhi corak yang sama seperti fungsi homografi di peringkat.

Mereka mempunyai akar sebenar dalam beberapa kes, tetapi kewujudan asymptot menegak dan mendatar sentiasa dikekalkan, serta juga pertumbuhan dan penurunan selang waktu. Biasanya hanya satu daripada trend ini, tetapi terdapat ungkapan yang mampu menunjukkan kedua -duanya dalam perkembangan mereka.

Domainnya dihadkan oleh akar penyebut, kerana tidak ada pembahagian antara sifar nombor nyata.

Fungsi homografi campuran

Mereka sangat kerap dalam pengiraan, terutamanya perbezaan dan komprehensif, yang diperlukan untuk memperoleh dan anti -Angel di bawah formula tertentu. Beberapa yang paling biasa diklasifikasikan di bawah.

Sepasang fungsi homografi n

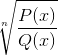
Tidak termasuk semua elemen domain yang menjadikan argumen negatif. Akar yang terdapat dalam setiap polinomial menunjukkan nilai sifar apabila dinilai.

Nilai -nilai ini diterima oleh radikal, walaupun sekatan asas fungsi homografi harus dipertimbangkan. Di mana q (x) tidak dapat menerima nilai null.

Boleh melayani anda: Fungsi Transenden: Jenis, Definisi, Hartanah, Contoh

Penyelesaian selang mesti dipintas:

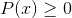
Untuk mencapai persimpangan, kaedah tanda boleh digunakan, antara lain.

Logaritma fungsi homografi

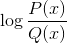
Tidak termasuk nilai domain yang membuang selang negatif dan sifar. Kerana sifar telah dikecualikan daripada penyebut, penyelesaian: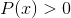

Ia juga biasa untuk mencari kedua -dua ungkapan dalam satu, antara kombinasi lain yang mungkin.

Cara Grafik Fungsi Homografi?

Fungsi homografi sesuai dengan grafik dengan hiperbola dalam pesawat. Yang diangkut secara mendatar dan menegak mengikut nilai -nilai yang menentukan polinomial.

Terdapat beberapa elemen yang mesti kita tentukan untuk menggambarkan fungsi rasional atau homografi.

Estet

Yang pertama adalah akar atau sifar fungsi p dan q.

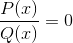
Nilai yang dicapai akan dilambangkan pada paksi x grafik. Menunjukkan persimpangan graf dengan paksi.

Asymptote menegak

Sesuai dengan garis menegak, yang menonjolkan graf mengikut trend yang mereka sampaikan. Mereka menyentuh paksi x dalam nilai -nilai yang menjadikan penyebut sifar dan tidak akan disentuh oleh graf fungsi homografi.

Asymptote mendatar

Diwakili oleh garis jahitan mendatar, menandakan had yang mana fungsi itu tidak akan ditakrifkan pada titik yang tepat. Trend akan diperhatikan sebelum dan selepas garis ini.

Untuk mengira ia, kita mesti menggunakan kaedah yang serupa dengan kaedah l'oply, yang digunakan untuk menyelesaikan had fungsi rasional yang cenderung tak terhingga. Koefisien kuasa tertinggi dalam pengangka dan penyebut fungsi mesti diambil.

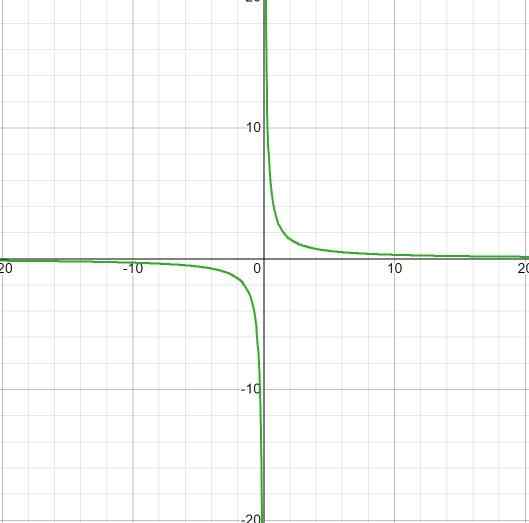
Sebagai contoh, ungkapan berikut mempunyai asymptote mendatar pada y = 2/1 = 2.

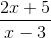
Selang pertumbuhan

Nilai yang diperintahkan akan mempunyai trend yang ditandakan dalam graf kerana asymptotes. Dalam hal pertumbuhan, fungsi akan meningkat dari nilai kerana unsur -unsur domain dari kiri ke kanan dinilai.

Boleh melayani anda: 60 pembahagi

Penurunan selang

Nilai yang diperintahkan akan berkurangan kerana unsur -unsur domain dari kiri ke kanan dinilai.

Lompatan yang terdapat dalam nilai -nilai tidak akan diambil kira apabila kenaikan atau berkurangan. Ini berlaku apabila graf hampir dengan menegak atau mendatar.

Persimpangan dengan y

Membuat sifar nilai x, adalah persimpangan dengan paksi ordinat. Ini adalah fakta yang sangat berguna untuk mendapatkan graf fungsi rasional.

Contoh

Tentukan graf ungkapan berikut, cari akarnya, asymptot menegak dan mendatar, pertumbuhan dan penurunan selang dan persimpangan dengan paksi yang diperintahkan.

Latihan 1

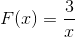
Ekspresi tidak mempunyai akar, kerana ia mempunyai nilai tetap dalam pengangka. Sekatan untuk memohon akan x berbeza dari sifar. Dengan asymptote mendatar pada y = 0, dan asymptote menegak pada x = 0. Tidak ada titik persimpangan dengan paksi dan.

Adalah diperhatikan bahawa tidak ada selang pertumbuhan walaupun dengan melompat dari kurang hingga lebih tak terhingga dalam x = 0.

Selang penurunan adalah

Id: (-∞; o) u (0, ∞)

Latihan 1.2

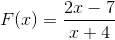
2 polinomial diperhatikan seperti dalam definisi awal, jadi kami meneruskan mengikut langkah -langkah yang ditetapkan.

Akar yang dijumpai adalah x = 7/2 yang disebabkan oleh menyamakan fungsi.

Asymptote menegak berada di x = - 4, yang merupakan nilai yang dikecualikan dari domain kerana keadaan fungsi rasional.

Asymptote mendatar berada dalam y = 2, ini selepas membahagikan 2/1, koefisien pembolehubah gred 1.

Ia mempunyai persimpangan dengan yang diperintahkan di y = - 7/4. Nilai yang dijumpai selepas menyamakan x ke sifar.

Ia boleh melayani anda: pecahan bersamaan dengan 3/5 (penyelesaian dan penjelasan)

Fungsi ini tumbuh secara berterusan, dengan lompatan dari lebih sedikit hingga tidak terhingga di sekitar akar x = -4.

Selang pertumbuhannya ialah ( -∞, - 4) u ( - 4, ∞).

Apabila nilai x hampir kurang tak terhingga, fungsi mengambil nilai hampir 2. Perkara yang sama berlaku apabila x mendekati lebih tak terhingga.

Ekspresi mendekati lebih tak terhingga apabila dinilai di - 4 di sebelah kiri, dan kurang tak terhingga apabila dinilai dalam - 4 di sebelah kanan.

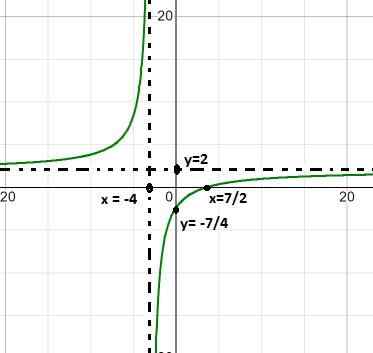
Latihan 2

Grafik fungsi homografi berikut diperhatikan:

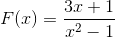
Terangkan tingkah laku, akar, asymptot menegak dan mendatar, pertumbuhan dan penurunan selang dan persimpangan dengan paksi yang diperintahkan.

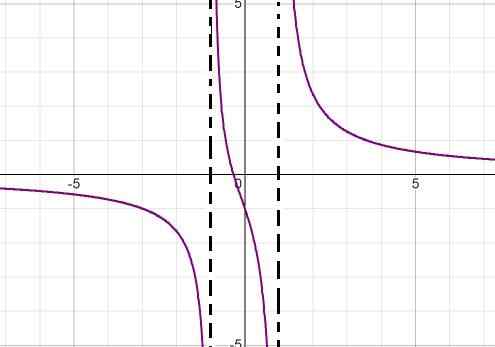
Penyebut ungkapan menunjukkan dengan memfokuskan perbezaan dataran (x + 1) (x - 1) nilai akar. Dengan cara ini kedua -dua asymptot menegak boleh ditakrifkan sebagai:

x = -1 dan x = 1

Asymptote mendatar sepadan dengan paksi abscissa kerana kuasa utama berada dalam penyebut.

Satu -satunya akar ditakrifkan oleh x = -1/3.

Ungkapan selalu berkurangan dari kiri ke kanan. Ia mendekati sifar apabila ia cenderung ke tak terhingga. Kurang tak terhingga ketika mendekati -1 di sebelah kiri. Lebih tak terhingga ketika mendekati -1 di sebelah kanan. Kurang tak terhingga ketika menghampiri 1 di sebelah kiri dan lebih tak terhingga ketika mendekati 1 di sebelah kanan.

Rujukan

1. Penghampiran dengan fungsi rasional. Donald J. Lelaki Baru. Soc Matematik Amerika., 31 Dis. 1979
2. Fungsi penarafan ortogonal. Universiti La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13 Feb. 1999
3. Penghampiran penarafan fungsi sebenar. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 Mac. 2011
4. Fungsi algebra. Gilbert Ames Bliss. Couer Corporation, 1 Jan. 2004
5. Majalah Masyarakat Matematik Sepanyol, 5-6 jilid. Persatuan Matematik Sepanyol, Madrid 1916