Fungsi ijazah lebih besar daripada dua (contoh)

A (polinomial) gred lebih besar daripada dua mempunyai bentuk umum:

f (x) = a₀ + ke₁x +a₂x² +… .ke_nxⁿ

Dengan n = 3, 4, 5, ..., integer bukan negatif dan koefisien ke_{Sama ada}, ke₁... ke_n, yang biasanya nombor sebenar.

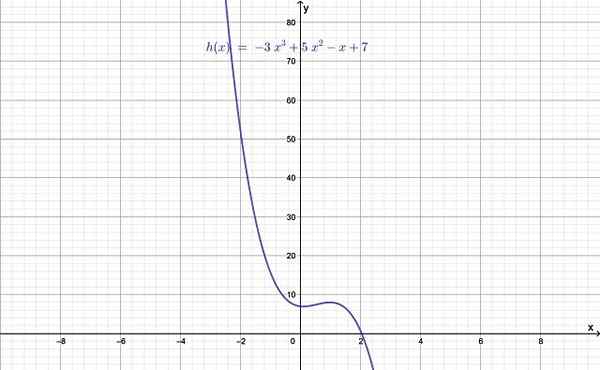Rajah 1.- Graf fungsi darjah lebih besar daripada 2. Sumber: f. Zapata.

Tahap fungsi diberikan oleh nilai n, yang terbesar dari eksponen dan yang seterusnya lebih besar daripada 2. Apabila n = 0 adalah fungsi malar, jika n = 1 ia adalah fungsi linear, dan akhirnya dengan n = 2 ia adalah fungsi kuadratik.

Contoh fungsi lebih besar daripada dua, dalam pembolehubah "x", adalah berikut:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Fungsi f (x) = x³ Ia adalah yang paling mudah dari semua fungsi yang lebih besar daripada dua dan ijazahnya adalah 3. Ijazah 3 juga dikenali sebagai fungsi padu. Bagi bahagiannya, g (x) adalah gred 4, kerana menjadi 4 eksponen maksimum.

Nilai n sangat penting kerana ia menentukan bentuk umum graf, dan juga jumlah maksimum akar atau persimpangan yang berfungsi dengan paksi mendatar. Sesungguhnya, fungsi 3 -grade akan menyentuh paksi mendatar paling banyak 3 mata, salah satu gred 4 akan melakukannya paling banyak dalam 4 mata dan sebagainya.

Bagi istilah bebas, dalam fungsi polinomial dari mana -mana darjah ia menunjukkan persimpangan fungsi dengan paksi menegak.

Ciri -ciri fungsi polinomial lebih besar daripada dua

Domain

Domain fungsi adalah set nilai yang membolehkan mengira nilai y = f (x). Untuk fungsi polinomial yang ditetapkan ini ialah nombor N sebenar, atau set nombor kompleks, jika perlu untuk melanjutkan domain.

Boleh melayani anda: Had Trigonometrik: Cara menyelesaikannya, Latihan Selesai

Bermaksud itu, memandangkan fungsi polinomial f (x) = a₀ + ke₁x +a₂x² +… .ke_nxⁿ, Anda sentiasa boleh menggantikan nombor sebenar, menjalankan operasi yang ditunjukkan dan dapatkan hasilnya nilai sebenar y = f (x) sebenar.

Julat

Ia adalah set yang dibentuk oleh semua nilai yang diperoleh f (x), iaitu imej yang setiap nilai x mempunyai melalui fungsi f (x). Untuk fungsi polinomial lebih besar daripada 2, set ini adalah nombor sebenar.

Akar fungsi

Adalah nilai x yang mana ia dipenuhi bahawa f (x) = 0. Seperti yang ditunjukkan di atas, tahap fungsi menunjukkan bilangan maksimum akar yang boleh dimiliki, walaupun tidak semuanya semestinya nyata.

Apabila pekali fungsi adalah nombor sebenar, akar sebenar sesuai dengan persimpangan fungsi dengan paksi x.

Contoh 1

Akar rasional fungsi f (x) = 2x³ - 9x² + 7x + 6 boleh didapati melalui teorem berikut:

Sekiranya akar f (x) = a₀ + ke₁x +a₂x² +… .ke_nxⁿ Ia adalah bentuk b/c, jadi nilai b yang mungkin adalah faktor a_{Sama ada} dan kemungkinan nilai c adalah faktor a_n.

Untuk fungsi contoh, kombinasi yang telah dipermudahkan ialah: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Sekarang masing -masing diuji melalui prosedur bahagian sintetik, contohnya. Apabila sisa pembahagian adalah 0, nilai yang terbukti adalah akar:

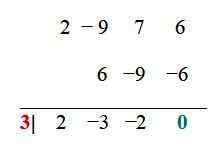
Nilai x₁ = 3 adalah akar atau sifar fungsi, oleh itu (x - 3) adalah faktor umum f (x), dan ini boleh ditulis sebagai:

Ia boleh melayani anda: lingkaran kesatuan: fungsi dan aplikasi trigonometri

f (x) = (x - 3) ∙ (2x² -3x -2)

Baki dua akar adalah nilai yang memenuhi persamaan 2x² -3x -2 = 0. Persamaan ini dapat diselesaikan melalui formula umum, kalkulator saintifik atau mengulangi proses Tanteo sebelumnya.

Akar ini adalah x₂ = 2 dan x₃ = - ½, dan sekarang f (x) boleh ditulis sebagai produk dari tiga faktor:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Persimpangan f (x) dengan paksi x adalah titik: p₁ (3.0), p₂(2.0) dan p₃(-½, 0). Grafik fungsi, yang diperoleh dengan geogebra, menunjukkan persimpangannya dengan paksi x:

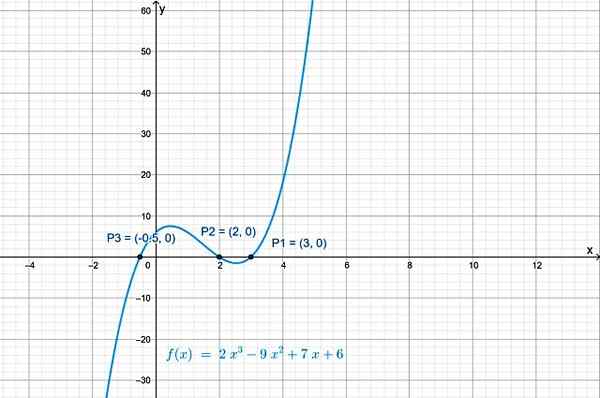Rajah 2.- Fungsi polinomial gred 3 mempunyai tiga persimpangan dengan paksi mendatar. Sumber: f. Zapata.

Persimpangan dengan paksi menegak

Untuk mencari persimpangan fungsi dengan paksi menegak yang anda perlukan untuk mencari f (0), yang semata -mata untuk₀.

Contoh 2

Cari persimpangan f (x) = 2x³ - 9x² + 7x + 6 dengan paksi menegak sangat mudah, ketika membuat x = 0 dalam f (x) ia diperolehi:

f (x) = 6

Dan titik persimpangan fungsi dengan paksi menegak adalah p₄(0.6).

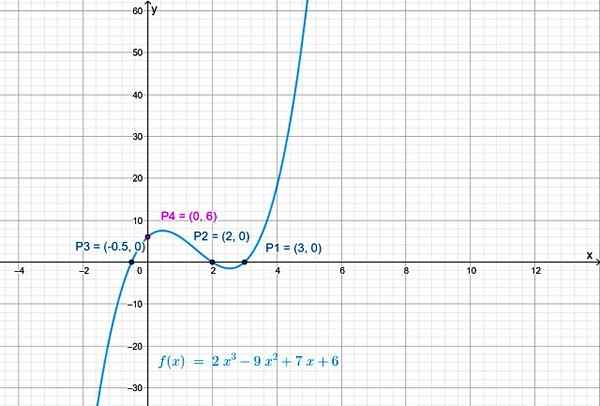Rajah 3. Persimpangan lengkung dengan paksi menegak membuat x = 0 dalam f (x). Sumber: f. Zapata.

Kesinambungan

Fungsi polinom secara umum, dan khususnya yang lebih tinggi daripada 2 adalah fungsi berterusan di seluruh domain mereka, ini bermakna mereka tidak mempunyai lompatan, langkah, lubang atau nilai yang tidak ditakrifkan. Mereka juga tidak mempunyai asymptotes, yang menegak, mendatar atau serong terus ke mana fungsi itu menghampiri tanpa menyeberanginya.

Kualiti kelembutan dan kesinambungan ini dihargai dalam graf yang ditunjukkan di atas.

Graf fungsi lebih tinggi daripada 2

Grafik fungsi yang lebih tinggi daripada 2 berterusan dan lembut, dan bentuknya bergantung pada tahap polinomial.

Boleh melayani anda: permutasi tanpa pengulangan: formula, demonstrasi, latihan, contoh

Sebagai contoh, mereka yang mempunyai gred 3 ia mempunyai tanda negatif dalam istilah dengan ijazah tertinggi).

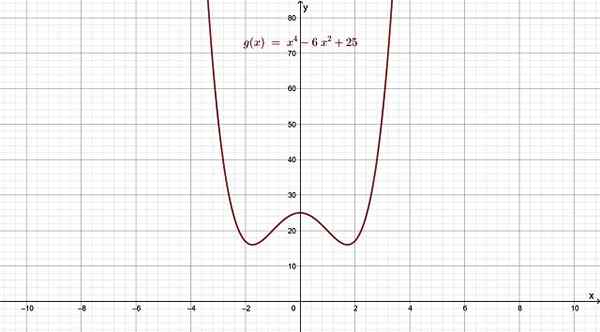Rajah 4. Fungsi poliomik gred 4, yang grafnya menyerupai huruf w. Sumber: f. Zapata.

Untuk nilai x jauh dari x = 0, kedua -dua kiri dan kanan, fungsi ini bertindak bagaimana istilah ijazah yang paling besar akan dilakukan, kerana ini berlaku di atas orang lain apabila x menjadi sangat besar atau sangat kecil.

Dalam imej yang mengikuti fungsi f (x) = 2x dibandingkan³ - 9x² + 7x + 6 dengan fungsi r (x) = x³ Dan dihargai bahawa bentuk kedua -dua lengkung adalah serupa dengan nilai x yang jauh dari x = 0.

Untuk nilai x yang besar, fungsi tumbuh dengan cepat dengan cenderung kepada +∞, manakala untuk nilai x negatif, fungsi berkurangan dengan cepat dan cenderung ke -∞.

Rajah 5.- Semua fungsi gred n berkelakuan sama ketika mereka berpindah dari x = 0, kedua -dua kiri dan kanan. Sumber: f. Zapata.

Membandingkan lengkung tork -grade (Rajah 4) dengan tahap ganjil (Rajah 2), selagi pekali yang mengiringi istilah gred tertinggi mempunyai tanda yang sama, diperhatikan bahawa lengkung darjah ganjil bermula dari "y" negatif dan negatif dan negatif dan negatif dan negatif dan berkembang, sementara gred sasaran bermula dalam "y" positif dan berkurangan.

Rujukan

1. Barnett, r. 2000. Preccculment: Fungsi dan Grafik. Ke -4. Edisi. McGraw Hill.
2. Pengiraan.DC. Fungsi polinom. Pulih dari: pengiraan.DC.
3. Larson, r. 2012. Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
4. Stewart, J. 2007. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Varsity Tutorrs. Grafik fungsi polinomial. Diperolehi dari: WarSityTorm.com.