Fungsi trigonometri asas, dalam pesawat Cartesian, contoh, senaman

The fungsi trigonometri Pemboleh ubah sebenar mereka sesuai dengan sudut (dinyatakan dalam radian), sebab trigonometri, yang boleh menjadi sinus, kosinus, tangen, cotangent, secant dan penuai.

Dengan cara ini kita mempunyai enam fungsi trigonometri: sinus, kosinus, tangen, penuai, pengeringan dan cotangent.

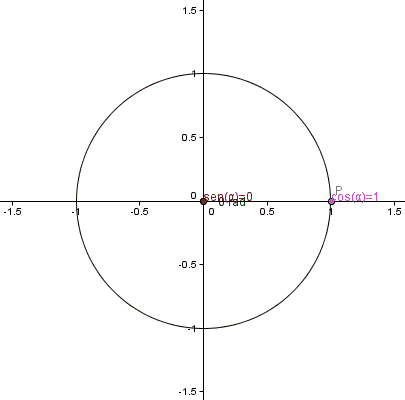Rajah 1. Animasi Circle Trigonometrik. Sumber: Wikimedia Commons.

Fungsi trigonometri untuk sudut antara 0 dan 2π ditakrifkan dengan bantuan lilitan kesatuan, radio 1 dan pusatnya bertepatan dengan asal -usul sistem koordinat Cartesian: titik (0.0).

Kita boleh mencari titik P koordinat (x, y) pada lilitan ini.

Segmen yang menyatukan asal dengan P, bersama -sama dengan segmen masing -masing yang menyatukan unjuran P pada paksi koordinat, membentuk segitiga segi empat tepat, yang alasan trigonometriknya dikenali sebagai kuota antara sisi segitiga. Jadi:

• sin θ = bertentangan /hypotenusa cateto
• cos θ = bersebelahan /hypotenusa Cateto
• Tg θ = bertentangan dengan Cateto /Cateto bersebelahan

Dan sekarang sebab -sebab yang terbalik di atas:

• Sec θ = Hypotenuse /Cateto bersebelahan
• Bahaya θ = hypotenusa /cateto bertentangan
• CTG θ = Cateto bersebelahan /bertentangan Cateto

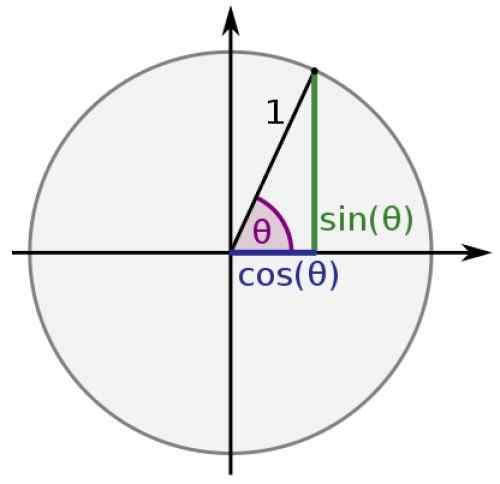
Dalam lingkaran kesatuan, hipotenus mana -mana segitiga adalah sama dengan 1 dan kategori bernilai x dan y, kemudian:

dosa θ = y

cos θ = x

Rajah 2. Segitiga yang betul dalam lingkaran unit. Sumber: Wikimedia Commons.

Dengan cara ini, fungsi sinus dan kosinus sentiasa memperoleh nilai antara -1 dan 1, sementara yang lain:

tg θ = y/x

bahaya θ = 1/y

Sec θ = 1/x

Mereka tidak ditakrifkan ketika x Sama ada dan Mereka bernilai 0.

[TOC]

Fungsi trigonometri dalam pesawat Cartesian

Seperti yang akan kita lihat di bawah, fungsi trigonometri dicirikan dengan berkala. Oleh itu, mereka tidak bijektif, kecuali dalam domain terhad.

Fungsi f (x) = sin x

Bermula dalam bulatan trigonometri pada titik p (1.0), sudut adalah 0 radian. Kemudian jejari berputar dalam pengertian anti -horari dan fungsi sen x berkembang secara beransur -ansur sehingga mencapai π/2 radians (90º), bersamaan dengan 1.Kira -kira 571 radian.

Boleh melayani anda: Sudut Tambahan: Apa, Pengiraan, Contoh, Latihan

Di sana ia mencapai nilai y = 1 dan kemudian ia berkurangan sehingga ia mencapai sifar dalam radian π (180 °). Seterusnya ia berkurangan lebih banyak, kerana nilai menjadi negatif sehingga mencapai -1 apabila sudut adalah 3π/2 radian (270 °).

Akhirnya, ia meningkat lagi sehingga ia kembali ke sifar pada 360 °, di mana semuanya bermula lagi. Ini menjadikan y = sin x a fungsi berkala tempoh 2π, jadi fungsi sinus tidak bijective.

Di samping itu, grafik adalah simetri berkenaan dengan titik (0.0), oleh itu fungsi itu ganjil.

Kemudian graf y = sen x:

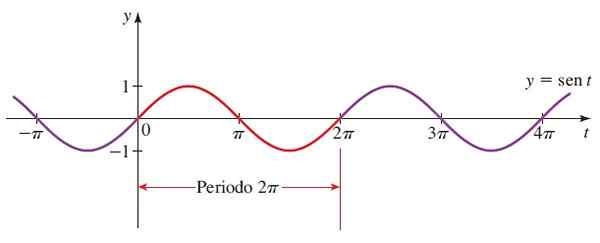Rajah 3. Fungsi graf f (x) = sin x. Sumber: Stewart, J. Preccculment: Matematik untuk Universiti.

Bahagian merah adalah tempoh pertama. Sudut negatif juga dipertimbangkan, kerana jejari bulatan trigonometri dapat berputar dalam jadual.

Sen x domain = Semua reales.

Julat atau laluan Sen X = [-1,1]

Fungsi f (x) = cos x

Pada titik p (1.0) fungsi coseno bernilai 1 dan dari sana berkurangan, mencapai 0 apabila sudut adalah π/2. Terus berkurangan dan mengambil nilai negatif, sehingga mencapai -1 pada sudut π.

Kemudian ia mula meningkat secara beransur -ansur sehingga mencapai 0 dalam 3π/2 dan mengambil nilai lagi apabila jejari telah berubah sepenuhnya. Dari situ kitaran diulang, kerana cos x berkala dan juga tork (simetri di sekitar paksi menegak).

Bentuk fungsi kosinus adalah sama dengan fungsi sinus, kecuali jika mereka dipindahkan π/2 satu berkenaan dengan yang lain.

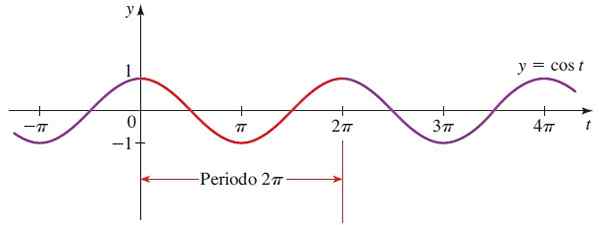Rajah 4. Fungsi graf f (x) = sin x. Sumber: Stewart, J. Preccculment: Matematik untuk Universiti.

Domain cos x = Semua reales.

Boleh melayani anda: anggaran tepat waktu

Julat atau laluan cos x = [-1,1]

Fungsi trigonometri yang tidak berterusan

Fungsi TG X, CTG X, SEC X dan HARS. Kerana ini bernilai 0 pada beberapa sudut, ketika mereka muncul dalam penyebut mereka membuat fungsi tidak berterusan.

Dan kerana sinus dan kosinus adalah fungsi berkala, fungsi tg x, ctg x, sec x, bahaya x juga.

Fungsi tangen f (x) = tg x

Untuk fungsi tangen, nilai ketidakpastian adalah: ± π/2, ± 3π/2, ± 5π/2 ... ada fungsi yang memerlukan nilai yang sangat besar atau sangat kecil. Secara umum ini berlaku untuk semua gandaan π bentuk (2n+1) π/2, baik positif dan negatif, dengan n = 0, 1, 2 ..

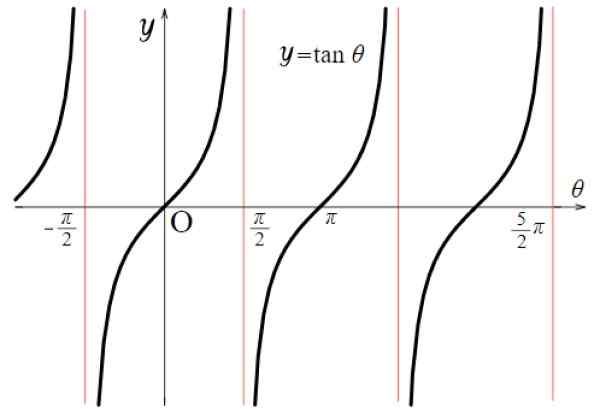Rajah 5. Fungsi graf f (x) = tg x. Sumber: Wikimedia Commons.

Oleh itu:

TG X Domain: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Tour Rank atau TG X: Semua reales.

Perhatikan bahawa fungsi f (x) = tg x diulang antara - π/2 dan + π/2, oleh itu tempohnya π. Di samping itu, simetri berkenaan dengan asal.

Fungsi cotangent f (x) = ctg x

Untuk fungsi ini, nilai ketidakpastian berlaku dalam 0, ± π, ± 2π ..., iaitu, keseluruhan gandaan π.

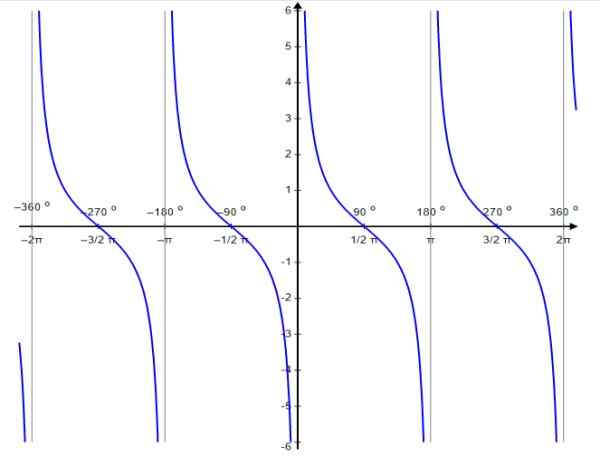Rajah 6. Fungsi graf f (x) = cotg x. Sumber: Wikimedia Commons.

Seperti fungsi tangen, fungsi cotangent adalah tempoh berkala π. Baginya ia dipenuhi bahawa:

Domain ctg x: D = x ∈ R / x ≠ n π; n ∈ Z

Julat atau laluan CTG X: Semua reales.

Fungsi pengeringan f (x) = sec x

Fungsi Sec X mempunyai titik ketidakselarasan dalam ± π/2, ± 3π/2, ± 5π/2 ..., di mana cos x = 0. Ia juga tempoh berkala π dan juga diperhatikan grafik bahawa fungsi tidak pernah mengambil nilai dalam selang (-1,1)

Boleh melayani anda: keseluruhan nombor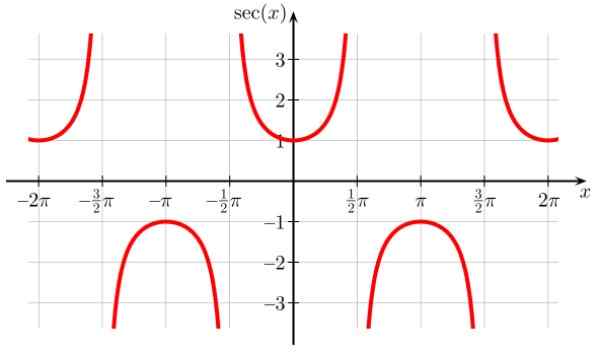 Rajah 7. Fungsi graf f (x) = sec x. Sumber: Wikimedia Commons.

DOMA SEC x: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Julat atau laluan sec x: Semua reais kecuali (-1,1)

Fungsi penuaian f (x) = bahaya x

Ia sama dengan fungsi pengeringan, walaupun ia dipindahkan ke kanan, oleh itu titik -titik ketidakselarasan adalah 0, ± π, ± 2π dan semua gandaan keseluruhan π. Ia juga berkala.

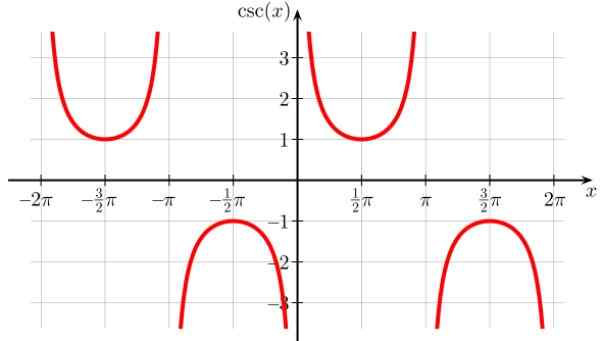Rajah 8. Fungsi graf f (x) = bahaya x. Sumber: Wikimedia Commons. Geek3/cc by-sa (https: // creativeCommons.Org/lesen/by-sa/4.0)

Domain bahaya x: D = x ∈ R / x ≠ n π; n ∈ Z

Laluan julat atau harmoni: Semua reais kecuali (-1,1)

Latihan diselesaikan

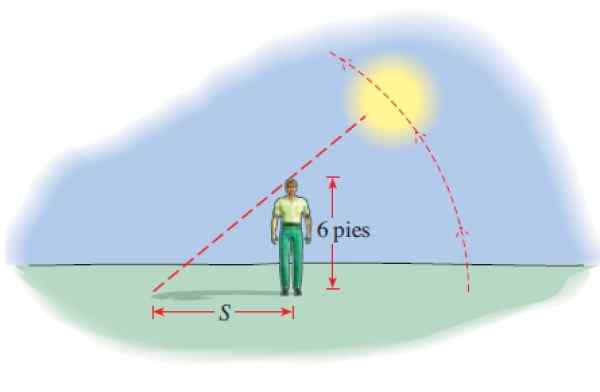
Seorang lelaki tinggi 6 -kaki memproyeksikan naungan yang panjangnya diberikan oleh:

S (t) = 6 │cot (π.T/12) │

Dengan s kaki dan t bilangan jam selepas pukul 6 pagi. Berapa bayangan pada pukul 8 pagi, jam 12 m, jam 2 petang dan jam 5:45 petang?

Penyelesaian

Kita mesti menilai fungsi untuk setiap nilai yang diberikan, ambil perhatian bahawa nilai mutlak mesti diambil, kerana panjang bayangan adalah positif:

-Pada pukul 8 pagi, 2 jam telah berlalu dari pukul 6 pagi, oleh itu t = 2 dan s (t) adalah:

S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π/6) │pies = 10.39 kaki.

-Apabila ia 12 n, t = 6 jam telah berlalu, oleh itu:

S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π/2) │pies = 0 kaki. (Pada masa itu matahari jatuh secara menegak di kepala orang itu).

-Pada pukul 2 petang mereka menghabiskan t = 8 jam:

S (8) = 6 │cot (π.8/12) │pies = 6 │cot (2π /3) │pies = 3.46 kaki.

-Ketika jam 5:45 petang, 11 telah berlalu 11.75 jam dari pukul 6 pagi, kemudian:

S (11.75) = 6 │cot (π x 11.75/12) │pies = 91.54 kaki. Pada masa ini bayang -bayang semakin lama.

Bolehkah pembaca mengira masa ketika bayangan orang itu sama dengan ketinggian mereka?

Rujukan

1. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
2. Figuera, j. 1999. Matematik. 1st. Dipelbagaikan. Edisi Bolivarian Collegiate.
3. Hoffman, J. Pemilihan masalah matematik. Jilid 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.