Geometri Analitik

Kami menerangkan apa geometri analisis, sejarahnya, kajian dan aplikasi apa

Apakah geometri analisis?

The Geometri Analitik Ia adalah cabang matematik di mana geometri dan algebra digabungkan, untuk menyelesaikan pelbagai masalah geometri melalui teknik algebra.

Gunakan sistem koordinat, seperti sistem koordinat Cartesian, yang berhutang namanya René Descartes. Dengan cara ini, adalah mungkin untuk mengaitkan lengkung dalam pesawat dan di angkasa, dengan persamaan algebra.

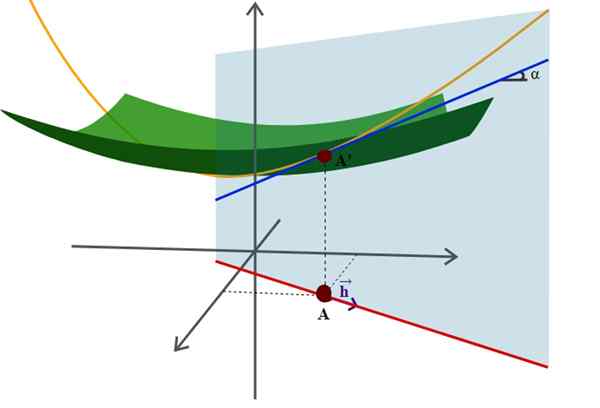
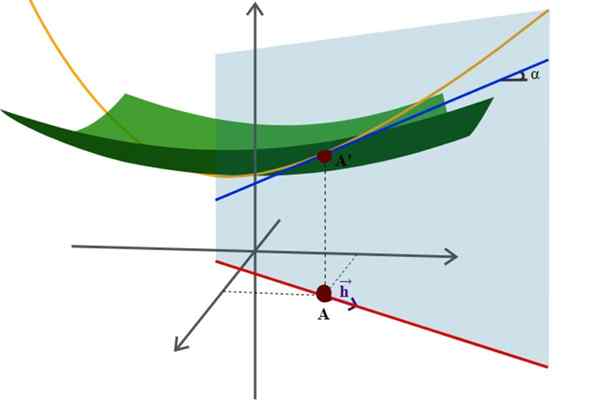Rajah permukaan di ruang angkasa dan derivatif arahnya, salah satu aplikasi geometri analisis yang lebih maju. Sumber: Wikimedia Commons.

Contohnya adalah persamaan yang terkenal dari radius r -riortion yang berpusat pada asal -usul sistem koordinat:

Tidak dinafikan, dalam banyak kes, lebih mudah untuk bekerja dengan ekspresi algebra dari lengkung, daripada dengan perwakilan geometri itu sendiri. Ini berlaku apabila mengira persimpangan antara lengkung, atau mencari garis tangen atau pengeringan kepada mereka.

Begitu juga, melalui geometri analisis, adalah mungkin untuk grafik fungsi susun atur. Dan seperti yang diketahui, fungsi membolehkan pemodelan masalah sains dan kejuruteraan. Oleh itu, geometri analisis hadir dalam kurikulum kerjaya yang berkaitan dengan bidang pengetahuan ini.

Sejarah Singkat Geometri Analisis

Geometri analisis berasal dari separuh pertama abad ke-17, dengan tangan dua ahli matematik Perancis yang terkenal: René Descartes (1596-1650) dan Pierre de Fermat (1601-1665).

Rene Descartes

Walau bagaimanapun, boleh dikatakan bahawa latar belakangnya berabad-abad lamanya, kepada ahli matematik Yunani Apollonius Pergamo (262-190 a.C.). Dia menulis risalah mengenai Conics, yang mana dia memberikan nama mereka: lilitan, elips, perumpamaan dan hiperbola.

Ia boleh melayani anda: Kompaun berkadar: Penjelasan, tiga peraturan kompaun, latihan

Oleh itu, kerja Apollonio adalah asas untuk, lebih lama kemudian, René Descartes Perancis dan Pierre de Fermat meletakkan asas -asas geometri analisis, secara bebas. Tetapi Descartes dianggap sebagai bapa sains ini, kerana dia adalah yang pertama untuk menerbitkan karya -karyanya.

Descartes, Fermat dan Euler

Dalam ucapan kaedah 1637, Descartes menyatukan dua disiplin yang sehingga itu telah dipisahkan: algebra dan geometri. Dalam karyanya, Descartes memperkenalkan sistem koordinat Cartesian, untuk mencari mata dalam pesawat dan di angkasa.

Ia juga menggunakan persamaan algebra kedua -dua pembolehubah, untuk menggambarkan bahagian kerucut dan didedikasikan untuk menyelesaikan masalah geometri dengan mereka. Juga untuk mewujudkan bahagian yang baik dari notasi matematik yang kini digunakan.

Pierre de Fermat lebih dikaitkan dengan optik daripada dengan geometri analisis, bagaimanapun, sumbangan mereka adalah ketara.

Pada tahun 1629, Fermat menyambung semula Conics of Apollonius Pergamo dan mencipta teknik -teknik yang membentuk geometri analisis, mencipta sistem koordinatnya sendiri dan dengan jelas menentukan konsep utama Tempat Geometri, yang mana kajian geometri analisis bermula.

Walau bagaimanapun, karya Fermat tidak melihat cahaya sehingga 1679, yang diterbitkan oleh anaknya, ketika ahli matematik sudah mati. Atas sebab ini, bapa geometri analisis dikaitkan dengan Descartes.

Selanjutnya kepada ahli matematik Perancis, Swiss Leonardo Euler (1707-1783) menubuhkan pangkalan formal geometri analisis. Euler memperkenalkan beberapa sistem koordinat dalam satah dan ruang: koordinat segi empat tepat, kutub dan serong, serta transformasi dari satu sistem ke sistem lain.

Boleh melayani anda: Bagaimana maklumat yang diperolehi dalam tinjauan?

Dalam karya -karyanya mengenai geometri analisis, Euler juga memperdalam klasifikasi pelbagai lengkung, menurut tahap persamaan algebra wakil (perintah ketiga dan keempat) dan mengkaji sifatnya secara intensif, persamaan tangen, kelengkungan, simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak simetri dan banyak lebih.

Apa Kajian Geometri Analitik?

Secara umum, geometri analisis memberi tumpuan kepada kajian unsur -unsur geometri, seperti titik, segmen, garisan, lengkung, permukaan dan jumlah. Untuk melakukan ini, seperti yang dinyatakan di atas, ia menetapkan persamaan algebra yang menggambarkan dan mengaitkan unsur -unsur ini, yang membolehkan pengurusan mereka melalui teknik algebra.

Objektif utama geometri analisis, dengan cara yang sangat ringkasan, adalah berikut:

1. Menetapkan sistem koordinat Cartesian dan sistem koordinat kutub, untuk mencari mata dalam pesawat, serta lanjutannya ke titik di ruang angkasa.
2. Lukis segmen, lurus, lengkung dan permukaan pada pesawat dan ruang Cartesian.
3. Menyimpulkan persamaan yang secara analitik menggambarkan lengkung dan pembinaannya di atas kapal terbang dan/atau ruang, serta kajian semua sifatnya.
4. Mengklasifikasikan lengkung, permukaan dan jilid.
5. Memperoleh formula asas untuk menyelesaikan masalah pada titik yang ketara, lurus, rancangan, sudut, paralelisme, keseragaman, jarak, persimpangan, kawasan dan banyak lagi.
6. Selesaikan masalah geometri melalui penggunaan kaedah algebra, yang mana formula merujuk kepada titik -titik yang ketara, persamaan untuk garis, rancangan, sudut, jarak antara titik, antara garis dan titik, titik tangensi, garis kering, kawasan, kawasan dan banyak lagi.
7. Bekerja dengan ruang vektor dan produk antara vektor.

Jarak antara dua mata

Sebagai contoh banyak aplikasi geometri analisis, salah satu yang paling mudah ialah pengiraan jarak antara dua titik pesawat. Adalah dua mata p₁ Dan p₂, koordinat (x₁,dan₁) dan (x₂,dan₂) masing -masing, jarak d di antara mereka dikira oleh:

Boleh melayani anda: trinomial

Koordinat kutub

Titik pesawat boleh ditentukan melalui jarak "R" ke asal sistem koordinat, yang dipanggil polo, dan sudut yang membentuk garis yang mengandungi titik dan tiang, dengan paksi mendatar atau paksi kutub.

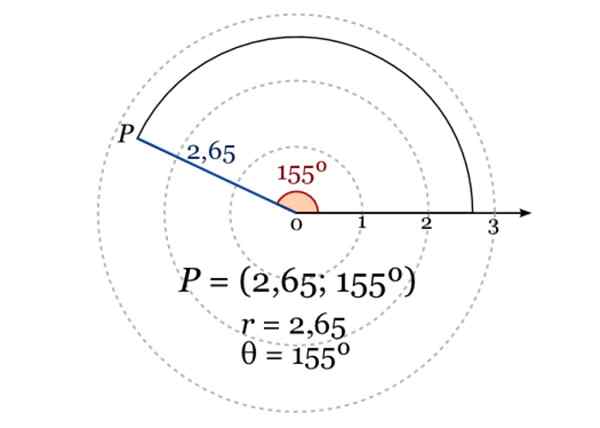Imej menunjukkan koordinat kutub titik p, di mana r = 2.65 dan sudut dalam darjah berkenaan dengan paksi kutub ialah 155º. Sumber: Wikimedia Commons.

Aplikasi geometri analisis

Asas Pengiraan Infinitesimal

Geometri analisis adalah penting untuk pembangunan pengiraan yang kecil, kerana ia memudahkan perwakilan grafik lengkung dan fungsi, dan bekerja dengan mereka dengan cara analisis, untuk mewujudkan model yang mewakili fenomena alam.

Peta

Sistem koordinat Cartesian membantu membuat peta dan mengenal pasti tempat melalui latitud dan panjang, bersamaan dengan koordinat Cartesian titik dalam satah.

Pengiraan topografi

Jenis sistem koordinat yang berbeza digunakan dalam topografi dan merupakan asas kajian dan aplikasi mereka. Antaranya ialah sistem koordinat kutub yang diterangkan di atas.

Trajektori badan langit

Bahagian kerucut, yang diterangkan melalui geometri analisis, mengambil bahagian dalam fenomena alam yang penting, seperti trajektori badan langit, tertakluk kepada kekuatan graviti. Sebagai contoh, planet dan beberapa komet menggambarkan trajektori elips di sekitar matahari, dengan ini terletak di salah satu lampu sorot.

Senibina dan pembinaan awam

Banyak lengkung adalah sebahagian daripada pembinaan seni bina, sebagai contoh, kabel jambatan gantung boleh mengambil bentuk perumpamaan.

Sistem kedudukan global

Sistem kedudukan atau GPS global menjadikan lokasi yang mungkin dengan ketepatan, serta objek bergerak, seperti kenderaan dan bot. Ia juga membantu orang mendapatkan lebih mudah ke destinasi mereka, membimbing mereka di laluan terbaik.