Gravicentro

Apakah Cukai?

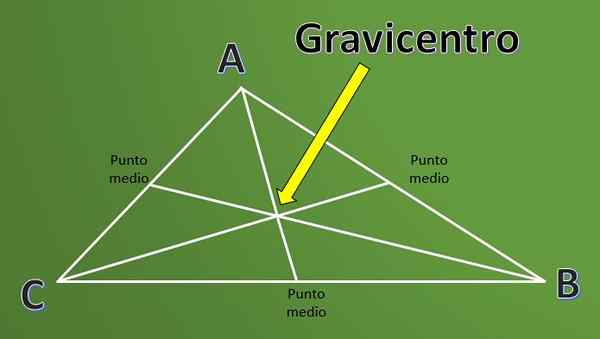
Dia Gravicentro Ini adalah definisi yang digunakan secara meluas dalam geometri ketika bekerja dengan segitiga. Untuk memahami definisi gravicentro, pertama kali perlu mengetahui definisi "sederhana" segitiga.

Medians segitiga adalah segmen garis yang bermula di setiap puncak dan mencapai titik tengah dari seberang untuk mengatakan puncak.

Titik persimpangan tiga median segitiga dipanggil Baricentro atau juga dikenali sebagai cukai. Tidak cukup hanya untuk mengetahui definisi, sangat menarik untuk mengetahui bagaimana perkara ini dikira.

Pengiraan Balicenter

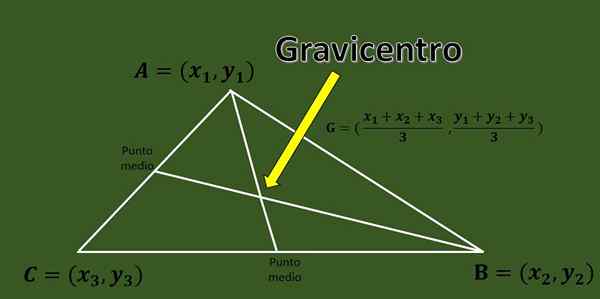
Memandangkan segitiga ABC dengan simpang a = (x1, y1), b = (x2, y2) dan c = (x3, y3), gravicentro adalah persimpangan tiga median segitiga.

Formula pesat yang membolehkan pengiraan cukai segitiga, koordinat simpang yang diketahui adalah:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

Dengan formula ini, anda dapat mengetahui lokasi Gravicentro dalam pesawat Cartesian.

Ciri -ciri Cukai

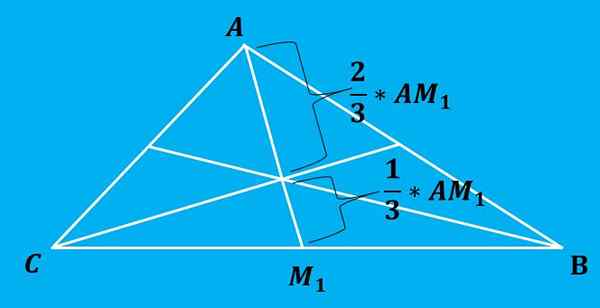
Tidak perlu mengesan tiga median segitiga, kerana ketika menggambar dua daripadanya, ia akan dibuktikan di mana percukaian itu.

Percukaian membahagikan setiap median ke dalam 2 bahagian yang perkadarannya ialah 2: 1, iaitu, kedua -dua segmen setiap median dibahagikan kepada segmen panjang 2/3 dan 1/3 dari jumlah panjang, jarak yang lebih besar adalah yang ada Apa yang ada di antara puncak dan risalah.

Imej berikut menggambarkan harta ini lebih baik.

Formula untuk pengiraan cukai sangat mudah untuk digunakan. Cara untuk mendapatkan formula ini adalah dengan mengira persamaan lurus yang setiap median mentakrifkan dan kemudian mencari titik pemotongan garis -garis ini.

Latihan

Berikut adalah senarai kecil masalah mengenai pengiraan Balicenter.

1.- Memandangkan segitiga simpang a = (0.0), b = (1.0) dan c = (1,1), hitung percukaian segitiga tersebut.

Menggunakan formula yang diberikan, dapat dengan cepat menyimpulkan bahawa gravicentro segitiga ABC adalah:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Sekiranya segitiga mempunyai simpul a = (0.0), b = (1.0) dan c = (1/2.1), apakah koordinat cukai?

Oleh kerana simpang segitiga diketahui, formula untuk pengiraan cukai digunakan. Oleh itu, Gravicentro mempunyai koordinat:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Kirakan pembayar cukai yang mungkin untuk segitiga sama rata supaya dua simpangnya adalah A = (0.0) dan B = (2.0).

Dalam latihan ini, hanya dua simpang segitiga yang ditentukan. Untuk mencari gravicenters yang mungkin, puncak ketiga segitiga mesti dikira terlebih dahulu.

Oleh kerana segitiga adalah sama dan jarak antara a dan b ialah 2, puncak ketiga c mestilah berada pada jarak 2 a dan b.

Menggunakan hakikat bahawa dalam segitiga sama rata ketinggian bertepatan dengan median dan juga menggunakan teorem Pythagoras, dapat disimpulkan bahawa pilihan untuk koordinat puncak ketiga adalah c1 = (1, √3) atau c2 = (1, - - - √3).

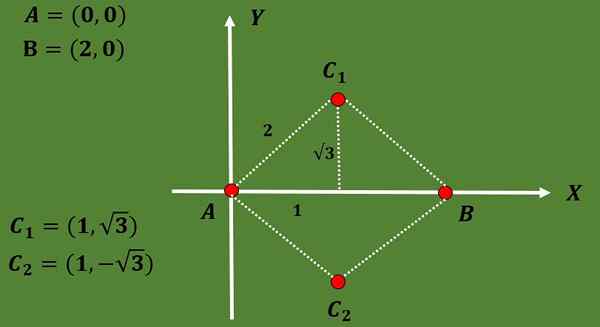
Supaya koordinat dua gravicenters yang mungkin adalah:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -√3)/3) = (3/3, -√3/3) = (1, -√3/3).

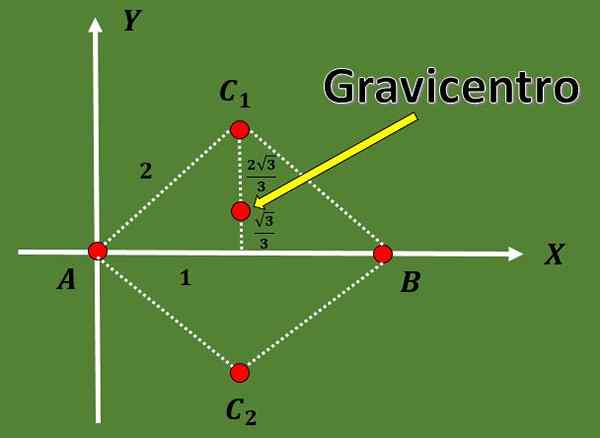
Terima kasih kepada akaun sebelumnya, juga dapat diperhatikan bahawa median dibahagikan kepada dua bahagian yang perkadarannya adalah 2: 1.