Icosagono

Apa itu icogon?

A Icosagono atau isodecagon Ia adalah poligon yang mempunyai 20 sisi. Poligon adalah angka rata yang dibentuk oleh urutan segmen garis terhingga (lebih daripada dua), yang melampirkan kawasan satah.

Setiap segmen baris dipanggil sisi dan persimpangan setiap pasangan sisi dipanggil puncak. Menurut bilangan pihak, poligon menerima nama tertentu.

Yang paling biasa adalah segitiga, kuadrilateral, pentagon dan segi enam, yang masing -masing mempunyai 3, 4, 5 dan 6, tetapi boleh dibina dengan bilangan sisi yang dikehendaki.

Ciri -ciri icogon

Berikut adalah beberapa ciri poligon dan aplikasi mereka dalam icogon.

1- Klasifikasi

Icosgono, sebagai poligon, boleh diklasifikasikan sebagai biasa dan tidak teratur, di mana perkataan biasa merujuk kepada fakta bahawa semua pihak mempunyai panjang yang sama dan sudut dalaman mengukur semua yang sama; Jika tidak dikatakan bahawa icosagon (poligon) tidak teratur.

2- isodecagon

Icosgon biasa juga dipanggil isodogon biasa, kerana untuk mendapatkan icosgon biasa -gauge apa yang perlu dilakukan adalah bisecar (membahagikan kepada dua bahagian yang sama) setiap sisi decagon biasa (10 sisi poligon).

3- perimeter

Untuk mengira perimeter "P" poligon biasa, bilangan sisi didarabkan dengan panjang setiap sisi.

Dalam kes tertentu icogon, perimeter adalah sama dengan 20xl, di mana "l" adalah panjang setiap sisi.

Sebagai contoh, jika anda mempunyai icosagon sampingan 3 cm biasa, perimeternya sama dengan 20x3cm = 60 cm.

Jelas bahawa, jika isocagon tidak teratur, formula sebelumnya tidak dapat digunakan.

Dalam kes itu, 20 pihak mesti ditambah secara berasingan untuk mendapatkan perimeter, iaitu, perimeter "P" adalah sama dengan Σli, dengan i = 1.2, ..., 20.

4- Diagonal

Bilangan pepenjuru "d" yang mempunyai poligon adalah sama dengan n (n-3)/2, di mana n mewakili bilangan sisi.

Dalam kes icogon, ia mesti d = 20x (17)/2 = 170 pepenjuru.

5- Jumlah sudut dalaman

Terdapat formula yang membantu mengira jumlah sudut dalaman poligon biasa, yang boleh digunakan untuk icosgon biasa.

Formula terdiri daripada pengurangan 2 kepada bilangan sisi poligon dan kemudian mengalikan nombor ini sebanyak 180º.

Cara formula ini diperolehi ialah kita dapat membahagikan poligon sisi N ke dalam segitiga N-2, dan menggunakan fakta bahawa jumlah sudut dalaman segitiga adalah 180º Formula diperolehi.

Dalam imej berikut, formula untuk enegon biasa (poligon 9 -sisi) digambarkan.

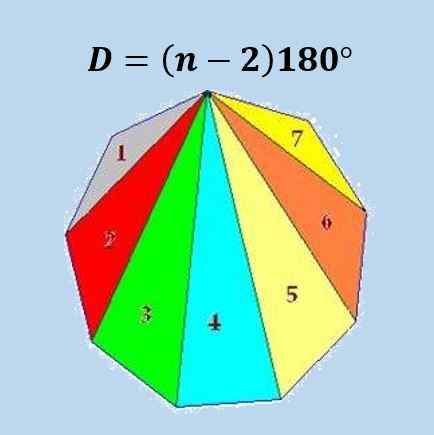
Menggunakan formula anterior, diperolehi bahawa jumlah sudut dalaman mana -mana icosagon adalah 18 × 180º = 3240º atau 18π.

6- kawasan

Untuk mengira kawasan poligon biasa, sangat berguna untuk mengetahui konsep apothem. Apotheme adalah garis tegak lurus yang pergi dari pusat poligon biasa ke titik tengah mana -mana sisinya.

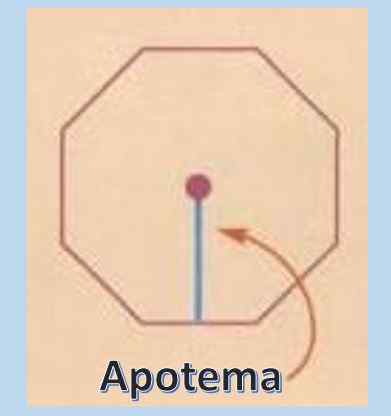
Sebaik sahaja panjang apothem diketahui, kawasan poligon biasa adalah a = pxa/2, di mana "p" mewakili perimeter dan "a" apotheme.

Dalam kes icosagon biasa, anda ada di kawasan anda ialah A = 20xlxa/2 = 10xlxa, di mana "L" adalah panjang setiap sisi dan "a" apothemnya.

Sebaliknya, jika anda mempunyai poligon yang tidak teratur dari sisi N, untuk mengira kawasannya, poligon dibahagikan kepada segitiga N-2 yang diketahui, maka kawasan setiap segitiga N-2 ini dikira dan akhirnya semua ini ditambah kawasan.

Kaedah yang diterangkan di atas dikenali sebagai triangulasi poligon.

Rujukan

1. Unsur Geometri: Dengan banyak latihan dan geometri kompas. Universiti Medellin.
2. Iger. (s.F.). Matematik semester pertama Tacaná. Iger.