Demonstrasi identiti Pythagorean, contoh, latihan

Adalah Identiti Pythagorean Semua persamaan trigonometri yang dipenuhi untuk sebarang nilai sudut dan berdasarkan teorem Pythagoras. Identiti Pythagorean yang paling terkenal adalah identiti trigonometri asas:

Sen²(α) + cos²(α) = 1

Rajah 1. Identiti trigonometri Pythagorean.

Ia masih penting dan menggunakan identiti Pythagorean Tangen dan Secant:

Jadi²(α) + 1 = sec²(α)

Dan identiti trigonometri Pythagorean yang melibatkan cotangent dan penuai:

1 + ctg²(α) = CSC²(α)

[TOC]

Demonstrasi

Sebab -sebab trigonometri payudara dan Cosine Mereka diwakili dalam lilitan radius satu (1) yang dikenali sebagai bulatan trigonometri. Bulatan ini mempunyai pusat pada asal koordinat atau.

Sudut diukur dari separuh -axis positif x, contohnya sudut α dalam Rajah 2 (lihat kemudian). Bertentangan dengan tangan jam jika sudut positif, dan ke arah tangan jika ia adalah sudut negatif.

Semi -right dengan asal atau dan sudut α ditarik, yang memintas lingkaran unit pada titik p. Point P diunjurkan secara ortogonal pada paksi mendatar x yang menimbulkan titik c. Begitu juga P diunjurkan secara serentak pada paksi menegak dan menimbulkan titik s.

Anda mempunyai segitiga OCP yang betul di c. 

Payudara dan kosinus

Harus diingat bahawa alasan trigonometri payudara Ia ditakrifkan pada segitiga yang betul seperti berikut:

Bosom sudut segitiga adalah nisbah atau nisbah antara Cateto yang menentang sudut dan hipotenus segitiga.

Digunakan untuk segi tiga OCP Rajah 2 akan seperti ini:

Dosa (α) = cp / op

Tetapi CP = OS dan OP = 1, jadi:

Dosa (α) = os

Yang bermaksud bahawa unjuran pada paksi y mempunyai nilai yang sama dengan pangkuan sudut yang ditunjukkan. Harus diingat bahawa nilai maksimum payudara sudut (+1) berlaku apabila α = 90º dan minimum (-1) apabila α = -90º atau α = 270º.

Boleh melayani anda: ruang vektor: asas dan dimensi, aksioma, sifat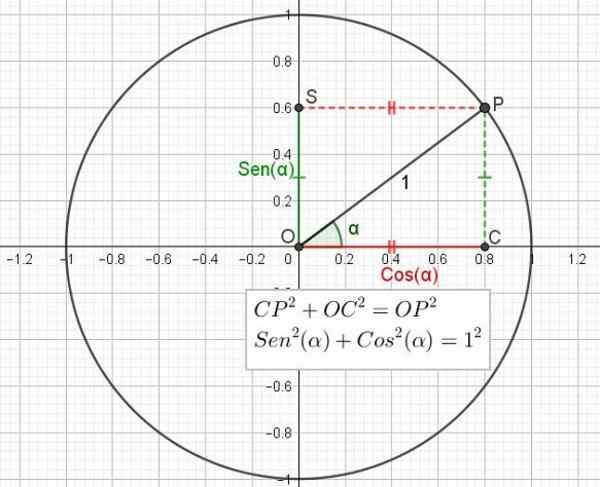Rajah 2. Lingkaran Trigonometrik menunjukkan hubungan antara teorem Pythagoras dan identiti trigonometri asas. (Huraian sendiri)

Begitu juga, kosinus sudut adalah nisbah antara kategori bersebelahan dengan sudut dan hipotenus segitiga.

Digunakan untuk segi tiga OCP Rajah 2 akan seperti ini:

Cos (α) = oc / op

Tetapi OP = 1, jadi:

Cos (α) = oc

Yang bermaksud bahawa unjuran OC pada paksi x mempunyai nilai yang sama dengan pangkuan sudut yang ditunjukkan. Harus diingat bahawa nilai maksimum kosinus (+1) berlaku apabila α = 0º atau α = 360º, manakala nilai minimum kosinus adalah (-1) apabila α = 180º.

Identiti asas

Untuk segi tiga segi empat tepat OCP, teorem Pythagoras digunakan, yang menyatakan bahawa jumlah persegi kategori adalah sama dengan kuadrat hipotenus:

Cp² + OC² = Op²

Tetapi telah dikatakan bahawa cp = os = sin (α), bahawa oc = cos (α) dan bahawa op = 1, jadi ungkapan sebelumnya dapat ditulis semula bergantung pada sinus dan kosinus sudut:

Sen²(α) + cos²(α) = 1

Paksi tangen

Sama seperti paksi x dalam bulatan trigonometri adalah paksi kosinus dan paksi dan paksi payudara, dengan cara yang sama terdapat paksi tangen (lihat Rajah 3) yang tepatnya tangen garis ke unit bulatan pada titik pada koordinat titik b (1, 0). 

Sekiranya anda ingin mengetahui nilai tangen sudut, sudutnya diambil dari separuh -axle positif x, persimpangan sudut dengan paksi tangen mentakrifkan titik q, panjang segmen OQ adalah tangen sudut.

Boleh melayani anda: derivatif algebra

Ini kerana dengan definisi, tangen sudut α adalah Cateto QB yang bertentangan antara OB Cateto bersebelahan. Iaitu SO (α) = qb / ob = qb / 1 = qb.

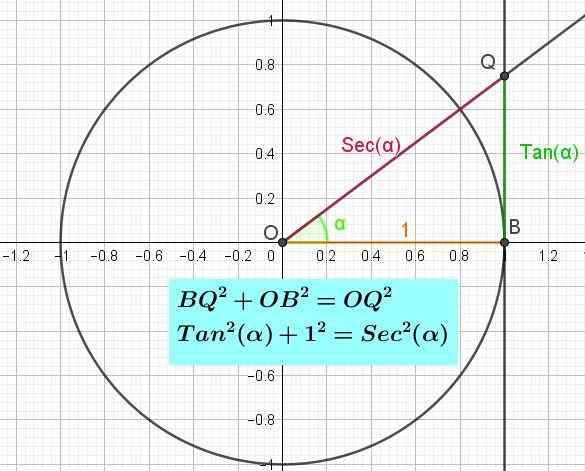Rajah 3. Bulatan trigonometri yang menunjukkan paksi tangen dan identiti pythagorean tangen. (Huraian sendiri)

Identiti pythagorean tangen

Identiti Pythagorean tangen dapat ditunjukkan jika segitiga segi empat tepat di B (Rajah 3) dipertimbangkan (Rajah 3). Memohon teorem pythagoras untuk tersebut² + Ob² = OQ². Tetapi telah dikatakan bahawa bq = tan (α), bahawa OB = 1 dan bahawa OQ = sec (α), sehingga menggantikan kesamaan pythagoras untuk segitiga kanan OBQ ia mempunyai:

Jadi²(α) + 1 = sec²(α).

Contoh

Sahkan sama ada atau tidak identiti Pythagorean dipenuhi dalam segi empat tepat segi empat tepat Catetos AB = 4 dan BC = 3.

Penyelesaian: Kategori diketahui, perlu menentukan hipotenus, iaitu:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Sudut ∡bac akan dipanggil α, ∡bac = α. Sekarang alasan trigonometri ditentukan:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = bc / ab = 3/4 

Cotan α = AB / BC = 4/3 

SEC α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Ia bermula dengan identiti trigonometri asas:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Disimpulkan bahawa ia dipenuhi.

- Identiti Pythagorean seterusnya adalah tangen:

Jadi²(α) + 1 = sec²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

Dan disimpulkan bahawa identiti tangen itu disahkan.

- Begitu juga dengan Cotangent:

Boleh melayani anda: pilihan rawak dengan atau tanpa penggantian

1 + ctg²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Disimpulkan bahawa ia juga dipenuhi, yang telah menyelesaikan tugas mengesahkan identiti Pythagorean untuk segitiga yang diberikan.

Latihan yang diselesaikan

Uji identiti berikut, berdasarkan definisi sebab trigonometri dan identiti pytagoric.

Latihan 1

Buktikan apa cos² x = (1 + sen x) (1 - sin x).

Penyelesaian: Ahli yang betul mengiktiraf produk yang ketara dari pendaraban binomial oleh konjugasi yang, seperti yang diketahui, adalah perbezaan dataran:

Cos² x = 1² - Sen² x

Kemudian istilah dengan payudara di sebelah kanan pas ke sebelah kiri dengan tanda yang diubah:

Cos² X + sen² x = 1

Mengetahui bahawa identiti trigonometri asas telah dicapai, jadi disimpulkan bahawa ungkapan yang diberikan adalah identiti, iaitu, ia dipenuhi untuk sebarang nilai x.

Latihan 2

Bermula dari identiti trigonometri asas dan menggunakan definisi alasan trigonometri untuk menunjukkan identiti Pythagorean penuai.

Penyelesaian: Identiti asas ialah:

Sen²(x) + cos²(x) = 1

Kedua -dua ahli dibahagikan antara Sen²(x) dan penyebut diedarkan pada ahli pertama:

Sen²(x)/dosa²(x) + cos²(x)/dosa²(x) = 1/sen²(x)

Ia dipermudahkan:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) adalah identiti (non -pythagorean) yang disahkan oleh definisi alasan trigonometri. Dengan cara yang sama ia berlaku dengan identiti berikut: 1/sin (x) = csc (x).

Akhirnya anda mesti:

1 + ctg²(x) = CSC²(x)

Rujukan

1. Baldor J. (1973). Geometri rata dan ruang dengan pengenalan kepada trigonometri. Kebudayaan Amerika Tengah. C.Ke.
2. C. Dan. Ke. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Kumpulan Editorial Patria.
4. Iger. (s.F.). Matematik semester pertama Tacaná. Iger.
5. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
6. Miller, Heeren, & Hornsby. (2006). Matematik: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
7. Patiño, m. (2006). Matematik 5. Progreso editorial.
8. Wikipedia. Identiti dan formula trigonometri. Pulih dari: Adakah.Wikipedia.com