Sisi homolog

Kami menerangkan apa sisi homolog, dengan contoh dan latihan diselesaikan

Apa sisi homolog?

The sisi homolog Dalam dua angka geometri rata adalah yang saling bersesuaian, menjaga persamaan. Contohnya, tangan kanan seseorang homolog dengan tangan kanan orang lain.

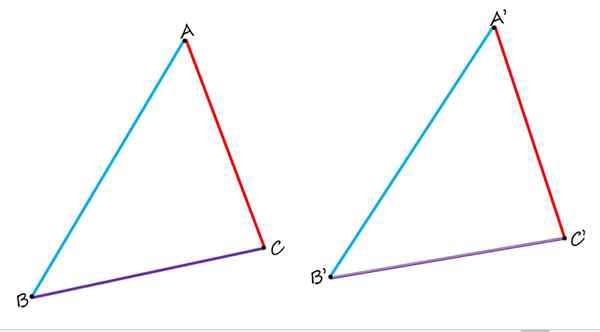
Dalam geometri rata, tidak hanya sisi homolog, tetapi simpang dan sudut homolog juga. Untuk melihatnya, pertimbangkan angka berikut, yang terdiri daripada dua segitiga yang sama ABC dan A'B'C ':

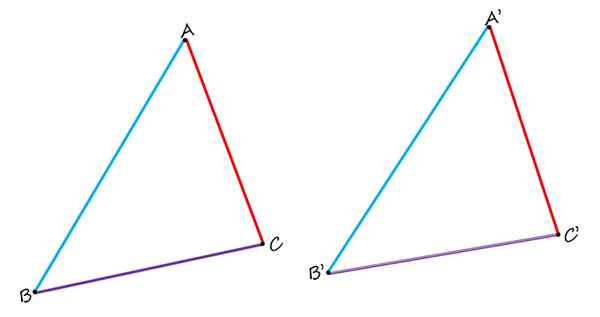Di dua segitiga yang sama ditunjukkan, ab dan a'b ', adalah homolog, serta sisi bc dan b'c' dan ac dan a'c '. Sumber: f. Zapata.

Apabila membandingkannya, jelas diperhatikan bahawa sisi ab dan a'b 'berwarna biru adalah homolog, kerana mereka menduduki kedudukan yang sama di setiap segitiga. Sisi bc dan b'c 'dalam ungu juga homologus. Dan akhirnya, sisi ac merah homolog ke sisi a'c '.

Penjelasan

Dari yang disebutkan di atas, ia mengikuti bahawa pihak homolog adalah mereka yang menduduki kedudukan relatif yang sama dalam angka dengan cara yang sama. Dalam imej terdahulu, dua segitiga yang sama digunakan untuk menunjukkan idea itu, tetapi ini dapat dengan mudah menyamar sebagai angka geometri rata yang lain, yang dibentuk oleh sisi berturut -turut yang ditutup.

Angka -angka ini dipanggil poligon. Sebagai contoh, segitiga dan kuadrilateral masing -masing adalah poligon dari 3 dan 4 sisi.

Konsep sisi homolog adalah penting kerana ia membolehkan untuk menentukan kriteria persamaan antara poligon, seperti yang akan dilihat tidak lama lagi. Angka -angka yang serupa mempunyai bentuk yang sama dan mengekalkan perkadaran yang sama di antara pihak mereka, walaupun mereka tidak sama saiznya.

Dan walaupun sejauh ini rujukan dibuat hanya kepada angka rata, terdapat juga angka serupa dalam tiga dimensi. Mereka mudah diperhatikan di rak pasar raya, apabila produk yang sama dijual dalam bekas yang sama, tetapi dengan saiz yang berbeza.

Boleh melayani anda: logik matematik

Kata -kata lain yang digunakan secara bergantian dalam geometri untuk merujuk kepada sisi homolog dalam angka geometri adalah: sisi yang sama, sisi masing -masing dan sisi yang setara.

Simpul dan sudut homolog

Seperti sisi, simpang homolog juga ditakrifkan, yang menyatukan pasangan homolog. Contohnya, simpang a dan 'dari angka sebelumnya adalah homolog. Begitu juga, pasangan simpang b dan b 'dan c dan c' adalah homolog.

Akhirnya, sudut homolog menduduki kedudukan relatif yang sama dalam angka. Tudung sudut homolog adalah homolog.

Untuk menggambarkan idea itu, ambil sudut antara sisi biru dan ungu segitiga kiri, yang boleh dilambangkan sebagai ∠ABC. Sudut ini mempunyai rakan sejawatannya di sudut ∠A'B'C ', dari segitiga ke kanan.

Bahagian sudut sudut ini adalah B, yang seperti yang ditunjukkan sebelumnya, adalah rakan sejawat dengan B ', dan dua pasang sudut homolog dari segitiga yang ditunjukkan adalah:

• ∠BCA dan ∠B'C'A '
• ∠CAB dan ∠C'A'B '

Persamaan poligon

Bagi mana -mana dua poligon yang sama, syarat -syarat berikut mesti dipenuhi:

• Semua pasang sudut homolog mempunyai ukuran yang sama
• Pasangan homolognya berkadar.

Kedua -dua syarat mesti dipenuhi secara serentak untuk memastikan persamaan. Ia segera diperhatikan mengapa.

Dalam angka berikut terdapat dua kuadrilaterals yang jelas tidak serupa. Ini disebabkan oleh fakta bahawa status pertama mingguan dipenuhi, tetapi yang kedua tidak:

Dua kuadrilaterals yang tidak serupa, walaupun sudut homolog mereka mempunyai ukuran yang sama. Sumber: f. Zapata.

Walaupun dalam angka pasangan mereka sudut homolog mempunyai ukuran yang sama, kerana semuanya adalah sudut lurus (mereka mengukur 90º), angka -angka tidak sama, kerana pasangan mereka tidak berkadar.

Boleh melayani anda: fungsi injective: apa yang terdiri daripada, apa itu dan contohnya

Sebaliknya, kedua -dua kuadrilaterals ini mempunyai sisi homolog dengan ukuran yang sama, tetapi sudut homolog tidak mengukur perkara yang sama. Oleh itu, angka jelas tidak serupa.

Dua kuadrilaterals dengan sisi homolog dengan ukuran yang sama, tetapi dengan sudut dalaman yang berbeza, oleh itu mereka bukan angka serupa. Sumber: f. Zapata.

Sebab persamaan

Sekiranya dua angka adalah serupa, kuota antara sisi homolog adalah sama dan dipanggil sebab persamaan.

Menandakan sisi salah satu tokoh seperti A, B, C, D ... dan yang sepadan dengan angka lain seperti A ', B', C ', D

Perimeter dan bidang angka serupa

Nisbah kesamaan membolehkan mendapatkan hubungan antara perimeter, kawasan dan jumlah dua angka serupa.

Alasan perimeter untuk dua angka serupa

Perimeter P poligon ditakrifkan sebagai jumlah semua sisinya. Jika anda mempunyai angka yang sisinya adalah ', b', c ', d' ..., perimeter p 'adalah:

P '= a' + b ' + c' + d '.. .

Sekiranya poligon lain sama dengan ini, dan sisinya adalah A, B, C, D ..., ia dipenuhi bahawa:

Dan oleh itu:

A = r ∙ a '

Anda boleh mengesahkan perkara yang sama untuk sisi lain dari angka ini. Jadi perimeter p dinyatakan sebagai:

P = a + b + c + d .. . = r ∙ ' + r ∙ b' + r ∙ c ' + r ∙ d' + ..

Oleh kerana "R" adalah faktor umum kepada semua penagih, hubungan antara p dan p 'adalah:

P = r ∙ p '

Ini bermaksud bahawa alasan perimeter antara dua poligon yang serupa adalah sama dengan alasan persamaan.

Sebab untuk dua angka serupa

Jika dua angka serupa masing -masing mempunyai kawasan A dan A ', ini berkaitan melalui:

Boleh melayani anda: Latihan pelepasan formula

A = r²∙ a '

Di mana "r" adalah sebab persamaan angka.

Nisbah kelantangan dua angka serupa

Mereka adalah dua angka tiga dimensi yang sama, masing -masing, masing -masing, V dan V '. Hubungan antara mereka, melalui "R" adalah:

V = r³∙ v '

Contoh

Cetak biru

Bahagian tanah, tumbuhan bangunan atau pakaian, pada skala yang lebih kecil di atas kertas boleh diwakili. Rancangan mempunyai kelebihan untuk dapat mengambilnya dan membuat pengubahsuaian yang berkaitan dengan mudah, sebelum dipraktikkan pada objek sebenar.

Peta

Mereka biasanya perwakilan dalam bidang tanah luas tanah, dari sebuah kampung ke benua. Mereka juga dibuat pada skala tertentu.

Mereka mempunyai banyak aplikasi dan terdapat banyak jenis. Sebagai contoh, melalui peta medan boleh diterangkan, dan apabila ia terletak pada titik tertentu, laluan terbaik untuk pergi dari titik ke yang lain ditentukan.

Model

Mereka adalah perwakilan tiga dimensi pada skala objek seperti kereta, bangunan dan pembinaan secara umum.

Latihan diselesaikan

Nilai berikut sesuai dengan sisi beberapa segitiga yang serupa. Cari sebab persamaan dan nilai "x" dan "y":

Segitiga 1: 5, 8, 10

Segitiga 2: 150, x, y

Penyelesaian

Sebab persamaan adalah kuota:

R = 150/5 = 30

Oleh itu:

x = 30 × 8 = 240

y = 10 × 30 = 300