Undang -undang Formula Lenz, Persamaan, Aplikasi, Contoh

The Undang -undang Lenz Ia menetapkan bahawa polaritas daya elektromotor yang disebabkan oleh litar tertutup, kerana variasi aliran medan magnet, sedemikian rupa sehingga ia menentang variasi aliran tersebut.

Tanda negatif yang dimasukkan ke dalam undang-undang Faraday, mengambil kira undang-undang Lenz, sebagai sebab mengapa ia dipanggil undang-undang Faraday-Lenz dan yang dinyatakan seperti berikut:

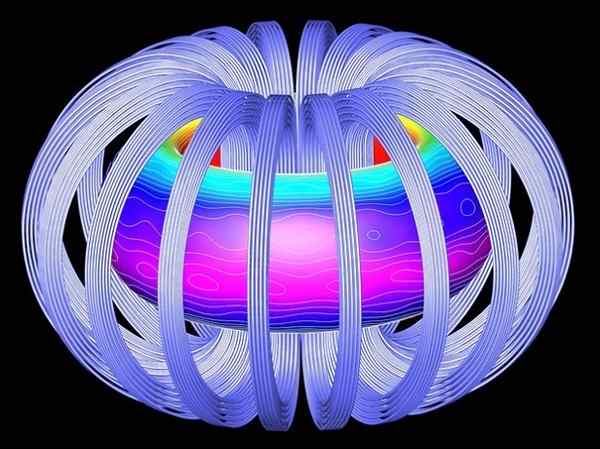
Rajah 1. Gegelung toroidal dapat mendorong arus di pemandu lain. Sumber: Pixabay.

[TOC]

Formula dan persamaan

ε mewakili daya elektromotor yang disebabkan, disingkat sebagai Fem, Φ Ia adalah aliran medan magnet dan t Sudah tiba masanya. Unit dalam sistem antarabangsa (SI) untuk Fem Mereka adalah volt (v).

Bagi bahagiannya aliran medan magnet Φ Ia ditakrifkan oleh produk skalar berikut:

Begitu banyak B sebagai n Mereka adalah magnitud vektor dan boleh dilambangkan dengan berani atau dengan anak panah pada surat itu. B Ia adalah vektor medan magnet dan n Ia adalah vektor unit (magnitud sama dengan 1) tegak lurus ke permukaan yang diseberang B.

Dalam persamaan yang ditunjukkan B Ia tetap dan unit untuk Φ Di SI untuk aliran medan magnet ialah Weber (W):

1 Weber = 1 Tesla. meter²

Cara lain untuk menyatakan Φ Ia adalah yang diperoleh dengan menggunakan definisi produk skalar:

Φ = b.Ke.cos θ

Dalam persamaan ini, B Ia adalah magnitud medan magnet (tanpa berani atau anak panah, untuk membezakan vektor dari magnitudnya), A adalah kawasan permukaan yang diseberang oleh medan dan θ adalah sudut antara vektor B dan n.

Aliran medan magnet boleh diubah dengan cara yang berbeza dari masa ke masa, untuk membuat a Fem disebabkan oleh gelung - litar tertutup - kawasan ke. Sebagai contoh:

-Menjadikan pembolehubah medan magnet dari masa ke masa: B = B (T), Menjaga kawasan dan sudut malar, kemudian:

-Kawasan spas boleh berbeza -beza, membiarkan magnitud lain tetap:

 -Sudut antara B Dan permukaannya diubah dengan putaran spase, dengan cara ini penjana sinusoidal diperoleh:

Lebih baik jika bukannya satu gelung, nougas digunakan, dalam hal ini Fem Multiply n kali:

 Sudah tentu aliran medan magnet dapat diubah dengan gabungan bentuk -bentuk ini, walaupun ia akan menjadi lebih rumit untuk menggambarkan.

Aplikasi

Permohonan segera undang -undang Lenz adalah untuk menentukan makna Fem atau arus yang diinduksi tanpa perlu melakukan apa -apa pengiraan. Pertimbangkan yang berikut: Anda mempunyai gelung di tengah medan magnet, seperti yang menghasilkan magnet bar.

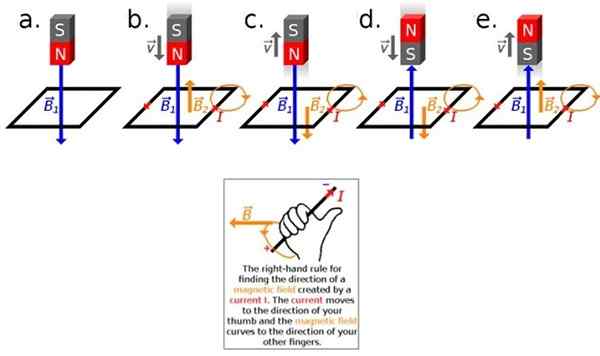Rajah 2. Permohonan Undang -undang Lenz. Sumber: Wikimedia Commons.

Sekiranya magnet dan gelung berehat satu berkenaan dengan yang lain tidak ada yang berlaku, iaitu, tidak akan ada arus yang diinduksi, kerana aliran medan magnet tetap malar dalam kes itu, (lihat Rajah 2a). Untuk mendorong arus, perlu alirannya berbeza -beza.

Sekarang, jika terdapat pergerakan relatif antara magnet dan spase, sama ada menggantikan magnet ke arah spase, atau ke arah magnet, akan ada arus yang diinduksi untuk mengukur (Rajah 2b dan seterusnya).

Arus yang disebabkan oleh ini seterusnya menjana medan magnet, oleh itu kita akan mempunyai dua bidang: iaitu magnet B₁ berwarna biru dan yang dikaitkan dengan arus yang dibuat oleh induksi B₂, dalam oren.

Penguasa ibu jari yang betul membolehkan anda mengetahui arah B₂, Untuk melakukan ini, ibu jari tangan kanan diletakkan ke arah dan arah yang ada semasa. Empat jari yang lain menunjukkan arah di mana medan magnet melengkung, mengikut Rajah 2 (di bawah).

Boleh melayani anda: cermin cembung

Pergerakan magnet melalui spase

Katakan magnet dijatuhkan ke arah gelung dengan tiang utaranya yang diarahkan ke arahnya (Rajah 3). Garis medan magnet meninggalkan tiang utara n dan masuk ke tiang selatan. Oleh itu, akan ada perubahan dalam φ, aliran yang dihasilkan oleh B₁ yang melintasi gelung:Φ kenaikan!  Oleh itu dalam gelung medan magnet dibuat B₂ Dengan niat bertentangan.

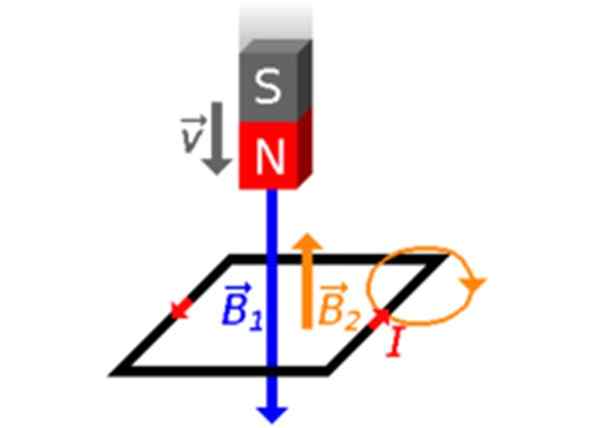Rajah 3. Magnet bergerak ke arah gelung dengan tiang utaranya kepadanya. Sumber: Wikimedia Commons.

Arus yang diinduksi membuat rasa bertentangan dengan jarum jam, -flechas merah dalam Rajah 2 dan 3-, menurut peraturan ibu jari kanan.

Mari kita mengalihkan magnet Spira dan kemudiannya Φ berkurangan (Rajah 2c dan 4), oleh itu gelung cepat membuat medan magnet di dalamnya B₂ Dengan cara yang sama, untuk mengimbangi. Oleh itu arus yang diinduksi adalah masa, seperti yang dapat dilihat dalam Rajah 4.

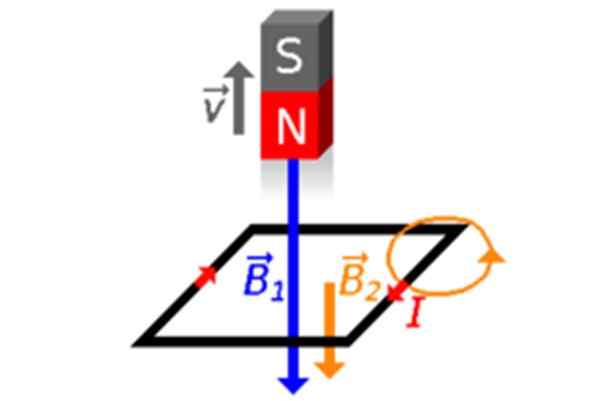Rajah 4. Magnet bergerak dari gelung, selalu dengan tiang utaranya yang menunjuk kepadanya. Sumber: Wikimedia Commons.

Melabur kedudukan magnet

Apa yang berlaku jika kedudukan magnet dilaburkan? Sekiranya tiang selatan menunjuk ke gelung, lapangan menunjuk, sejak garis -garis B Dalam magnet mereka meninggalkan Kutub Utara dan masuk ke Kutub Selatan (lihat Rajah 2D).

Segera undang -undang Lenz memaklumkan bahawa bidang menegak ini, yang dicetuskan ke arah gelung, akan mendorong medan yang bertentangan dalam hal ini, iaitu, B₂ turun dan arus yang diinduksi juga akan menjadi masa.

Akhirnya dia mengalihkan magnet la espira, selalu dengan tiang selatannya menunjuk ke pedalaman ini. Kemudian di dalam gelung ada bidang B₂ Untuk menyumbang kepada penyingkiran magnet yang tidak mengubah aliran medan di dalamnya. Begitu banyak B₁ sebagai B₂ Mereka akan mempunyai makna yang sama (lihat Rajah 2d).

Pembaca akan menyedari bahawa, seperti yang dijanjikan, tiada pengiraan telah dibuat untuk mengetahui arah arus yang diinduksi.

Eksperimen

Heinrich Lenz (1804-1865) melakukan pelbagai kerja eksperimen sepanjang karier saintifiknya. Yang paling terkenal adalah apa yang baru saja kita jelaskan, mendedikasikan diri mereka untuk mengukur kekuatan dan kesan magnet yang dicipta dengan tiba -tiba menjatuhkan magnet di tengah -tengah gelung. Dengan hasilnya, dia menyempurnakan kerja yang dilakukan oleh Michael Faraday.

Tanda negatif ini dalam undang -undang Faraday ternyata menjadi percubaan yang paling diiktiraf hari ini. Walau bagaimanapun, Lenz melakukan banyak pekerjaan dalam geofizik semasa belia dan sementara itu dia didedikasikan untuk menjatuhkan magnet di dalam giliran dan tiub. Dia juga mempelajari rintangan elektrik dan kekonduksian logam.

Khususnya, mengenai kesan kenaikan suhu dalam nilai rintangan. Dia terus memerhatikan bahawa ketika memanaskan dawai, rintangan berkurangan dan menghilangkan haba, sesuatu yang James Joule juga diperhatikan secara bebas.

Untuk selama -lamanya mengingati sumbangan mereka kepada elektromagnetisme, sebagai tambahan kepada undang -undang yang menanggung namanya, kepada induktansi (gegelung) mereka dilambangkan dengan huruf l.

Boleh melayani anda: Teorem Thévenin: Apa yang terdiri, aplikasi dan contoh

Tiub Lenz

Ini adalah percubaan di mana ia ditunjukkan sebagai hentian magnet apabila ia dikeluarkan di dalam tiub tembaga. Magnet ketika jatuh, menghasilkan variasi dalam aliran medan magnet di dalam tiub, seperti halnya dengan lingkaran kuasa.

Kemudian arus teraruh dicipta yang menentang perubahan aliran. Tiub ini menghasilkan medan magnetnya sendiri untuk ini, yang seperti yang sudah kita ketahui, dikaitkan dengan arus yang diinduksi. Katakan magnet dikeluarkan dengan Kutub Selatan ke bawah, (2d dan 5).

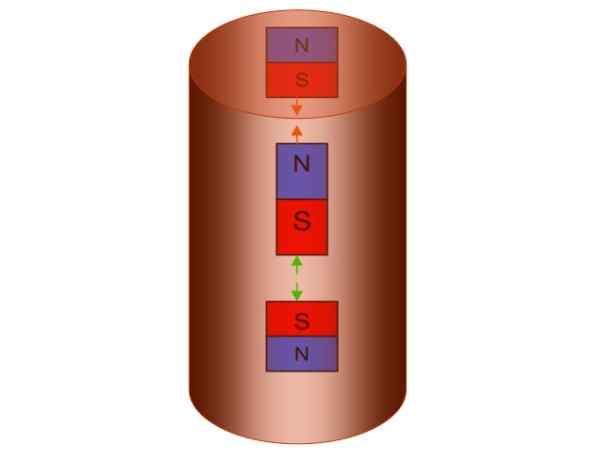Rajah 5. Tiub Lenz. Sumber: f. Zapata.

Akibatnya, tiub mencipta medan magnetnya sendiri dengan tiang utara ke bawah dan tiang selatan ke atas, yang bersamaan dengan mewujudkan beberapa magnet fiktif, satu di atas dan satu lagi di bawah yang jatuh.

Konsep ini terkandung dalam angka berikut, tetapi perlu diingat bahawa tiang magnet tidak dapat dipisahkan. Sekiranya magnet fiktif yang lebih rendah mempunyai tiang utara, ia semestinya akan menemani selatan ke atas.

Oleh kerana tiang yang bertentangan menarik dan bertentangan dengan yang bertentangan, magnet yang jatuh akan ditolak, dan pada masa yang sama tertarik dengan magnet fiksyen atas.

Kesan bersih akan sentiasa brek walaupun magnet dilepaskan dengan Kutub Utara ke bawah.

Undang-undang Joule-Lenz

Undang-undang Joule-Lenz menggambarkan sebagai sebahagian daripada tenaga yang berkaitan dengan arus elektrik yang beredar oleh pemandu hilang dalam bentuk haba, kesan yang digunakan dalam pemanas elektrik, plat, pengering rambut dan dapur elektrik, antara peralatan lain.

Kesemua mereka mempunyai rintangan, filamen atau elemen pemanasan yang memanaskan laluan semasa.

Dalam bentuk matematik, sama ada R Rintangan elemen pemanasan, Yo keamatan semasa yang beredar melaluinya dan t Masa, jumlah haba yang dihasilkan oleh Joule Effect adalah:

Q = i². R. t

Di mana Q Ia diukur dalam joules (unit SI). James Joule dan Heinrich Lenz menemui kesan ini secara serentak sekitar tahun 1842.

Contoh

Di bawah ini kita menunjukkan tiga contoh penting di mana undang-undang Faraday-Lenz digunakan:

Penjana semasa berselang -seli

Penjana semasa bergantian mengubah tenaga mekanikal menjadi tenaga elektrik. Yayasan itu diterangkan pada mulanya: gelung diputar di tengah -tengah medan magnet seragam, seperti yang dicipta antara kedua -dua tiang elektromagnet yang hebat. Apabila digunakan N spiral, yang Fem Meningkatkan secara proporsional ke N.

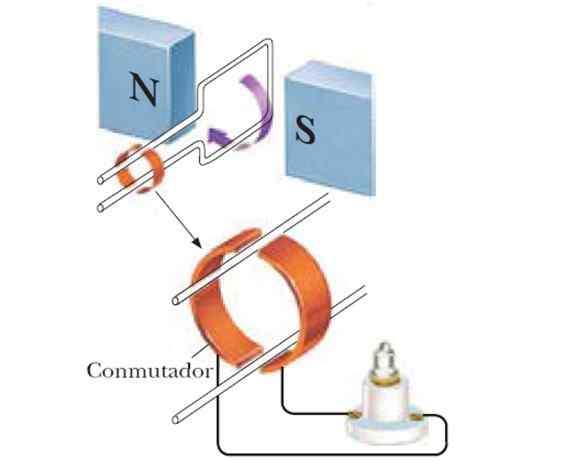Rajah 6. Penjana semasa berselang.

Apabila gelung dihidupkan, vektor biasa ke permukaannya mengubah orientasinya berkenaan dengan medan, menghasilkan a Fem yang berbeza dengan cara sinusoidal dari masa ke masa. Katakan kekerapan putaran sudut adalah Ω, Kemudian apabila menggantikan persamaan yang berlaku pada mulanya, ia akan menjadi:

Pengubah

Ia adalah peranti yang membolehkan anda mendapatkan voltan langsung dari voltan alternatif. Transformer adalah sebahagian daripada peranti yang tak terhitung jumlahnya, seperti pengecas telefon bimbit, contohnya.Ia berfungsi dengan cara berikut:

Terdapat dua gegelung yang dilancarkan di sekitar nukleus besi, satu dipanggil utama dan yang lain sekunder.  Jumlah pusingan masing -masing adalah n₁ dan n₂.

Gegelung utama atau penggulungan disambungkan ke voltan alternatif (seperti elektrik buatan sendiri, contohnya) borang V_P = V₁.cos ωt, menyebabkan arus frekuensi bergantian beredar Ω.

Arus ini berasal dari medan magnet yang seterusnya menyebabkan fluks magnet berayun pada gegelung kedua atau penggulungan, dengan voltan sekunder bentuk V_S = V₂.cos ωt.

Walau bagaimanapun, ternyata medan magnet di dalam nukleus besi adalah berkadar dengan kebalikan dari bilangan pusingan penggulungan utama:

Ia boleh melayani anda: 13 contoh undang -undang kedua Newton dalam kehidupan seharian

B ∝ 1 /n₁

Dan sebagainya akan V_P, voltan dalam penggulungan utama, sementara Fem diinduksi V_S Dalam penggulungan kedua ia berkadar, seperti yang kita ketahui, dengan jumlah giliran n₂ dan juga kepada V_P.

Oleh itu, menggabungkan perkadaran ini ada hubungan antara V_S dan V_P yang bergantung pada kuota antara jumlah giliran masing -masing, seperti berikut:

V_S = (N₂ /N₁) V_P

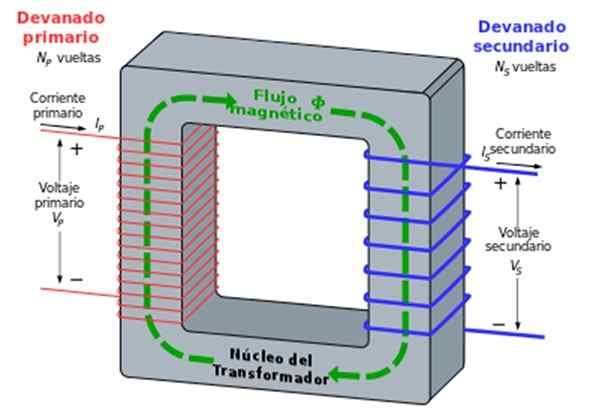Rajah 7. Pengubah. Sumber: Wikimedia Commons. Kundalinizero [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]]

Pengesan logam

Mereka adalah peranti yang digunakan di bank dan lapangan terbang keselamatan. Mereka mengesan kehadiran mana -mana logam, bukan hanya besi atau nikel. Mereka bekerja terima kasih kepada arus yang diinduksi, melalui penggunaan dua gegelung: satu pemancar dan penerima lain.

Arus frekuensi tinggi bergantian diluluskan dalam gegelung penghantaran, sehingga menghasilkan medan magnet alternatif di sepanjang paksi (lihat angka), yang mendorong arus dalam gegelung penerima, sesuatu yang lebih serupa dengan apa yang berlaku dengan pengubah.

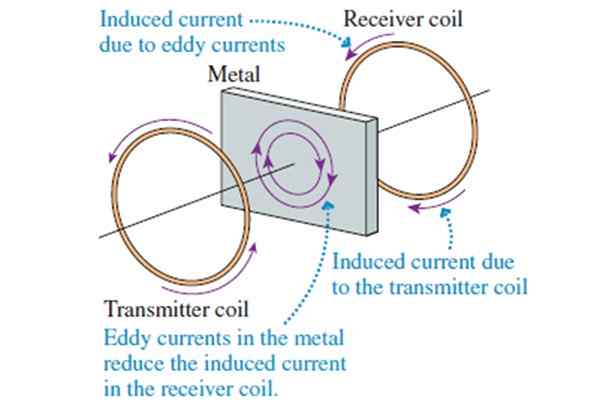Rajah 8. Prinsip Operasi Pengesan Logam.

Jika sekeping logam diletakkan di antara kedua -dua gegelung, arus teraruh kecil muncul di dalamnya, yang dipanggil arus foucault (yang tidak dapat mengalir dalam penebat). Gegelung penerimaan bertindak balas terhadap medan magnet gegelung penghantaran dan yang dicipta oleh arus Foucault.

Arus Foucault Cuba meminimumkan aliran medan magnet di bahagian logam. Oleh itu, medan yang melihat gegelung penerima, berkurangan apabila menginterposkan sekeping logam antara kedua -dua gegelung. Apabila ini berlaku penggera yang memberi amaran kehadiran logam.

Latihan

Latihan 1

Terdapat gegelung bulat dengan 250 firma radius 5 cm, terletak tegak lurus dengan medan magnet 0.2 t. Tentukan Fem disebabkan jika dalam selang waktu 0.1 s, medan magnet magnet beregu dan menunjukkan makna arus, mengikut angka berikut:

Rajah 9. SPIRA Pekeliling di tengah -tengah medan magnet seragam berserenjang dengan satah spase. Sumber: f. Zapata.

Penyelesaian

Pertama kita akan mengira magnitud FEM yang diinduksi, maka makna arus yang berkaitan akan ditunjukkan mengikut lukisan.

N = 250 giliran

A = π. R² = p . (5 x 10^-2 m)² = 0.0079 m².

cos θ = cos 0 = 1 (Vektor n Ia memerlukan selari dengan B)

Oleh kerana medan magnet menggandakan magnitudnya, anda mempunyai:

Menggantikan nilai -nilai ini dalam persamaan untuk magnitud Fem Dihidupkan:

ε = 250. 0.0079 m² . 2 t/s = 3.95 v

Oleh kerana medan telah meningkat dua kali ganda, begitu juga aliran medan magnet yang dilakukan, oleh itu dalam gelung arus yang diinduksi dicipta yang menentang peningkatan tersebut.

Medan dalam angka menunjuk ke skrin. Bidang yang dibuat oleh arus yang diinduksi mesti meninggalkan skrin, menggunakan peraturan ibu jari yang betul, ia mengikuti bahawa arus yang diinduksi adalah anti -horary.

Latihan 2

Penggulungan persegi terdiri daripada 40 pusingan 5 cm, yang menjadi 50 Hz kerap di tengah -tengah medan seragam magnitud 0.1 t. Pada mulanya gegelung berserenjang dengan medan. Apa yang akan menjadi ungkapan untuk Fem diinduksi?

Penyelesaian

Dari bahagian sebelumnya, ungkapan ini disimpulkan:

ε = n.B.Ke. Ω. dosa Ωt

A = (5 x 10^-2 m)² = 0.0025 m²

N = 40 spiral

Ω = 2π.F = 2π.50 Hz = 100p s^-1

B = 0.1 t

ε = 40 x 0.1 x 0.0025 x 100π  x sen 50.t =p . Sen 100π.t v

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Sains Fizikal Konsep. 5th. Ed. Pearson.
3. Knight, r.  2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi. Pearson.
4. Openx College. Undang -undang Induksi Faraday: Undang -undang Lenz. Diperolehi dari: OpenTextBC.Ac.
5. Fizik Libretxts. Undang -undang Lenz. Pulih dari: Phys.Libretxts.org.
6. Sears, f. (2009). Fizik Universiti Vol. 2.