Tanda Undang -undang

Kami menerangkan undang -undang tanda -tanda, dengan contoh dan latihan yang diselesaikan

Skim undang -undang tanda

Apakah undang -undang tanda?

The Tanda Undang -undang Ini adalah set peraturan yang digunakan dalam pengiraan aritmetik dan algebra dengan nombor nyata untuk memberikan tanda dengan tepat kepada hasilnya, apabila jumlah positif dan negatif terlibat.

Terdapat peraturan yang mencukupi mengikut operasi yang dijalankan: jumlah, penolakan, pendaraban dan pembahagian, yang paling asas, dan terdapat juga peraturan tanda -tanda yang berkaitan dengan potensi dan operasi pemfailan.

Dalam operasi yang diberikan, sama ada dengan tangan atau dengan kalkulator, adalah perlu untuk menerapkan undang -undang tanda -tanda dengan betul untuk memastikan hasil yang betul, kerana hanya perubahan kecil dalam tanda -tanda dengan ketara mengubah jumlahnya.

Undang -undang tanda untuk setiap operasi aritmetik asas dan kes -kes yang mungkin timbul diperiksa di bawah.

Undang -undang Tanda dalam Jumlah

1) Sekiranya nombor ditambah mempunyai tanda yang sama

Nombor ditambah seperti biasa dan hasilnya ditambah kepada tanda nombor, tanpa mengira sama ada ini positif atau negatif.

Penting untuk diingat bahawa nombor positif biasanya tidak sebelum tanda, tetapi ditulis secara langsung. Sebaliknya, nombor negatif ditulis dalam kurungan, terutamanya apabila ia didahului oleh simbol operasi aritmetik, untuk mengelakkan kekeliruan.

Contoh jumlah nombor dengan tanda yang sama:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(-3) + (-8) = -11
(-5) + (-10) + (-6) = -21

2) Sekiranya nombor yang akan ditambah mempunyai tanda yang berbeza

Nombor dikurangkan dan tanda nombor yang mempunyai nilai mutlak terbesar ditambah kepada hasilnya, sama ada positif atau negatif.

Sebagai contoh, menjalankan operasi 5 + (-14). Oleh kerana nilai mutlak (-14) adalah lebih besar daripada nilai mutlak 5, 5 unit dikurangkan dari 14, yang memberikan 9 dan hasil ini diletakkan tanda negatif:

Boleh melayani anda: prisma dan piramid

5 + (-14) = -9

Lebih banyak contoh peraturan ini yang digunakan untuk jumlah dua nombor tanda yang berbeza adalah:

(-27) + 12 = -15

12 + (-7) = 5

Sekiranya dalam operasi terdapat lebih daripada dua penambahan dengan tanda yang berbeza, Harta bersekutu dari jumlah:

(-20) + 9 + (-7) = [(-20) + 9] + (-7)

Operasi ini pertama kali dilakukan di Pracete, yang terdiri daripada jumlah dua nombor tanda yang berbeza, yang mana peraturan yang diterangkan digunakan: hasilnya dikurangkan dan tanda nombor dengan nilai mutlak tertinggi:

(-20) + 9 = -11

Operasi seperti ini:

(-20) + 9 + (-7) = (-11) + (-7)

Sekarang anda mempunyai jumlah dua nombor tanda yang sama, maka mereka biasanya ditambah dan hasilnya diletakkan sebagai tanda negatif:

(-20) + 9 + (-7) = (-11) + (-7) = -18

Tanda dalam pengganti

Penolakan dua nombor ditakrifkan sebagai jumlah yang bertentangan. Sebaliknya, sebaliknya dengan nombor dikatakan nombor dengan tanda yang diubah. Sebagai contoh, kebalikan dari 2 adalah (-2), kebalikan dari (-5) adalah 5 dan sebagainya.

Dengan ini, apabila anda mempunyai penolakan dua nombor:

A - b

Ia hanya berubah menjadi jumlah yang bertentangan dengan B:

A + ( - b)

Dan teruskan seperti yang diterangkan dalam bahagian sebelumnya. Perhatikan untuk meletakkan tanda + nombor negatif tidak mengubahnya, tetapi sangat berhati -hati, sebaliknya tidak benar.

Apabila bilangan "a", yang merupakan minuend, lebih besar daripada nombor "b", yang dicuri, beroperasi seperti dalam pengurangan nombor semula jadi. Tiada masalah, kerana sebilangan besar dikurangkan dari jumlah yang lebih kecil:

Boleh melayani anda: Ketidaksamaan segitiga: demonstrasi, contoh, latihan yang diselesaikan

25 - 8 = 17

Dengan contoh -contoh berikut, kaedah menambah yang bertentangan dengan tolak adalah sangat mudah:

(-5) - 24 = (-5) +( - 24) = - 29
32 - (-23) = 32 + 23 = 55

Undang -undang tanda dalam pendaraban

Undang -undang tanda -tanda dalam pendaraban digunakan dengan cara ini:

• Dengan mengalikan dua nombor tanda yang sama, hasilnya sentiasa positif.
• Produk dua nombor tanda bertentangan selalu negatif.

Ringkasan Peraturan Tanda untuk pendaraban ditunjukkan dalam imej:

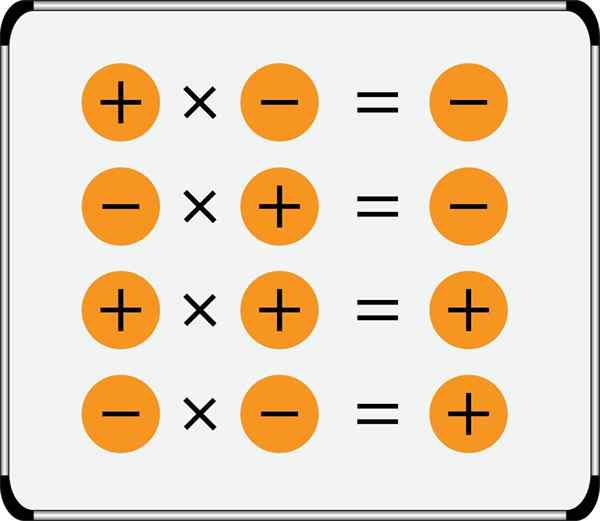
Perhatikan bahawa nombor positif boleh ditulis tanpa tanda sebelumnya, tetapi nombor negatif selalu memilikinya, sebagai tambahan, dua simbol aritmetik tidak pernah ditulis antara satu sama lain, mereka mesti selalu dipisahkan oleh kurungan, sebagai contoh:

Tidak betul: 3 × -4
Betul: 3 × (-4) = -12

(-5) × 6 = -5 × 6 = -30
(-3) × (-11) = 33
10 × 27 = 270

Untuk melipatgandakan lebih daripada dua nombor, harta pendaraban bersekutu digunakan, kerana urutan faktor tidak mengubah produk, sebagai contoh, ketika menjalankan:

(-2) × (-14) × 16

Anda boleh membiak dua faktor pertama, atau dua yang terakhir jika anda mahu, dan kemudian melipatgandakan hasilnya dengan faktor yang selebihnya. Dalam kes ini, kedua -dua faktor akan didarabkan mula -mula bermula di sebelah kiri:

[(-2) × (-14)] × 16

Produk dua nombor negatif adalah positif, kemudian (-2) × (-14) = 28 dan kekal:

28 × 16 = 448

Undang -undang Tanda Di Bahagian

Ia sama dengan peraturan tanda untuk pendaraban:

• Nisbah dua nombor tanda yang sama selalu positif.
• Dengan membahagikan dua nombor tanda sebaliknya, hasilnya selalu negatif.

Ia dapat melayani anda: perbezaan antara bulatan dan lilitan (dengan contoh)

Sebagai contoh:

24 ÷ 8 = 3
-36 ÷ 3 = -12
162 ÷ (-9) = -18
-216 ÷ (-6) = 36

Undang -undang tanda dalam pemberdayaan dan pemfailan

Eksponen nombor bertulis ialah:

keⁿ

Di mana "a" adalah asas dan "n" adalah eksponen. Dua kes dibezakan, menurut pariti eksponen:

Kes 1: A positif

Apabila asasnya positif, hasilnya positif tanpa mengira sama ada eksponen itu atau ganjil, seperti dalam:

2³ = 8
3⁴ = 81

Kes 2: A adalah negatif

Berikut adalah dua kes:

• Apabila eksponennya, maka hasilnya positif.
• Sekiranya eksponennya ganjil, ia adalah negatif.

Contoh

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(-2)⁴ = (-2) ∙ (-2) ∙ (-2) ∙ (-2) = 16
(-3)³ = (-3) ∙ (-3) ∙ (-3) = -27

Operasi dengan simbol kumpulan

Mereka sering muncul operasi berasingan dengan simbol pengelompokan: tanda kurung, kurungan dan kunci. Ini dihapuskan dari dalam keluar dengan mengambil kira perkara berikut:

• Sekiranya simbol pengelompokan didahului dengan tanda positif, ia boleh dikeluarkan tanpa mengubah tanda -tanda kandungan, contohnya: + (-3 + 5 - 1) = -3 + 5 - 1 = 1.
• Jika tanda negatif mendahului simbol kumpulan, ia ditarik balik dengan melabur tanda kandungan, contohnya: - (-3 + 5 -1) = 3 - 5 + 1 = -1.
• Apabila terdapat gabungan operasi jumlah, penolakan, pendaraban dan pembahagian, sifat bersekutu dan pengedaran boleh digunakan untuk kemudahan.

Latihan yang diselesaikan

a) 10 + 10

Penyelesaian: 20

b) (-8) + (-3)

Penyelesaian: -11

c) (3) + (-10) 

Penyelesaian: -7

d) (5) x (-3)

Penyelesaian: -15

e) (-10) x (-10)

Penyelesaian: 100

f) (18) ÷ (-3)

Penyelesaian: -6

G) (-10) ÷ (-2)

Penyelesaian: 5

h) 4 - ( - 7 + 9)

Penyelesaian: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11- 9 = 2