Ciri -ciri garis tegak lurus, contoh, latihan

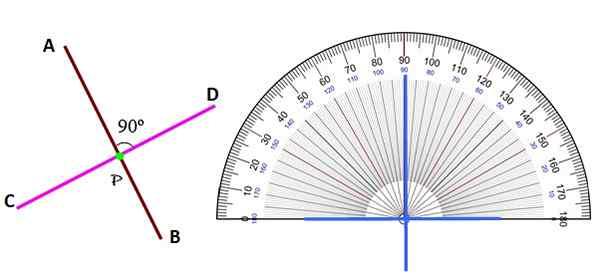
A garis tegak lurus Ia adalah salah satu yang membentuk sudut 90º berkenaan dengan garis, lengkung atau permukaan lain. Perhatikan bahawa apabila dua baris berserenjang dan pada satah yang sama, apabila dipotong, mereka membentuk empat sudut yang sama, masing -masing 90º.

Sekiranya salah satu sudut tidak 90º dikatakan bahawa garis adalah serong. Garis tegak lurus sering dalam reka bentuk, seni bina dan pembinaan, contohnya rangkaian paip imej berikut.

Rajah 1. Paip lurus dan banyak garis tegak lurus. Berapa sudut 90º yang dapat dikira dalam gambar ini? Sumber: PIQSELS.

Orientasi garis tegak lurus boleh beragam, seperti yang ditunjukkan di bawah:

Rajah 2. Garis tegak lurus di atas kapal terbang. Sumber: f. Zapata.

Tidak kira kedudukannya, garis tegak lurus diiktiraf dengan mengenal pasti sudut di antara mereka sebagai 90º, dengan bantuan penghantar.

Perhatikan bahawa tidak seperti garis selari dalam satah, yang tidak pernah bersilang, tegak lurus selalu melakukannya pada titik p, yang dipanggil kaki salah satu baris di sisi lain. Oleh itu dua garis tegak lurus juga Secantes.

Mana -mana baris mempunyai tegak lurus yang tidak terhingga, kerana dengan hanya menggantikan segmen ab ke kiri atau kanan di segmen CD, kita akan berserenjang baru dengan kaki yang lain.

Walau bagaimanapun, tegak lurus yang melepasi hanya melalui titik tengah segmen dipanggil Bisector segmen tersebut.

[TOC]

Contoh garis tegak lurus

Garis tegak lurus sering di landskap bandar. Dalam imej berikut (Rajah 3) hanya beberapa garis tegak lurus yang dihargai pada fasad mudah bangunan ini dan unsur -unsurnya seperti pintu, saluran, langkah dan banyak lagi: Lagi:

Boleh melayani anda: Fourier Diperbaharui diubah: sifat, aplikasi, contoh Rajah 3. Terdapat banyak garis tegak lurus di fasad bangunan biasa seperti ini. Sumber: Richard Kang Melalui Flickr.

Perkara yang baik ialah tiga baris berserenjang antara satu sama lain membantu kami menubuhkan lokasi titik dan objek di ruang angkasa. Adalah paksi koordinat yang dikenal pasti sebagai X paksi, Paksi y dan Z paksi, Jelas kelihatan di sudut bilik segi empat seperti yang berikut:

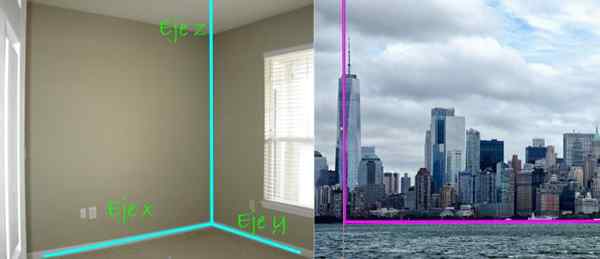Rajah 4. Sistem paksi Cartesian terdiri daripada tiga baris yang berserenjang antara satu sama lain, masing -masing mempunyai arah keutamaan di ruang angkasa. Kredit Imej Kiri: Treybunn 2 melalui Flickr. Imej yang betul; Needpix.

Dalam pemandangan panorama kota, di sebelah kanan, keseragaman antara pencakar langit dan tanah juga diberi amaran. Yang pertama akan mengatakan bahawa ia dijumpai di seluruh Z paksi, Walaupun tanah adalah pesawat, yang dalam kes ini adalah pesawat Xy.

Sekiranya tanah membentuk kapal terbang Xy, Pencakar langit juga berserenjang dengan mana -mana jalan atau jalan, yang menjamin kestabilannya, kerana struktur cenderung tidak stabil.

Dan di jalan -jalan, di mana sahaja sudut segi empat tepat, terdapat garis tegak lurus. Banyak jalan dan jalan -jalan mempunyai susun atur tegak lurus, dengan syarat kemalangan tanah dan geografi membenarkannya.

Tiba -tiba menyatakan keseragaman antara garis, segmen atau vektor, simbol ⊥ digunakan. Contohnya, jika garis l₁ berserenjang dengan garis l₂, Kami menulis:

L₁ ⊥ l₂

Lebih banyak contoh garis tegak lurus

- Dalam reka bentuk garis tegak lurus adalah sangat hadir, kerana banyak objek biasa didasarkan pada dataran dan segi empat tepat. Quadrilaterals ini dicirikan dengan mempunyai sudut dalaman 90º, kerana sisi mereka adalah dua hingga dua selari:

Ia boleh melayani anda: Persamaan Parabola Umum (contoh dan latihan)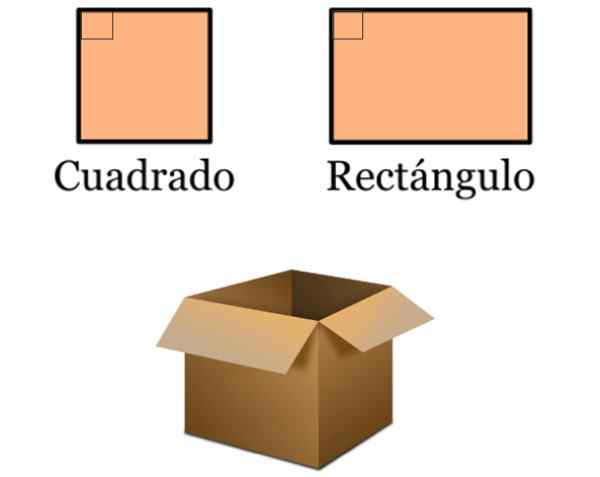 Rajah 5. Squares dan Rectangles adalah sebahagian daripada banyak reka bentuk, seperti kotak kadbod mudah ini untuk menyimpan barangan. Sumber: f. Zapata.

- Mahkamah di mana sukan yang berlainan diamalkan diamalkan oleh banyak dataran dan segi empat tepat. Ini seterusnya mengandungi garis tegak lurus.

- Dua segmen yang membentuk segitiga segi empat tepat berserenjang antara satu sama lain. Ini dipanggil kategori, sementara garis yang tinggal dipanggil Hypotenuse.

- Garis vektor medan elektrik berserenjang dengan permukaan keseimbangan elektrostatik.

- Untuk pemacu yang dimuatkan, peralatan dan peralatan sentiasa tegak lurus dengan medan elektrik.

- Dalam sistem paip atau saluran yang digunakan untuk mengangkut pelbagai jenis cecair, seperti gas yang muncul dalam Rajah 1, adalah perkara biasa bagi siku pada sudut tepat. Oleh itu, mereka membentuk garis tegak lurus, demikian adalah kes bilik dandang:

Rajah 6. Paip di bilik dandang. Sumber: Wikimedia Commons. Roger McLassus/CC BY-S (http: // creativeCommons.Org/lesen/by-sa/3.0/)

Latihan

- Latihan 1

Lukis dua garis tegak lurus dengan peraturan dan kompas.

Penyelesaian

Sangat mudah dilakukan, mengikuti langkah -langkah ini:

-Baris pertama ditarik, dipanggil AB (hitam).

-Di atas (atau di bawah jika disukai) dari titik AB Point P, di mana tegak lurus akan berlalu. Sekiranya P berada di atas (atau di bawah) separuh daripada AB, kata tegak lurus adalah bisektor segmen ab.

-Dengan kompas yang berpusat pada p, bulatan ditarik yang memotong ab dalam dua mata, dipanggil ke 'dan b' (merah).

Boleh melayani anda: Nombor mesra atau mesra: Contoh dan bagaimana mencarinya

-Kompas di A'p dibuka, ia memberi tumpuan kepada 'dan bulatan ditarik yang melalui p (hijau).

-Ulangi langkah sebelumnya, tetapi kini membuka kompas panjang segmen b'p (hijau). Kedua -dua lengkungan lilitan dipotong pada titik q di bawah p dan tentu saja di yang terakhir.

-Mata p dan q disertai dengan peraturan dan garis tegak lurus (biru) sudah siap.

-Akhirnya, semua pembinaan tambahan mesti dipadamkan dengan teliti, hanya meninggalkan tegak lurus.

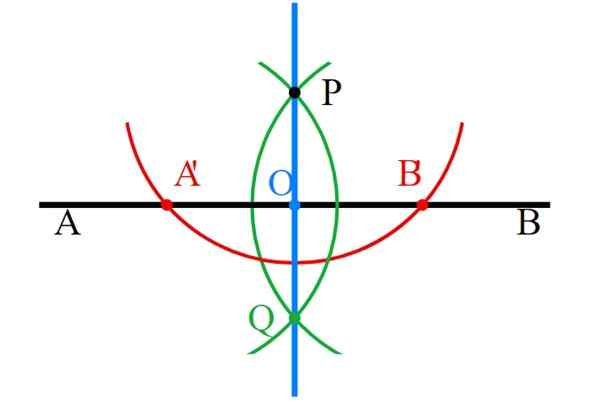Rajah 6. Garis -garis yang bertekanan dengan peraturan dan kompas. Sumber: Wikimedia Commons.

- Latihan 2

Dua baris l₁ dan l₂ Mereka berserenjang jika lereng masing -masing m₁ dan m₂ Mereka memenuhi hubungan ini:

m₁ = -1/m₂

Memandangkan garis y = 5x - 2, cari garis tegak lurus kepadanya dan lulus titik (-1, 3).

Penyelesaian

-Pertama sekali ialah cerun garis tegak lurus m_⊥, Seperti yang ditunjukkan dalam pernyataan. Lereng garis asal adalah m = 5, pekali yang mengiringi "x". Jadi:

m_⊥= -1/5

-Kemudian persamaan garis tegak lurus dibina dan_⊥, Menggantikan nilai yang telah dijumpai sebelum ini:

dan_⊥= -1/5x + b

-Kemudian nilai b ditentukan, dengan bantuan titik yang diberikan oleh pernyataan, (-1,3), kerana garis tegak lurus mesti melaluinya:

y = 3

x = -1

Mengganti:

3 = -1/5 (-1) + b

Nilai B dibersihkan:

B = 3- (1/5) = 14/5

-Akhirnya persamaan akhir dibina:

dan_⊥= -1/5x + 14/5

Rujukan

1. Baldor, a. 2004. Geometri rata dan ruang. Penerbitan Kebudayaan.
2. Clemens, s. 2001. Geometri dengan aplikasi dan penyelesaian masalah. Addison Wesley.
3. Matematik menyeronokkan. Garis tegak lurus. Pulih dari: Mathisfun.com.
4. Institut Monterey. Garis tegak lurus. Pulih dari: Montereyinstitute.org.
5. Wikipedia. Garis tegak lurus. Pulih dari: Adakah.Wikipedia.org.