Matematik diskret

Apakah matematik diskret?

The Matematik diskret sesuai dengan bidang matematik yang bertanggungjawab untuk mengkaji set nombor semulajadi; iaitu, set nombor perakaunan terhingga dan tak terhingga di mana unsur -unsur boleh dikira secara berasingan, satu demi satu.

Set ini dikenali sebagai set diskret; Contoh set ini adalah nombor keseluruhan, graf atau ekspresi logik, dan digunakan dalam bidang sains yang berlainan, terutamanya dalam sains komputer atau pengkomputeran.

Penerangan

Dalam matematik diskret, prosesnya boleh diubah, mereka berdasarkan keseluruhan nombor. Ini bermakna nombor perpuluhan tidak digunakan dan, oleh itu, pendekatan atau had, seperti di kawasan lain, tidak digunakan sama ada. Sebagai contoh, yang tidak diketahui boleh sama dengan 5 atau 6, tetapi tidak pernah 4.99 atau 5.9.

Sebaliknya, dalam perwakilan grafik pembolehubah akan diskret dan diberikan dari satu set titik terhingga, yang dikira satu demi satu, seperti yang diperhatikan dalam imej:

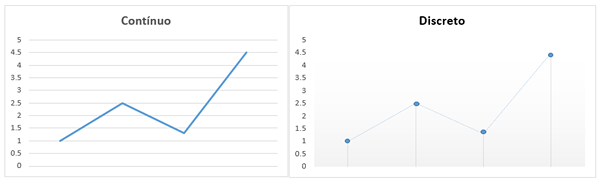
Matematik Diskret dilahirkan kerana keperluan untuk mendapatkan kajian yang tepat yang boleh digabungkan dan terbukti, untuk menerapkannya di kawasan yang berbeza.

Untuk apa matematik diskret?

Matematik diskret digunakan di pelbagai kawasan. Antara yang utama adalah seperti berikut:

Combinatorial

Kajian set terhingga di mana unsur -unsur boleh dipesan atau digabungkan dan ditarik balik.

Teori pengedaran diskret

Peristiwa kajian yang berlaku di ruang di mana sampel boleh menjadi perakaunan, di mana pengagihan berterusan digunakan untuk mendekati pengagihan diskret, atau bertentangan.

Teori Maklumat

Ia merujuk kepada pengekodan maklumat, yang digunakan untuk reka bentuk dan penghantaran dan penyimpanan data, seperti isyarat serupa.

Boleh melayani anda: Kaedah Trachtenberg: Apa itu, Contohnya

Pengkomputeran

Melalui matematik yang bijak, masalah diselesaikan menggunakan algoritma, serta apa yang dapat dikira dan masa yang diperlukan untuk melakukannya (kerumitan).

Kepentingan matematik diskret di kawasan ini telah meningkat dalam beberapa dekad kebelakangan ini, terutama untuk pembangunan pengaturcaraan dan Perisian.

Kriptografi

Ia berdasarkan matematik yang bijak untuk mewujudkan struktur keselamatan atau kaedah penyulitan. Contoh aplikasi ini adalah kata laluan, menghantar bit berasingan yang mengandungi maklumat.

Melalui kajian sifat -sifat bilangan dan nombor utama (teori nombor) dapat dibuat atau dimusnahkan.

Logik

Struktur diskret digunakan, yang biasanya membentuk satu set terhingga, untuk menunjukkan teorema atau, sebagai contoh, mengesahkan perisian.

Teori graf

Ia membolehkan resolusi masalah logik, menggunakan nod dan garis yang membentuk jenis graf, seperti yang ditunjukkan dalam imej berikut:

Algebra

Ia adalah kawasan yang berkait rapat dengan matematik yang bijak kerana ungkapan algebra adalah bijaksana. Melalui litar elektronik ini, pemproses, pengaturcaraan (algebra boolean) dan pangkalan data (algebra relasi) dibangunkan (algebra relasi).

Geometri

Kaji sifat gabungan objek geometri, seperti lapisan kapal terbang. Sebaliknya, geometri pengiraan memungkinkan untuk mengembangkan masalah geometri dengan menggunakan algoritma.

Tetapkan teori

Dalam matematik diskret set (terhingga dan tak terhingga) adalah objektif objektif utama. Teori Set diterbitkan oleh George Cantor, yang menunjukkan bahawa semua set tak terhingga adalah saiz yang sama.

Satu set adalah sekumpulan elemen (nombor, benda, haiwan dan orang, antara lain) yang ditakrifkan dengan baik; ia.

Boleh melayani anda: sifat kesamaan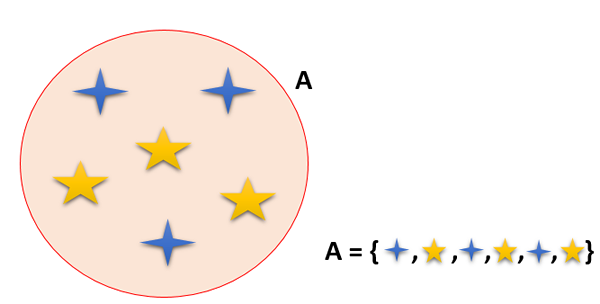

Dalam matematik terdapat set yang berbeza yang kumpulan nombor tertentu mengikut ciri -ciri mereka. Oleh itu, sebagai contoh, mereka mempunyai:

- Set nombor semulajadi n = 0, 1, 2, 3, 4, 5, 6, ... +∞.

- Set nombor keseluruhan e = - ..., -3, -2, -1, 0, 1, 2, 3, ... +∞.

- Subset nombor rasional q* = -∞ ..., - ¼, - ½, 0, ¼, ½, ... ∞.

- Set nombor sebenar r = -½, -½, -1, 0, ½, 1, ... ∞.

Set dinamakan dengan huruf abjad, dalam huruf besar; Walaupun unsur -unsur dinamakan dalam huruf kecil, di dalam kekunci () dan dipisahkan oleh koma (,). Mereka biasanya diwakili pada gambar rajah seperti Venn dan Caroll, dan juga pengkomputeran.

Dengan operasi asas seperti kesatuan, persimpangan, pelengkap, perbezaan dan produk Cartesian, set dan unsur -unsur mereka diuruskan, berdasarkan hubungan kepunyaan.

Terdapat beberapa jenis set, yang paling banyak dikaji dalam matematik diskret adalah seperti berikut:

Set terhingga

Ia adalah satu yang mempunyai bilangan elemen yang terbatas dan yang sepadan dengan nombor semula jadi. Oleh itu, sebagai contoh, a = 1, 2, 3.4 adalah set terhingga yang mempunyai 4 elemen.

Set Perakaunan Infinite

Ia adalah satu di mana terdapat surat -menyurat antara unsur -unsur set dan nombor semula jadi; iaitu, dari elemen semua elemen set dapat disenaraikan secara berturut -turut.

Dengan cara ini, setiap elemen akan sesuai dengan setiap elemen set nombor semula jadi. Sebagai contoh:

Seluruh nombor keseluruhan z = ... -2, -1, 0, 1, 2 ... boleh disenaraikan sebagai z = 0, 1, -1, 2, -2 .... Dengan cara ini adalah mungkin untuk membuat satu surat -menyurat antara unsur -unsur z dan nombor semula jadi, seperti yang dapat dilihat dalam imej berikut:

Boleh melayani anda: Pengiraan pendekatan menggunakan perbezaan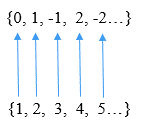

Pengunduran

Ini adalah kaedah yang digunakan untuk menyelesaikan masalah berterusan (model dan persamaan) yang mesti ditukar menjadi masalah diskret, di mana penyelesaiannya diketahui dengan pendekatan untuk penyelesaian masalah berterusan.

Melihat sebaliknya, discretization cuba untuk mendapatkan jumlah terhingga set mata tak terhingga; Dengan cara ini, unit berterusan berubah menjadi unit individu.

Umumnya kaedah ini digunakan dalam analisis berangka, seperti dalam penyelesaian persamaan pembezaan, melalui fungsi yang diwakili oleh jumlah data yang terhingga dalam domainnya, walaupun ini berterusan.

Satu lagi contoh discretization adalah penggunaannya untuk menukar analogi dengan isyarat digital, apabila unit isyarat berterusan ditukar menjadi unit individu (mereka diskriminasi), dan kemudian dikodkan dan dikira untuk mendapatkan isyarat digital.

Rujukan

1. Grimaldi, r. P. (1997). Matematik diskret dan gabungan. Editorial Addison Wesley Iberoamericana.
2. Ferrando, v. Gregori. (Sembilan-belas sembilan puluh lima). Matematik diskret. Reverte.
3. Jech, t. (2011). Tetapkan teori. Stanford Encyclopedia of Falsafah.
4. José Francisco Villalpando Becerra, a. G. (2014). Matematik Diskret: Aplikasi dan Latihan. Kumpulan Editorial Patria.
5. Landau, r. (2005). Pengkomputeran, Kursus Pertama di Saintifik.
6. Merayo, f. G. (2005). Matematik diskret. Editorial Thomson.
7. Rosen, k. H. (2003). Matematik diskret dan aplikasinya. Editorial McGraw-Hill.
8. Schneider, d. G. (Sembilan-belas sembilan puluh lima). Pendekatan logik untuk matematik diskret.