Laman utama
Fizikal
Momen formula inersia, persamaan dan contoh pengiraan

Fizikal

Momen formula inersia, persamaan dan contoh pengiraan

Dia momen inersia Dari badan tegar berkenaan dengan paksi putaran tertentu, ia mewakili rintangannya untuk mengubah halaju sudutnya di sekitar paksi itu. Ia berkadar dengan jisim dan juga ke lokasi paksi putaran, kerana badan, menurut geometrinya, lebih mudah berputar di sekitar paksi tertentu daripada yang lain.

Katakan objek yang luas (terdiri daripada banyak zarah) yang boleh berputar di sekitar paksi. Katakan tindakan bertindak F, secara tangen digunakan untuk elemen massa Δm_Yo, yang menghasilkan tork atau momen, diberikan oleh τ_jaring= Σr_Yo x F_Yo. Vektor r_Yo Ia adalah kedudukan Δm_Yo(Lihat Rajah 2).

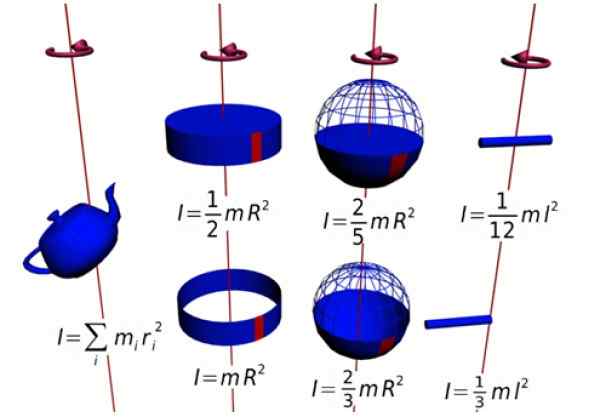
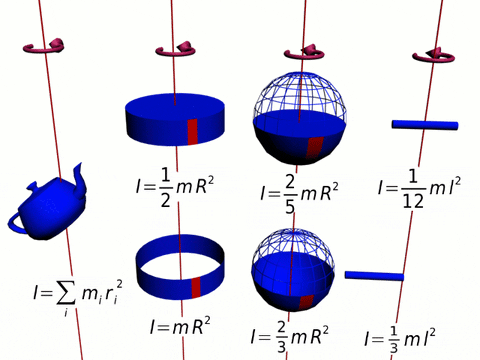Rajah 1. Detik inersia dari beberapa angka. Sumber: Wikimedia Commons.

Momen ini berserenjang dengan satah putaran (alamat +K = meninggalkan kertas). Oleh kerana kekuatan dan kedudukan radial sentiasa berserenjang, produk silang tetap:

τ_jaring = Σ f_Yo r_Yo k = Σ (Δm_Yoke_Yo) r_Yok = Σ Δm_Yo(Kepada_Yo r_Yo) k

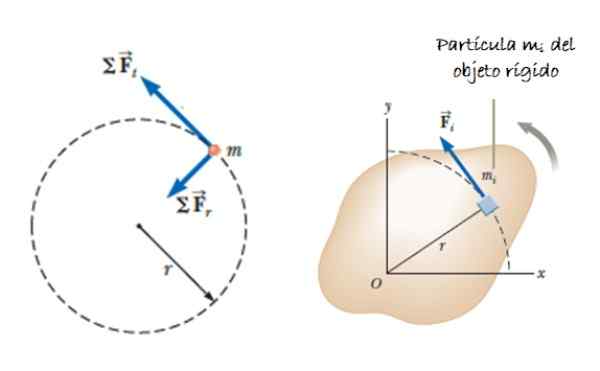Rajah 2. Zarah milik pepejal tegar dalam putaran. Sumber: Serway, r. 2018. Fizik untuk Sains dan Kejuruteraan. Jilid 1. Pembelajaran Cengage.

Pecutan a_Yo mewakili komponen pecutan tangen, kerana pecutan radial tidak menyumbang kepada tork. Bergantung pada pecutan sudut α, kita dapat menunjukkan bahawa:

ke_Yo = α r_Yo

Oleh itu tork bersih seperti ini:

τ_jaring = Σ Δm_Yo(α r_Yo²) K = (Σ r_Yo² Δm_Yo) α k

Percepatan sudut α adalah sama untuk keseluruhan objek, oleh itu ia tidak terjejas oleh subskrip "I" dan boleh meninggalkan jumlah, yang tepatnya momen inersia objek yang dilambangkan dengan huruf I:

I = Σ r_Yo² Δm_Yo

Inilah momen inersia pengedaran massa diskret. Apabila pengedaran berterusan, jumlahnya digantikan dengan integral dan Δm menjadi perbezaan massa DM. Integral dibuat di atas semua objek:

I = ∫_M(r²) Dm

Unit momen inersia dalam sistem antarabangsa jika mereka kg x m². Ia adalah jumlah skalar dan positif, kerana ia adalah hasil doh oleh kuadrat jarak jauh.

[TOC]

Contoh pengiraan

Objek lanjutan, seperti bar, cakera, sfera atau lain -lain, yang ketumpatannya ρ Ia tetap dan mengetahui bahawa ketumpatan adalah jisim - jumlah quotient, pembezaan massa DM Ia ditulis sebagai:

ρ = dm/dv → dm = ρDv

Menggantikan integral untuk masa inersia, kita ada:

I = ∫r² ρdv = ρ ∫r²Dv

Ini adalah ungkapan umum, sah untuk objek tiga dimensi, yang jumlahnya V dan kedudukan r Mereka adalah fungsi koordinat ruang x, dan dan z. Perhatikan bahawa tetap, ketumpatan adalah dari integral.

Ketumpatan ρ Ia juga dikenali sebagai ketumpatan volumetrik, tetapi jika objeknya sangat rata, sebagai lembaran atau sangat nipis dan sempit sebagai rod, bentuk ketumpatan lain boleh digunakan, mari kita lihat:

Boleh melayani anda: pergerakan putaran bumi

- Untuk lembaran yang sangat halus, ketumpatan yang digunakan adalah σ, ketumpatan permukaan (jisim per unit kawasan) dan memberi adalah pembezaan kawasan.

- Dan jika ia adalah bar nipis, di mana hanya panjang yang relevan, ketumpatan massa linear digunakan λ dan perbezaan panjang, mengikut paksi yang digunakan sebagai rujukan.

Dalam contoh berikut, semua objek dianggap tegar (tidak dapat ditentukan) dan mempunyai ketumpatan seragam.

Momen inersia bar nipis berkenaan dengan paksi yang melewati pusatnya

Di sini kita akan mengira momen inersia bar nipis, tegar, homogen, panjang l dan massa m, berkenaan dengan paksi yang melalui cara.

Di tempat pertama adalah perlu untuk menubuhkan sistem koordinat dan membina angka dengan geometri yang mencukupi, seperti ini:

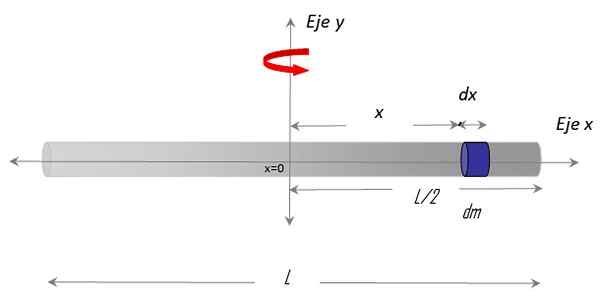Rajah 3. Geometri untuk mengira momen inersia batang nipis berkenaan dengan paksi menegak yang melewati pusatnya. Sumber: f. Zapata.

Dia dipilih X paksi di sepanjang bar dan Paksi y sebagai paksi putaran. Prosedur untuk mewujudkan integral juga memerlukan memilih perbezaan massa di bar, yang dipanggil DM, yang mempunyai panjang pembezaan Dx dan terletak di kedudukan x sewenang -wenangnya, berkenaan dengan pusat x = 0.

Menurut definisi ketumpatan massa linear λ:

λ = m/l

Apabila ketumpatan seragam, yang sah untuk m dan l, ia juga untuk DM dan DX:

λ = dm/dx → dm = λdx.

Sebaliknya, elemen massa berada dalam kedudukan x, Kemudian dengan menggantikan geometri ini dalam definisi, kita mempunyai integral yang pasti, yang batasnya adalah ekstrem bar mengikut sistem koordinat:

$I=\int _Mr^2dm =\int_\frac-L2^\fracL2x^2\lambda dx=\lambda \left [\fracx^33 \right ]_\frac-L2^\fracL2=\frac\lambda 3\left [ \fracL^38-\left ( \frac-L^38 \right ) \right ]=\frac\lambda 12L^3$

Menggantikan ketumpatan linear λ = m/l:

$I=\frac112ML^2$

Untuk mencari momen inersia bar berkenaan dengan paksi putaran lain, contohnya satu yang melewati salah satu hujungnya, anda boleh menggunakan teorem Steiner (lihat senaman yang diselesaikan pada akhir) atau melakukan pengiraan langsung yang serupa dengan itu ditunjukkan di sini, tetapi mengubahsuai geometri dengan betul.

Momen inersia album berkenaan dengan paksi yang melewati pusatnya

Album yang sangat nipis, ketebalan hina adalah tokoh rata. Sekiranya adunan diedarkan secara seragam di seluruh kawasan A, ketumpatan massa σ adalah:

σ = M/a

Begitu banyak DM sebagai memberi sesuai dengan jisim dan kawasan cincin pembezaan yang ditunjukkan dalam angka tersebut. Kami akan mengandaikan bahawa keseluruhan set berkisar di sekitar paksi dan.

Anda boleh membayangkan bahawa album itu terdiri bahawa banyak cincin sepusat radio r, masing -masing dengan momen inersia masing -masing. Menambah sumbangan semua cincin sehingga anda sampai ke radio R, Anda akan mempunyai jumlah inersia album.

σ = dm/da → dm = σmemberi

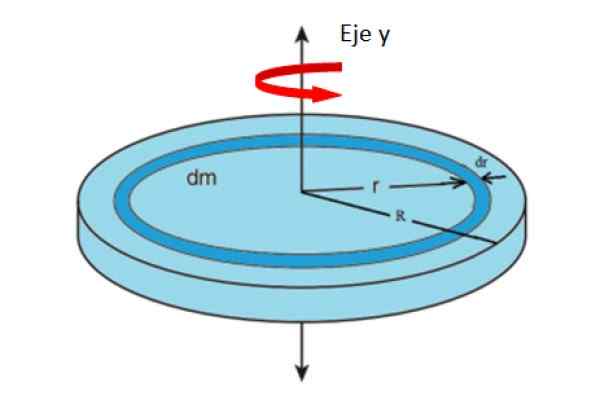Rajah 4. Geometri untuk mengira momen inersia album, berkenaan dengan paksi paksi. Sumber: f. Zapata.

Di mana m mewakili keseluruhan adunan album. Kawasan album bergantung pada jejari r sebagai:

Dapat melayani anda: kelajuan penyebaran gelombang

A = π.r²

Memperoleh mengenai R:

Da /dr = 2 = 2π.R → da = 2π.rdr

Menggantikan perkara di atas dalam definisi i:

$I=\int _Mr^2dm=\int_0^Rr^2\left (\sigma dA \right )=\sigma \int_0^Rr^2\left (2\pi rdr \right )=2\pi \sigma \int_0^Rr^3dr$ Selepas menilai hasil yang penting:

$I=2\pi \sigma \fracR^44$

Menggantikan σ = m/(π.R²) ditinggalkan:

$I=2\pi \sigma \fracR^44=2\pi\left (\fracM\pi R^2 \right )\left (\fracR^44 \right )=\frac12MR^2$

Momen inersia sfera pepejal berkenaan dengan diameter

Lingkaran radius r boleh dianggap sebagai satu siri cakera yang disusun di atas satu sama lain, di mana setiap album massa infinitesimal DM, radio r dan ketebalan Dz, Ia mempunyai momen inersia yang diberikan oleh:

memberi_cakera = (½) r²DM

Untuk mencari perbezaan ini, formula bahagian sebelumnya hanya diambil dan diganti M dan R oleh DM dan r, masing -masing. Album seperti ini dapat dilihat dalam geometri Rajah 5.

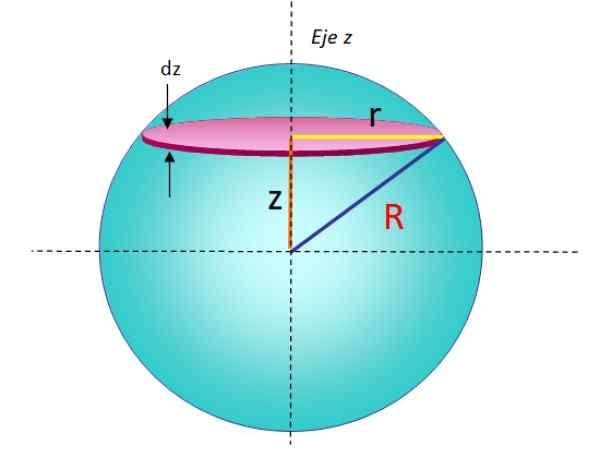Rajah 5. Geometri untuk mengira momen inersia sfera jejari pepejal berkenaan dengan paksi yang melalui diameter. Sumber: f. Zapata.

Dengan menambahkan semua momen inersia infinitesimal cakera yang disusun, momen jumlah inersia sfera diperolehi:

Yo_sfera = ∫di_cakera

Yang bersamaan dengan:

I = ∫_sfera(½) r²DM

Untuk menyelesaikan integral, anda perlu menyatakan DM betul. Seperti biasa, ia dicapai dari ketumpatan:

ρ = m/v = dm/dv → dm = ρ.Dv

Jumlah cakera perbezaan adalah:

Dv = kawasan asas x ketinggian

Ketinggian album adalah ketebalan Dz, Walaupun kawasan asas adalah πr², Oleh itu:

Dv = πr²Dz

Dan menggantikan yang bersepadu akan menjadi seperti ini:

I = ∫_sfera(½) r²Dm = ∫ (½) r²(ρπr²Dz)

Tetapi sebelum mengintegrasikan, ia mesti. Melalui teorem Pythagoras:

R² = r² + z² → R² = R² - z²

Itu membawa kita ke:

I = ∫_sfera(½) ρ r²(πr²dz) = ∫_sfera(½) ρ π r⁴Dz= ∫_sfera(½) ρ π (r² - z²)² Dz

Untuk mengintegrasikan keseluruhan sfera, kami melihat bahawa Z berbeza antara -r dan r, oleh itu:

$I=\frac12\pi \rho \left [\int_-R^RR^4dz-\int_-R^R2R^2z^2dz+\int_-R^Rz^4dz \right ]$
$I=\frac12\pi \rho \left [R^4z-2R^2\left (\fracz^33 \right )+\fracz^55 \right ]_-R^R=\frac815\pi \rho R^^5$

Mengetahui bahawa ρ = m/v = m/[(4/3) πr³] Akhirnya, ia diperolehi, setelah memudahkan:

$I=\frac815\pi \left (\fracM\frac43\pi R^3 \right )R^5=\frac25MR^2$

Momen inersia silinder pepejal berkenaan dengan paksi paksi

Untuk objek ini kaedah yang serupa dengan yang digunakan untuk sfera digunakan, hanya kali ini lebih mudah jika silinder dibayangkan untuk kerang silinder radio r, ketebalan Dr dan ketinggian H, Seolah -olah mereka adalah lapisan bawang.

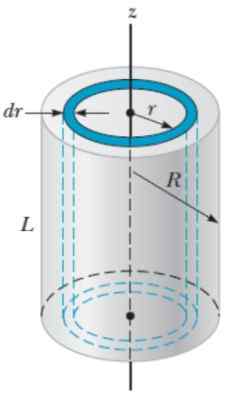Rajah 6. Geometri untuk mengira momen inersia silinder radius pepejal menghormati paksi paksi. Sumber: Serway, r. 2018. Fizik untuk Sains dan Kejuruteraan. Jilid 1. Cengage.

Kelantangan Dv lapisan silinder adalah:

Dv = 2π.Rl.Dr

Oleh itu jisim cascaron adalah:

Boleh melayani anda: Skala mikroskopik: sifat, kiraan zarah, contoh

Dm = ρ.Dv = ρ. 2π.r.L.Dr

Ungkapan ini digantikan dalam definisi momen inersia:

$I=\int _Mr^2dm = \int_0^Rr^22\pi \rho Lrdr=2\pi \rho L\int_0^Rr^3dr=2\pi \rho L\left (\fracR^44 \right )$ Memandangkan itu ρ = m / (π.R²L) ditinggalkan:

$I=2\pi \left (\fracM\pi R^2L \right ) L\left (\fracR^44 \right )=\frac12MR^2$

Persamaan sebelumnya menunjukkan bahawa momen inersia silinder tidak bergantung pada panjangnya, tetapi pada jisimnya dan radiusnya sahaja. Yeah L berubah, momen inersia berkenaan dengan paksi paksi akan terus sama. Atas sebab ini, Yo silinder bertepatan dengan album nipis yang dikira sebelumnya.

Momen inersia lembaran segi empat tepat berkenaan dengan paksi yang melewati pusatnya

The Paksi y Mendatar sebagai paksi putaran. Angka di bawah menunjukkan geometri yang diperlukan untuk menjalankan integrasi:

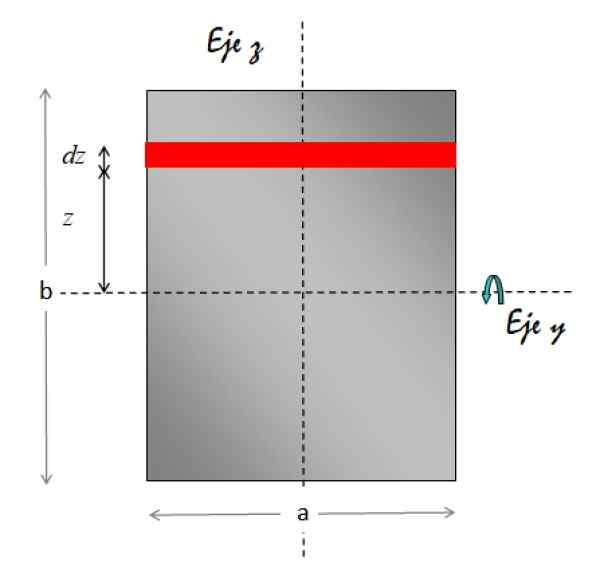Rajah 7. Geometri untuk pengiraan momen inersia plat segi empat tepat berkenaan dengan paksi selari ke lembaran dan yang melalui pusatnya. Sumber: f. Zapata.

Elemen kawasan yang ditunjukkan dalam warna merah adalah segi empat tepat. Kawasannya adalah ketinggian x asas, oleh itu:

da = a.Dz

Oleh itu perbezaan massa adalah:

Dm = σ.da = σ.(Kepada.Dz)

Bagi jarak elemen kawasan ke paksi putaran, selalu z. Kami menggantikan semua ini dalam integral momen inersia:

$I=\int _Mz^2dm=\int_\frac-b2^\fracb2z^2\left (\sigma adz \right )=\sigma a\int_\frac-b2^\fracb2z^2dz=\sigma a\left [ \fracz^33 \right ]_\frac-b2^\fracb2=\frac112\sigma ab^3$

Sekarang ketumpatan jisim permukaan σ digantikan oleh:

σ = m/ab

Dan ia pasti seperti ini:

$I=\frac112\sigma ab^3=\frac112\left ( \fracMab \right )ab^3=\frac112Mb^2$

Perhatikan bahawa ia seperti bar nipis.

Momen inersia lembaran persegi berkenaan dengan paksi yang melewati pusatnya

Untuk satu persegi di sebelah L, Dalam ungkapan sebelumnya yang sah untuk segi empat tepat, nilai b oleh yang satu L:

$I=\frac112ML^2$

Teorema Momen Inersia

Terdapat dua teorema yang sangat berguna untuk memudahkan pengiraan momen inersia berkenaan dengan paksi lain, yang sebaliknya boleh menjadi rumit untuk mencari kekurangan simetri. Teorema ini adalah:

Teorem Steiner

Juga dipanggil Teorem paksi selari, mengaitkan momen inersia mengenai paksi dengan yang lain yang melewati pusat jisim objek, selagi paksi selari. Untuk memohonnya, jarak d perlu diketahui di antara kedua -dua paksi dan tentu saja jisim m objek.

Menjadi Yo_zsaat inersia objek lanjutan berkenaan dengan Z, saya paksi_CmMomen inersia berkenaan dengan paksi yang melewati Pusat Massa (cm) objek tersebut, maka ia dipenuhi bahawa:

Yo_z = I_Cm + Md²

Atau dalam notasi angka berikut: Yo_{z '} = I_z + Md²

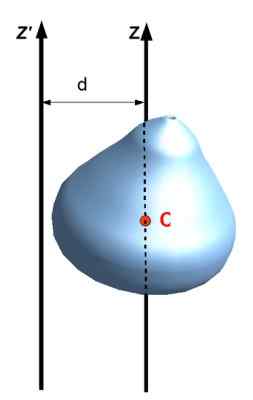Rajah 8. Teorem Steiner atau paksi selari. Sumber: Wikimedia Commons. Jack Lihat [CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Teorem paksi tegak lurus

Teorem ini digunakan untuk permukaan rata dan berkata: Momen inersia objek rata di sekitar paksi serenjang padanya adalah jumlah momen inersia sekitar dua paksi serenjang dengan paksi pertama:

Yo_z = I_x + Yo_dan

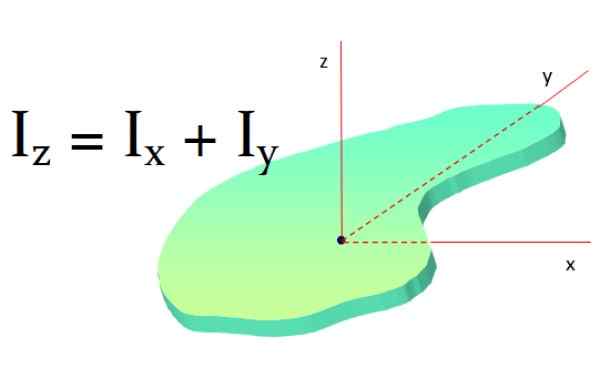Rajah 9. Teorem paksi tegak lurus. Sumber: f. Zapata.

Sekiranya objek mempunyai simetri seperti itu Yo_x dan Yo_dan Mereka sama, maka ia dipenuhi:

Yo_z = 2i_x

Latihan diselesaikan

Cari momen inersia bar berkenaan dengan paksi yang melewati salah satu hujungnya, seperti yang ditunjukkan dalam Rajah 1 (di bawah dan ke kanan) dan Rajah 10.

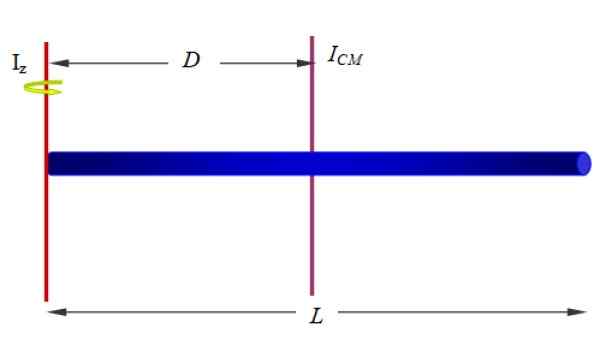Rajah 10. Momen inersia bar homogen di sekitar paksi yang melewati satu hujung. Sumber: f. Zapata.

Penyelesaian:

Kami sudah mempunyai momen inersia bar di sekitar paksi yang melalui pusat geometri. Oleh kerana bar adalah homogen, pusat jisimnya pada ketika itu, jadi ini akan menjadi milik kita Yo_Cm Untuk memohon Teorem Steiner.

Sekiranya panjang bar adalah L, Paksi z berada pada jarak d = l/2, oleh itu:

Yo_z = I_Cm + Md²= (1/12) ml²+M (l/2)²= (1/3) ml²

Rujukan

Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 313-340
Rex, a. 2011. Asas Fizik. Pearson. 190-200.
Teorem paksi selari. Pulih dari: Hyperphysics.Phy-Astr.GSU.Edu.
Serway, r. 2018. Fizik untuk Sains dan Kejuruteraan. Jilid 1. Cengage.
Sevilla University. Momen inersia pepejal sfera. Pulih dari: Laplace.kita.adalah.
Sevilla University. Momen inersia sistem zarah. Pulih dari: Laplace.kita.adalah.
Wikipedia. Teorem paksi selari. Diperoleh dari: dalam.Wikipedia.org