Pergerakan pekeliling seragam (m.C.Atau.) formula, ciri

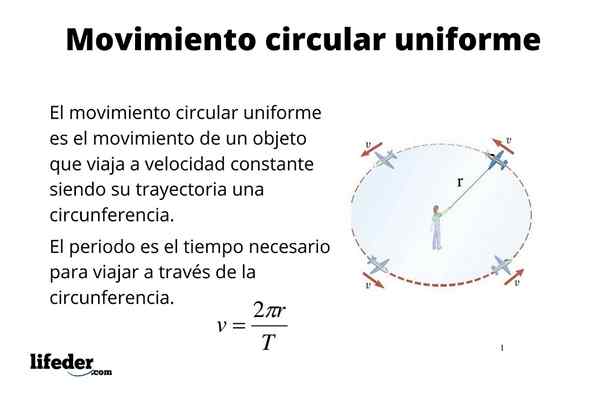
Zarah mempunyai Pergerakan bulat seragam (M.C.Atau.) Apabila trajektorinya adalah lilitan dan juga mengembara secara berterusan. Banyak objek seperti kepingan jentera dan enjin, misalnya, mempunyai pergerakan seperti ini, di antaranya cakera keras komputer, fenater, paksi dan banyak lagi perkara yang lebih banyak lagi.

Pergerakan bulat seragam juga merupakan pendekatan yang baik untuk pergerakan beberapa badan langit seperti Bumi. Orbit Bumi benar -benar elips, seperti yang ditunjukkan oleh undang -undang Kepler. Walau bagaimanapun, sifat eksentrik orbit adalah kecil dan sebagai pendekatan pertama ia dapat dianggap bulat, yang memudahkan beberapa pengiraan, seperti mencari kelajuan bumi ketika bergerak di sekitar matahari.

Dalam perihalan pergerakan pekeliling seragam, parameter yang sama digunakan seperti dalam pergerakan rectilinear, iaitu kedudukan, anjakan, masa, kelajuan dan percepatan.

Pecutan? Ya, sebenarnya, pergerakan pekeliling seragam dipercepatkan, walaupun kelajuannya v tetap malar. Ini kerana kelajuan v, Itu adalah vektor dan itulah sebabnya ia berani, ia terus mengubah arahnya sebagai objek atau zarah berputar. Sebarang perubahan dalam v Ia dihasilkan oleh pecutan, yang akan dilihat, diarahkan ke pusat trajektori bulat.

Pergerakan bulat seragam adalah pergerakan dalam pesawat Xy, Oleh itu ia adalah pergerakan dua dimensi. Walau bagaimanapun, adalah mungkin untuk menyatakannya dengan lebih selesa melalui sudut θ yang menyapu zarah, diukur berkenaan dengan paksi mendatar atau paksi rujukan lain yang sesuai.

Walaupun ia adalah objek yang dilanjutkan, zarahnya selalu menyapu sudut yang sama, walaupun mereka mempunyai koordinat yang berbeza (X, y).

[TOC]

Ciri -ciri pergerakan pekeliling seragam

Anda boleh meringkaskan ciri -ciri pergerakan pekeliling seragam seperti berikut:

-Trajektori adalah lilitan, oleh itu ia adalah pergerakan dalam pesawat.

-Kelajuan v Ia tetap, tetapi kelajuannya v Tidak, kerana ia terus mengubah arah dan makna untuk menampung giliran mudah alih.

-Vektor halaju v Selalunya tangen ke lilitan dan tegak lurus ke arah radial.

-Halaju sudut Ω adalah malar.

-Walaupun seragam, ada pecutan untuk menjelaskan perubahan ini ke arah kelajuan. Percepatan ini adalah pecutan sentripetal.

-Pecutan dan kelajuan sentripetal berserenjang antara satu sama lain.

-Ia adalah pergerakan berkala atau berulang, oleh itu tempoh magnitud dan kekerapan ditakrifkan untuknya.

Formula Pergerakan Pekeliling Seragam

Dalam skim ini terdapat putaran z zarah v ditarik.

Boleh melayani anda: medan magnet bumi: asal, ciri, fungsi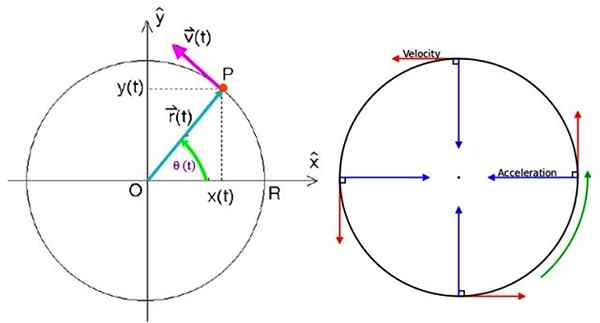 Parameter Pergerakan Pekeliling Seragam. Sumber: f. Zapata/Wikimedia Commons.

Untuk menentukan vektor kedudukan, perlu.

Vektor kedudukan

Ia dilambangkan sebagai r (t) dan diarahkan dari asal ke titik p di mana zarah terletak. Dalam T -segera yang diberikan t, dalam koordinat Cartesian, ia ditulis sebagai:

r (t) = x (t) Yo + dan (t) J

Di mana Yo dan J Mereka adalah vektor unit tegak lurus ke arah x dan dan masing -masing. Grafik diperhatikan bahawa modul vektor r (t) Sentiasa baik -baik saja R, Jejari lilitan. Sekiranya θ adalah sudut yang membentuk r Dengan paksi mendatar, kedudukannya juga sama:

r (t) = [RCOS θ(t)] Yo +[Rsen θ(t)] J

Sudut yang terbentuk r (T) Dengan paksi mendatar ia adalah sudut pusat dan nilainya adalah:

θ = s/r

Di mana s adalah arka lilitan yang dilalui dan radio. Sudut berkata θ Ia adalah fungsi masa, jadi anda boleh menulis θ = θ (T), Panggilan kedudukan sudut.

Oleh kerana kelajuan adalah malar, zarah menggambarkan sudut yang sama dalam masa yang sama dan dalam analogi dengan pergerakan rectilinear seragam, ditulis:

θ = θ (t) = θ_{Sama ada} + ωt

Di sini θ_{Sama ada} Ia adalah sudut awal yang diukur dalam radian berkenaan dengan paksi rujukan, ia boleh menjadi 0 atau sebarang nilai dan Ω adalah kelajuan sudut.

Kelajuan sudut dan kelajuan linear

Halaju sudut adalah yang pertama yang diperoleh dari kedudukan sudut dan dilambangkan sebagai Ω. Nilainya adalah malar untuk pergerakan pekeliling seragam, kerana sudut yang sama adalah pagar pada masa yang sama. Dalam kata lain:

Halaju sudut datang dalam unit radian/s. Bagi bahagiannya, kelajuan linear dikira oleh:

Kelajuan linear adalah modul atau magnitud kelajuan linear, yang berubah apabila zarah bertukar berikutan trajektorinya. Arah laju adalah alamat tangen ke lilitan.

Unit kelajuan linear dalam pergerakan pekeliling seragam adalah sama seperti pergerakan linear: m/s (dalam sistem antarabangsa SI), km/h, cm/s dan lain -lain.

Pecutan centripetal

Dalam angka berikut terdapat zarah yang bergerak dalam jadual lilitan dengan kelajuan malar. Ini bermaksud bahawa vektor kelajuan mempunyai modul yang sama selalu, tetapi mengubah arah untuk menampung lilitan.

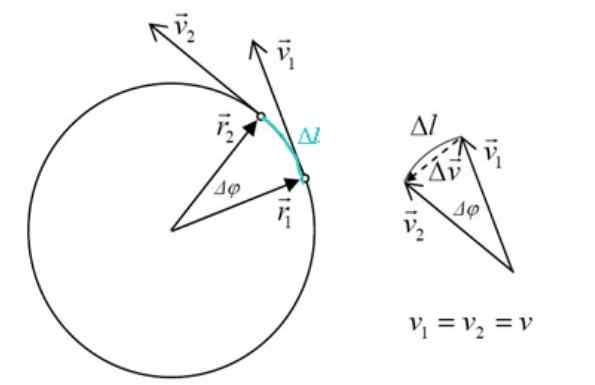Kelajuan dan pecutan dalam pergerakan pekeliling seragam. Sumber: f. Zapata.

Sebarang perubahan hasil kelajuan ke pecutan, yang mengikut definisi adalah:

Boleh melayani anda: 31 jenis daya dalam fizik dan ciri mereka

Dalam imej di atas adalah penolakan di antara vektor v₂ dan v₁, hasilnya adalah δv, vektor berkadar dengan pecutan. Seperti yang anda lihat, selalu menunjuk ke pusat lilitan dan itulah sebabnya ia dipanggil percepatan sentripetal atau pecutan radial.

Segitiga yang dibentuk oleh v₂, v₁ dan δv Ia serupa dengan segitiga sisi r₂, r₁ dan δL, Menjadi Δφ sudut pusat. Magnitud r₂ dan r₁ Mereka sama, jadi:

r₂ = r₁ = r

Kemudian, kedua -dua segitiga adalah hubungan ini untuk sudut:

Δφ = ΔR / r; Δφ = Δv / v

Bold tidak perlu, kerana ukuran sudut bergantung pada magnitud vektor ini. Menyamakan ungkapan di atas yang berikut:

 Jadi:

Membahagikan kedua -dua belah pihak dengan ΔT, untuk mendapatkan magnitud pecutan:

Tetapi ΔR / ΔT adalah magnitud kelajuan, yang dipanggil v, Oleh itu:

Akhirnya pecutan sentripetal adalah:

Tempoh dan kekerapan

Oleh kerana pergerakan bulat berulang, tempoh ditakrifkan T sama seperti masa yang diperlukan untuk mudah alih untuk mengambil giliran lengkap. Oleh kerana panjang jejari jejari r adalah 2πr, sudut yang disapu dalam radian apabila beralih lengkap adalah 2π radians dan mengambil masa t, halaju sudut adalah:

Ω = 2π / t

T = 2π / Ω

Tempoh pergerakan pekeliling seragam diukur dalam beberapa saat dalam sistem antarabangsa.

Bagi bahagiannya, kekerapan F Ia adalah bilangan giliran per unit masa dan adalah timbal balik atau terbalik dalam tempoh:

F = n /t = 1 /t

Unit kekerapan dalam sistem antarabangsa adalah s^-1.

Contoh Pergerakan Pekeliling Seragam

Ramai objek berputar untuk menghasilkan pelbagai kesan: roda, cakera dan turbin. Sebaik sahaja kelajuan operasi dicapai, putaran biasanya dilakukan dengan kelajuan yang berterusan. Pergerakan bulat sangat biasa dalam kehidupan seharian yang hampir tidak pernah anda fikirkan, jadi di sini terdapat beberapa contoh dekat yang menggambarkannya dengan baik:

Pergerakan bumi

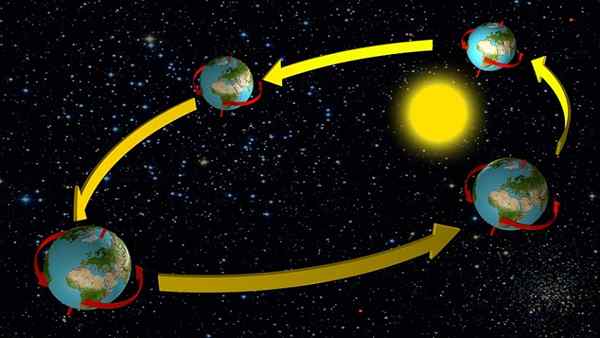
Bumi dan planet lain sistem suria bergerak dalam trajektori elips eksentrik kecil, kecuali merkuri, yang bermaksud bahawa dalam pendekatan pertama, dapat diandaikan bahawa pergerakannya adalah seragam pekeliling.

Ini mempunyai idea yang baik tentang kelajuan terjemahan di sekitar matahari, kerana dalam kes bumi, tempoh pergerakan diketahui: satu tahun atau 365 hari.

Zarah di pinggir album

Zarah -zarah yang berputar di pinggir toadiscos kuno atau fad kipas, ikuti pergerakan pekeliling seragam, apabila peranti mencapai kelajuan pembiakannya.

Boleh melayani anda: Model Atom Dirac Jordan: Ciri -ciri dan Postulates

Teleskop Angkasa Hubble

Teleskop Angkasa Hubble berputar di sekitar Bumi pada kira -kira 7550 m/s.

Centrifugators

Mesin basuh menjalankan proses sentrifugasi untuk memerah pakaian, yang terdiri daripada berputar drum kontena berkelajuan tinggi. Pengering juga beralih untuk tempoh masa dengan pergerakan pekeliling seragam.

Sentrifugasi juga digunakan di makmal untuk memisahkan sebatian, contohnya, dan dengan itu memisahkan pengundi dengan perbezaan kepadatan. Setiap kali ada perbincangan mengenai sentrifugasi, terdapat pergerakan bulat yang seragam, sekurang -kurangnya untuk seketika.

Hujan taman

Banyak hujan taman terus beralih ke tanah ke air dalam pasangan.

Sukan

Dalam pelancaran Hammer sebagai contoh, yang merupakan disiplin Olimpik, atlet bertukar bola logam dengan kabel keluli yang dilampirkan pada pemegangnya. Matlamatnya adalah untuk menghantar bola sejauh mungkin, tetapi tanpa meninggalkan kawasan tertentu.

Latihan diselesaikan

Zarah bergerak dalam lingkaran radius 2m dengan kelajuan tetap v = 8 m/s, ke arah yang bertentangan dengan jam. Pada mulanya zarah berada di r = +2 J m. Kira:

a) halaju sudut Ω

b) Kedudukan sudutnya θ (t)

c) tempoh pergerakan

d) pecutan sentripetal.

e) Kedudukan zarah selepas lulus t = π/4 s

Penyelesaian kepada

Dari formula v = rΩ ia mengikutinya:

Ω = v/r = (8 m/s)/2m = 4rad ∙ s^-1

Penyelesaian b

Mengambil sebagai paksi rujukan kepada paksi x positif, zarah pada mulanya pada 90º = π/2 radians berkenaan dengan paksi tersebut, kerana kenyataan itu mengatakan bahawa kedudukan awal adalah +2 J m, iaitu, zarah berada dalam y = 2m apabila pergerakan mula mengikuti.

θ = θ (t) = θ_{Sama ada} + ωt = π/2 + 4t

Penyelesaian c

T = 2π / Ω = 2π / 4 s = 0.5 π s

Penyelesaian d

a = v² / R = (8 m/ s)² / 2 m = 32 m/ s²

Penyelesaian e

θ (t) = π/2 + 4t → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 radians

Ini bermakna bahawa selepas masa itu, zarah berada dalam kedudukan y = -2m J. Ia masuk akal kerana t = π/4 s adalah separuh daripada tempoh, oleh itu zarah melawat sudut 180º dalam pengertian anti -horary sejak kedudukan awalnya dan harus berada di kedudukan yang bertentangan.

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
2. GiMbattista, a. 2010. Fizik. 2. Ed. McGraw Hill.
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.
5. Zapata, f. Pergerakan bulat. Pulih dari: Francesphysics.Blogspot.com.