Pergerakan Pendular

Apa itu Gerakan Pendular?

Dia Pergerakan Pendular Ini adalah pergerakan berayun yang dibuat oleh objek yang lebih berat, yang dipanggil pendulum, digantung oleh tali atau batang cahaya, ditetapkan pada ujungnya yang lain.

Pendulum diberikan dorongan awal dan dibenarkan untuk berayun, dengan cara ini objek menggambarkan gerbang perjalanan bulat. Inilah prinsip operasi jam tangan pendulum, buaian, kerusi goyang dan Metronom pendulum, digunakan untuk menandakan masa dalam muzik.

Pendulum berayun, menunjukkan kelajuan dan pecutan (Wikipedia.org)

Dikatakan bahawa menjelang 1581, Galileo Galilei memerhatikan pengaruh lampu di katedral Pisa, memerhatikan bahawa, walaupun amplitud osilasi lilin berkurangan kerana geseran dengan udara, bukan tempoh tempoh tempoh tersebut dari tempoh kitaran.

Ini menarik perhatian Galileo, yang memutuskan untuk meneruskan kajian dan menentukan bahawa tempoh pendulum tidak bergantung pada doh, tetapi pada akar kuadrat panjang tali, seperti yang akan dilihat kemudian.

Ciri -ciri pergerakan pendulih

Pendulum sangat mudah dibina, kerana sudah cukup dengan plumb gantung benang kapas dan memegang di ujung yang lain dengan jari anda atau dengan mengikatnya dengan sokongan seperti kuku.

Selepas dorongan awal yang kecil, berat badan bertanggungjawab untuk menjaga pendulum berayun, walaupun geseran mengurangkan amplitud pergerakan, sehingga akhirnya terhenti.

Ciri utama pergerakan pendulih adalah berulang -ulang, kerana ia adalah pergerakan sway. Sekarang, untuk memudahkan kajian anda, mudah untuk membuat beberapa penyederhanaan untuk memberi tumpuan kepada model yang lebih mudah, yang disebut Pendulum mudah.

Pendulum mudah

Kanak -kanak di ayunan boleh dimodelkan sebagai pendulum sederhana

Ia adalah sistem yang ideal yang terdiri daripada plumb, dianggap sebagai jisim tepat waktu m, tertakluk kepada tali panjang dan tidak dapat diteliti L. Ciri -ciri sistem ini adalah:

• Mempunyai pergerakan berulang dan berkala, yang terdiri daripada berulang -alik arka lilitan radius sama dengan l.
• Tidak mengambil kira geseran.
• Amplitud pergerakannya kecil (< 5º).
• Tempohnya bebas daripada jisim m, Dan ia hanya bergantung pada panjang L daripada pendulum.

Boleh melayani anda: vektor yang dihasilkan: pengiraan, contoh, latihan

Formula dan persamaan

Berikut adalah gambarajah pendulum yang mudah, di mana dua daya bertindak: berat badan P magnitud mg, yang diarahkan secara menegak dan ketegangan T Pada tali. Mereka tidak dianggap geseran.

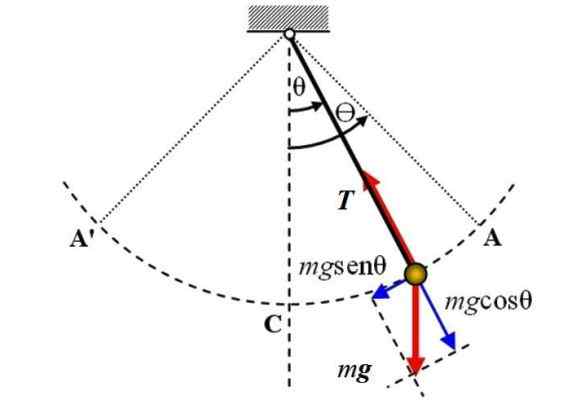Rajah badan percuma pendulum sederhana. Sumber: Wikimedia Commons.

Paksi rujukan adalah paksi menegak dan bertepatan dengan kedudukan θ = 0, dari sana anjakan sudut θ diukur, sama ada dalam satu arah atau yang lain. Tanda + boleh diberikan ke kanan dalam angka.

Untuk mengkaji pergerakan pendulum, sistem koordinat dipilih dengan asal dalam pendulum itu sendiri. Sistem ini mempunyai koordinat tangen ke arka lilitan a'ca yang diterangkan oleh pendulum, serta koordinat radial, yang diarahkan ke pusat trajektori.

Pada masa ini ditunjukkan dalam angka itu, pendulum bergerak ke kanan, tetapi komponen tangen graviti, yang dipanggil f_t, bertanggungjawab untuk membuatnya kembali. Diberi amaran tentang angka bahawa komponen ini membuat rasa bertentangan dengan pergerakan.

Bagi ketegangan pada tali, ia seimbang dengan komponen berat mgcosθ.

Kekuatan bersih, maka, yang dipanggil f_t Dan oleh undang -undang kedua Newton ia sama dengan produk Massa × pecutan, Dan ini seterusnya adalah yang kedua diperoleh dari anjakan linear s, Apa arka yang dilalui oleh pendulum. Jadi:

Anjakan sudut 

Persamaan mesti dinyatakan dari segi pembolehubah tunggal, mengingati bahawa anjakan sudut θ dan gerbang yang dilalui berkaitan dengan persamaan:

Ia boleh melayani anda: Undang -undang Termodinamik Kedua: Formula, Persamaan, Contoh

s = l.θ

Jisim dibatalkan di kedua -dua belah pihak dan jika amplitud kecil, sudut θ juga, dengan cara pendekatan berikut adalah sah:

dosa θ ≈ θ

Dengan ini, persamaan pembezaan berikut untuk pembolehubah θ (t) diperoleh:

Persamaan ini sangat mudah diselesaikan, kerana penyelesaiannya adalah fungsi yang derivatif kedua adalah fungsi itu sendiri. Terdapat tiga alternatif: kosinus, satu payudara atau eksponen. Fungsi kosinus dipilih untuk anjakan sudut θ (t), kerana ia adalah fungsi yang terkenal dan mudah dikendalikan.

Pembaca boleh menyemak, memperoleh dua kali, bahawa fungsi berikut memenuhi persamaan pembezaan:

θ (t) = θ_m cos (ωt + φ)

Di mana θ_m Ia adalah sudut maksimum bahawa pendulum bergerak dengan kekerapan menegak dan sudut Ω adalah:

Pemalar φ ditambah untuk memberikan keluasan kepada penyelesaian dan sesuai dengan keadaan awal.

Persamaan Tempoh

Tempoh T pergerakan adalah masa yang diperlukan untuk melaksanakan kitaran dan ditakrifkan sebagai:

Menggantikan Ω:

Seperti yang telah ditetapkan sebelum ini, tempoh itu tidak bergantung kepada jisim pendulum, tetapi hanya pada panjangnya.

Contoh pergerakan pendulih

Ukuran kadar jantung

Galileo mempunyai berlakunya mengukur kadar jantung orang, menyesuaikan panjang pendulum sehingga tempoh dengan denyutan jantung seseorang bertepatan.

Jam Pendulum

Ini sudah pasti salah satu contoh pergerakan pendulih yang paling biasa. Pembuatan jam tangan pendulum mempunyai sains dan seni. Fizik Belanda Christian Huygens (1629-1695) mengembangkan jam tangan pendulum pertama pada tahun 1656, berdasarkan kajian yang dibuat tahun lalu oleh Galileo.

Boleh melayani anda: optik bergelora

Pendulum Foucault

Pendulum Foucault. Sumber: Wikimedia Commons.

Ia adalah pendulum yang agak berbeza daripada yang diterangkan di atas, kerana ia mampu beralih ke mana -mana satah menegak. Ia dicipta oleh ahli fizik Perancis Léon Foucault (1819-1868) dan digunakan untuk menggambarkan putaran bumi.

Latihan diselesaikan

Pendulum mudah berlalu setiap 0.5 s untuk kedudukan keseimbangan. Berapakah panjang benang?

Penyelesaian

Oleh kerana tempoh adalah masa yang diperlukan untuk membuat kitaran lengkap, di mana ia berlalu dua kali melalui kedudukan keseimbangan: satu yang pertama dan yang lain kembali, kemudian:

T = 2 × 0.5 s = 1 s

Dari:

Panjang l benang dibersihkan:

Benang berukuran 0.Panjang 25 m atau 25 cm.

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 2. Dinamik. Diedit oleh Douglas Figueroa (USB).
2. GiMbattista, a. 2010. Fizik. 2. Ed. McGraw Hill.
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
4. Katz, d. 2013. Fizik untuk saintis dan jurutera. Asas dan sambungan. Pembelajaran Cengage.
5. Knight, r.  2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi.  Pearson.