Kaedah euler untuk apa penggunaan prosedur dan latihan

Dia Kaedah Euler Ini adalah prosedur yang paling asas dan mudah yang digunakan untuk mencari penyelesaian angka anggaran, kepada persamaan pembezaan biasa perintah pertama, dengan syarat keadaan awalnya diketahui.

Persamaan pembezaan biasa (EDO) adalah persamaan yang berkaitan dengan fungsi yang tidak diketahui pemboleh ubah bebas tunggal dengan derivatifnya.

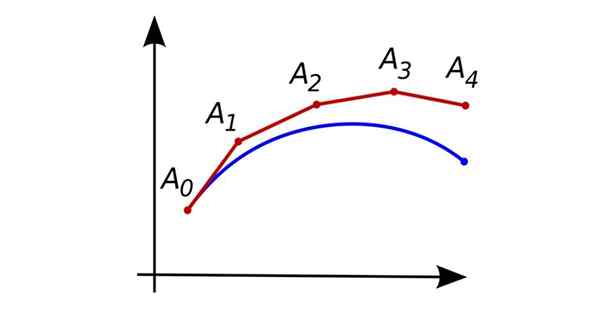
Pendekatan berturut -turut oleh kaedah Euler. Sumber: Oleg Alexandrov [Domain Awam]

Sekiranya derivatif terbesar yang muncul dalam persamaannya adalah ijazah, maka itu adalah persamaan pembezaan biasa pada tahap pertama.

Cara paling umum untuk menulis persamaan ijazah pertama ialah:

dengan keadaan awal:

x = x₀

y = y₀

[TOC]

Apakah kaedah Euler?

Idea kaedah Euler adalah untuk mencari penyelesaian berangka untuk persamaan pembezaan dalam selang antara x₀ dan x_F .

Pertama, selang dalam n+1 mata tidak bersetuju:

x₀, x₁, x₂, x₃..., x_n

Yang diperoleh seperti ini:
x_Yo= x₀+IH

Di mana h ialah lebar atau langkah subintervals:

Semakin besar bilangan n hasilnya akan lebih tepat, tetapi jumlah mata yang lebih besar diperlukan untuk menutup selang di mana kita mencari penyelesaian dan masa pengkomputeran tumbuh.

Dengan keadaan awal, maka juga mungkin untuk mengetahui derivatif pada mulanya:

dan '(x_{Sama ada}) = f (x_{Sama ada}, dan_{Sama ada})

Derivatif ini mewakili cerun garis tangen ke lengkung fungsi y (x) tepat pada titik:

Ao = (x_{Sama ada}, dan_{Sama ada})

Kemudian ramalan anggaran nilai fungsi y (x) dibuat pada titik berikut:

dan (x₁) ≈ dan₁

dan_1 = dan_{Sama ada} +(x₁- x_{Sama ada}) f (x_{Sama ada}, dan_{Sama ada}) = y_{Sama ada +} H f (x_{Sama ada}, dan_{Sama ada})

Titik anggaran seterusnya penyelesaian yang sesuai dengan:

Ke₁ = (x₁, dan₁)

Prosedur ini diulang untuk mendapatkan mata berturut -turut

Boleh melayani anda: Fungsi logaritma: sifat, contoh, latihan

Ke₂, Ke₃..., x_n

Dalam angka yang ditunjukkan pada mulanya, lengkung biru mewakili penyelesaian tepat persamaan pembezaan, dan yang merah mewakili titik anggaran berturut -turut yang diperolehi oleh prosedur Euler.

Latihan yang diselesaikan

Latihan 1

Yo) Menjadi persamaan pembezaan:

Dengan keadaan awal x = a = 0; dan_ke= 1

Dengan menggunakan kaedah Euler, dapatkan penyelesaian anggaran dan Dalam koordinat x = b = 0.5, membahagikan selang [a, b] pada n = 5 bahagian.

Penyelesaian

Hasil berangka diringkaskan seperti berikut:

Di mana disimpulkan bahawa penyelesaian dan nilai 0.5 adalah 1.4851.

Nota: Untuk merealisasikan pengiraan yang telah digunakan Smath Studio, Program Penggunaan Percuma Percuma.

Latihan 2

Ii) Meneruskan persamaan pembezaan Latihan I), cari penyelesaian yang tepat dan bandingkan dengan hasil yang diperolehi oleh kaedah Euler. Cari ralat atau perbezaan antara hasil yang tepat dan anggaran.

Penyelesaian

Dengan keadaan awal x = a = 0; dan_ke= 1
Penyelesaian yang tepat tidak begitu sukar dicari. Diketahui bahawa derivatif fungsi sen (x) adalah fungsi cos (x). Oleh itu penyelesaian y (x) akan menjadi:

dan (x) = sin x + c

Untuk memenuhi syarat awal dan (0) = 1, c tetap mesti bernilai 1. Seterusnya, hasil yang tepat dibandingkan dengan anggaran:

Disimpulkan bahawa dalam selang yang dikira, pendekatan ini mempunyai tiga angka ketepatan yang signifikan.

Latihan 3

Iii) Pertimbangkan persamaan pembezaan dan keadaan awalnya yang diberikan di bawah:

dan '(x) =- y²

Dengan keadaan awal x₀ = 0; dan₀ = 1

Gunakan kaedah Euler untuk mencari nilai anggaran penyelesaian dan (x) Dalam selang waktu x = [0, 1.5]. Gunakan langkah H = 0.1.

Penyelesaian

Kaedah Euler sangat ditunjukkan untuk digunakan dengan spreadsheet. Dalam kes ini kita akan menggunakan spreadsheet Geogebra, Program penggunaan percuma dan percuma.

Ia boleh melayani anda: Kompaun berkadar: Penjelasan, tiga peraturan kompaun, latihan

Tiga lajur (a, b, c) ditunjukkan dalam spreadsheet angka x , Lajur kedua mewakili pemboleh ubah dan, dan lajur ketiga terbitan dan '.

Baris 2 mengandungi nilai awal dari X, Dan, Dan ' .

Nilai nilai 0.1 Ia telah diletakkan di sel kedudukan mutlak ($ ​​d $ 4).

Nilai Y0 awal berada dalam sel B2, dan Y1 dalam sel B3. Untuk mengira dan₁ Formula digunakan:

dan_1 = dan_{Sama ada} +(x₁- x_{Sama ada}) f (x_{Sama ada}, dan_{Sama ada}) = y_{Sama ada +} H f (x_{Sama ada}, dan_{Sama ada})

Formula spreadsheet ini akan menjadi nombor b3: = b2 + $ d $ 4 * c3.

Begitu juga Y2 akan berada dalam sel B4 dan formulanya ditunjukkan dalam angka berikut:

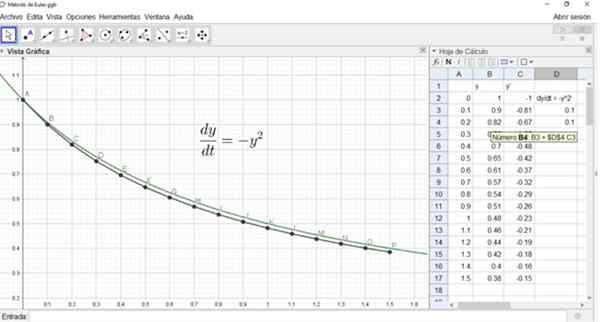
Angka ini juga menunjukkan graf penyelesaian yang tepat, dan titik a, b, ..., p penyelesaian anggaran dengan kaedah euler.

Kaedah Newton Dynamics dan Euler

Dinamika Klasik telah dibangunkan oleh Isaac Newton (1643 - 1727). Motivasi asal Leonard Euler (1707 - 1783) untuk membangunkan kaedahnya adalah tepat untuk menyelesaikan persamaan undang -undang kedua Newton dalam pelbagai situasi fizikal.

Undang -undang kedua Newton sering dinyatakan sebagai persamaan pembezaan sekunder:

Di mana x mewakili kedudukan objek pada masa ini t. Objek ini mempunyai jisim m dan tertakluk kepada kekuatan F. Fungsinya F Ia berkaitan dengan kekuatan dan jisim seperti berikut:

 Walaupun kaedah Euler pada prinsipnya direka untuk menyelesaikan persamaan pembezaan pertama, ia mudah diperpanjang kepada kes kedua, kerana ia bersamaan dengan sistem dua persamaan pertama.

Ia dapat melayani anda: geometri analisis

Untuk menggunakan kaedah Euler, nilai masa awal diperlukan t, kelajuan v dan kedudukan x.

Jadual berikut menerangkan bagaimana bermula dari nilai awal T1, V1, X1 Penghampiran kelajuan V2 dan kedudukan X2 boleh diperolehi, pada masa ini T2 = T1+ΔT, di mana ΔT mewakili peningkatan kecil dan sepadan dengan langkah Dalam kaedah Euler.

Latihan 4

Iv) Salah satu masalah asas dalam mekanik ialah blok jisim m yang terikat pada musim bunga (atau musim bunga) dari elastik malar k.

Undang -undang kedua Newton untuk masalah ini akan menjadi seperti ini:

Dalam contoh ini, untuk memudahkan ia akan diambil m = 1 dan k = 1. Cari penyelesaian anggaran ke kedudukan x Dan kelajuan v Oleh kaedah Euler dalam selang waktu [0, π/2] membahagikan selang dalam 12 bahagian.

Ambil 0 sebagai momen awal, kelajuan awal 0 dan kedudukan awal 1.

Penyelesaian

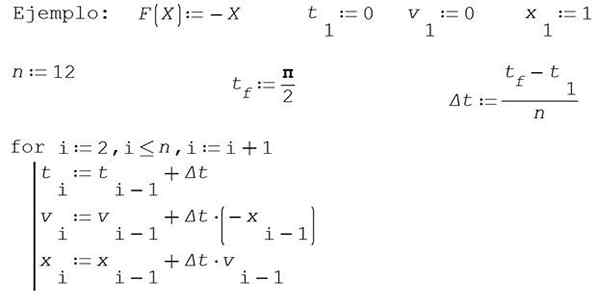
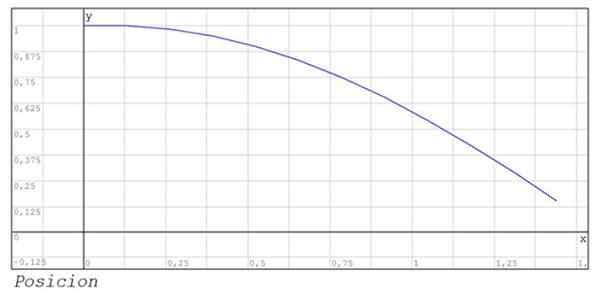
Hasil berangka ditunjukkan dalam jadual berikut:

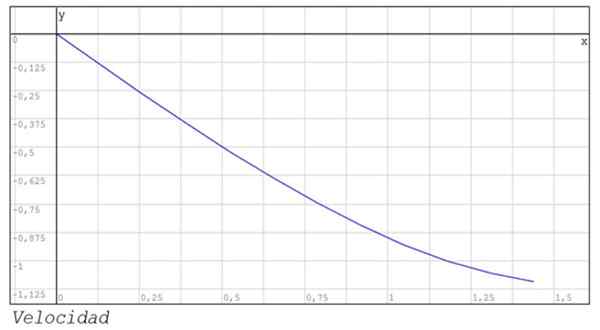
Grafik kedudukan dan kelajuan antara instan 0 dan 1 juga ditunjukkan.44.

Latihan yang dicadangkan untuk rumah

Latihan 1

Gunakan spreadsheet untuk menentukan penyelesaian anggaran menggunakan kaedah Euler untuk persamaan pembezaan:

dan '= -exp (-y) dengan keadaan awal x = 0, y = -1 dalam selang x = [0, 1]

Mulakan dengan langkah 0.1. Graf hasilnya.

Latihan 2

Dengan menggunakan spreadsheet, cari penyelesaian berangka ke persamaan ijazah kedua berikut, di mana dan ia adalah fungsi pembolehubah bebas t.

dan "= - 1/y² dengan keadaan awal t = 0; y (0) = 0.5; dan '(0) = 0

Cari penyelesaian dalam selang [0.5; 1.0] menggunakan langkah 0.05.

Graf hasilnya: dan vs t; dan 'vs t

Rujukan

1. Kaedah Eurler.Diambil dari Wikipedia.org
2. Solver Euler. Diambil daripada.Smath.com