Kaedah Hungary Apa yang terdiri, contohnya

Dia Kaedah Hungary Ini adalah algoritma yang digunakan dalam masalah peruntukan apabila anda ingin meminimumkan kos. Iaitu, ia digunakan untuk mencari kos minimum dengan memberikan beberapa orang kepada pelbagai aktiviti berdasarkan kos terendah. Setiap aktiviti mesti diberikan kepada orang yang berbeza.

Masalah tugasan adalah jenis masalah pengaturcaraan linear khas, di mana objektifnya adalah untuk meminimumkan kos atau masa menyelesaikan sejumlah kerja oleh beberapa orang.

Sumber: Pixabay.com

Salah satu ciri penting masalah peruntukan ialah hanya satu kerja (atau pekerja) yang diberikan kepada mesin (atau projek).

Kaedah ini dibangunkan oleh ahli matematik Hungary d. Konig. Atas sebab ini, ia dikenali sebagai kaedah Hungary untuk masalah peruntukan. Ia juga dikenali sebagai Algoritma Tugasan Kuhn-Munkres.

Sebarang masalah peruntukan dapat diselesaikan dengan mudah dengan menggunakan kaedah ini yang terdiri daripada dua fasa:

- Dengan fasa pertama terdapat pengurangan baris dan pengurangan lajur.

- Pada fasa kedua penyelesaian pada asas berulang dioptimumkan.

[TOC]

Apakah kaedah Hungary?

Kaedah Hungary terdiri daripada empat langkah. Dua langkah pertama dilaksanakan sekali sahaja, sementara langkah 3 dan 4 diulangi sehingga mereka mendapat tugasan yang optimum.

Ia dianggap sebagai fakta kemasukan ke matriks persegi perintah n oleh n, yang mesti mengandungi hanya unsur -unsur yang tidak negatif.

Untuk masalah yang diberikan, jika bilangan baris dalam matriks tidak sama dengan bilangan lajur baris fiktif atau lajur fiktif mesti ditambah, bergantung pada kes itu. Kos tugasan untuk sel -sel rekaan ini sentiasa ditugaskan sebagai sifar.

Langkah 1: Kurangkan minimum setiap baris

Untuk setiap baris matriks, elemen dipilih dengan nilai terendah dan penolakan setiap elemen dalam baris itu.

Boleh melayani anda: Apakah aset semasa? (Dengan contoh)

Langkah 2: Kurangkan minimum setiap lajur

Begitu juga, elemen dengan nilai terendah dipilih untuk setiap lajur dan menolaknya dari setiap elemen dalam lajur tersebut.

Langkah 3: Tutup semua sifar dengan bilangan baris minimum

Semua sifar mesti dilindungi dalam matriks yang terhasil dari langkah 2 menggunakan bilangan minimum garis mendatar dan menegak, sama ada dengan baris atau lajur.

Sekiranya jumlah garis diperlukan untuk menutup semua sifar, yang sama dengan saiz n per n matriks, akan ada tugasan yang optimum antara sifar dan oleh itu algoritma berhenti.

Jika tidak, jika kurang garis diperlukan untuk menutup semua sifar dalam matriks, ia berterusan dengan langkah 4.

Langkah 4: Buat sifar tambahan

Unsur paling sedikit matriks (dipanggil k) dipilih yang tidak dilindungi oleh salah satu baris yang dibuat dalam langkah 3.

Nilai k dari semua elemen yang tidak dilindungi oleh garis ditolak. Seterusnya, nilai k ditambah kepada semua unsur yang diliputi oleh persimpangan dua baris.

Unsur -unsur yang diliputi oleh satu baris tersisa seperti yang mereka ada. Setelah melakukan langkah ini, anda kembali ke Langkah 3.

Tugasan optimum

Sebaik sahaja algoritma dihentikan pada langkah 3, satu set sifar dipilih supaya setiap baris dan setiap lajur hanya mempunyai satu sifar yang dipilih.

Sekiranya dalam proses pemilihan ini tidak ada sifar tunggal dalam satu baris atau lajur, salah satu daripada sifar itu akan dipilih. Nol yang tersisa dihapuskan dalam lajur atau baris, mengulangi yang sama untuk tugasan lain juga.

Ia dapat melayani anda: makrolokalisasi

Sekiranya tidak ada satu peruntukan sifar bermakna terdapat banyak penyelesaian. Walau bagaimanapun, kos akan tetap sama untuk set peruntukan yang berbeza.

Sebarang baris atau lajur fiktif yang telah ditambah dihapuskan. Zeros yang dipilih dalam matriks terakhir ini sesuai dengan tugasan ideal yang diperlukan dalam matriks asal.

Contoh

Pertimbangkan sebuah syarikat di mana terdapat empat aktiviti (A1, A2, A3, A4) yang mesti dilaksanakan oleh empat pekerja (T1, T2, T3, T4). Aktiviti setiap pekerja mesti diberikan.

Matriks berikut menunjukkan kos untuk memberikan pekerja tertentu kepada aktiviti tertentu. Objektif yang dijalankan adalah untuk meminimumkan jumlah kos tugas yang terdiri daripada empat aktiviti ini.

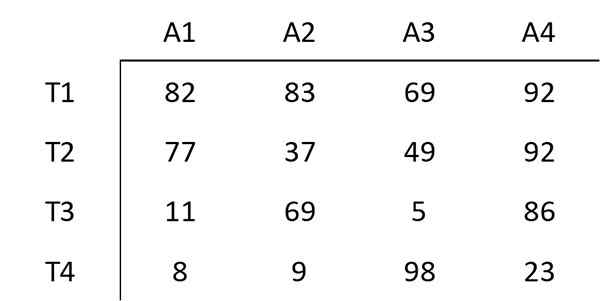
Langkah 1: Kurangkan minimum setiap baris

Unsur ini bermula dengan nilai minimum setiap baris unsur -unsur lain dari baris itu. Contohnya, elemen terkecil di baris pertama ialah 69. Oleh itu, 69 dari setiap elemen dikurangkan pada baris pertama. Matriks yang dihasilkan adalah:

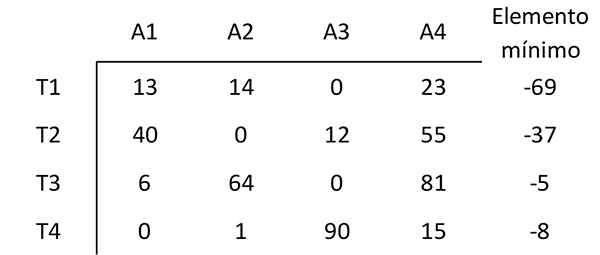
Langkah 2: Kurangkan minimum setiap lajur

Dengan cara yang sama, elemen dikurangkan dengan nilai minimum setiap lajur unsur -unsur lain dari lajur itu, memperoleh matriks berikut:

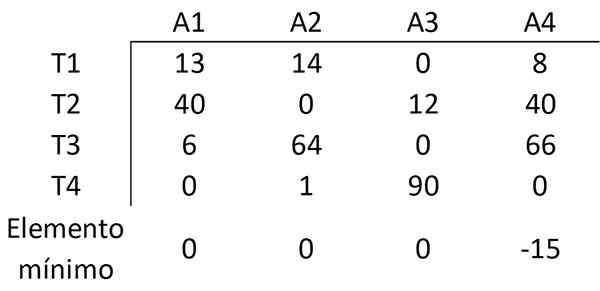
Langkah 3: Tutup semua sifar dengan bilangan baris minimum

Sekarang bilangan minimum baris (mendatar atau menegak) akan ditentukan yang diperlukan untuk menampung semua sifar dalam matriks. Semua nol boleh dilindungi menggunakan 3 baris:

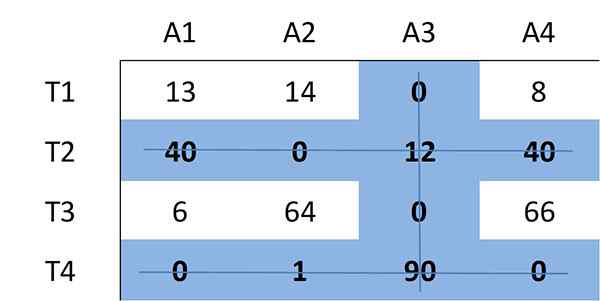
Kerana bilangan baris yang diperlukan adalah tiga dan kurang daripada saiz matriks (n = 4), ia berterusan dengan langkah 4.

Boleh melayani anda: Pengurusan Projek: Apakah, Fasa, Objektif, Contoh

Langkah 4: Buat sifar tambahan

Unsur terendah yang tidak dilindungi oleh garis dipilih, yang nilainya adalah 6. Nilai semua elemen yang tidak dicabut dikurangkan dan nilai yang sama ditambah kepada semua elemen yang diliputi oleh persimpangan dua baris. Ini menghasilkan matriks berikut:

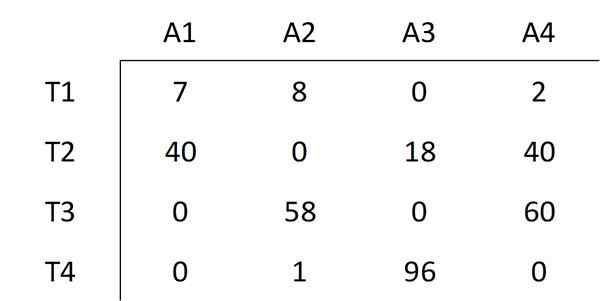
Seperti yang ditunjukkan dalam kaedah Hungary, langkah nombor tiga mesti dilakukan lagi.

Langkah 3 (pengulangan)

Sekali lagi bilangan minimum baris yang diperlukan untuk menampung semua sifar dalam matriks ditentukan. Kali ini empat baris diperlukan:

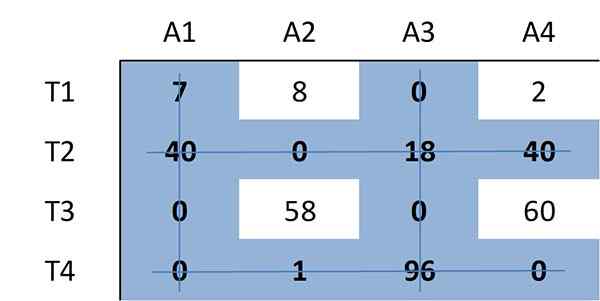
Kerana bilangan garis yang diperlukan adalah 4, sama dengan saiz matriks (n = 4), terdapat tugasan optimum antara sifar dalam matriks. Oleh itu, algoritma berhenti.

Tugasan optimum

Seperti yang ditunjukkan oleh kaedah, pemilihan yang diperbuat daripada sifar berikut sepadan dengan tugasan yang optimum:

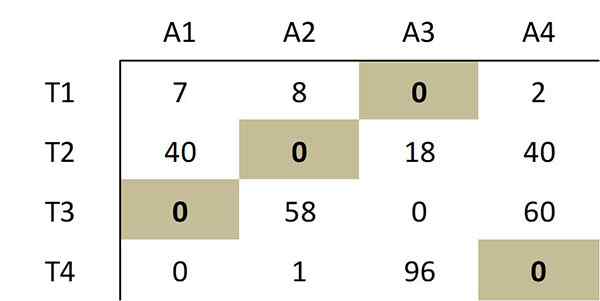
Pemilihan sifar ini sepadan dengan peruntukan optimum berikut dalam matriks kos asal:

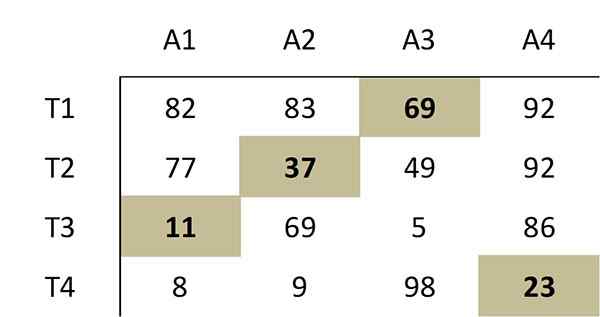
Oleh itu, Pekerja 1 mesti menjalankan Aktiviti 3, Pekerja 2, Aktiviti 2, Pekerja 3, Aktiviti 1 dan Pekerja 4 mesti menjalankan Aktiviti 4. Jumlah kos tugasan optimum ini ialah 69+37+11+23 = 140.

Rujukan

1. Algoritma Hungary (2019). Algoritma Hungary. Diambil dari: Hungarianalgoritma.com.
2. Kajian (2019). Menggunakan algoritma Hungary untuk menyelesaikan masalah tugasan. Diambil dari: Kajian.com.
3. Pekerjaan Kebijaksanaan (2018). Kaedah Hungary untuk menyelesaikan masalah tugasan - Teknik kuantitatif untuk pengurusan. Diambil dari: kebijaksanaan.com.
4. Geeks untuk Geeks (2019). Algoritma Hungary untuk masalah tugasan. Diambil dari: geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Algoritma Pencocokan Maksimum Hungary. Cemerlang. Diambil dari: cemerlang.org.