Nombor kuantum untuk apa gunanya dan apa itu

The nKuantum umeters Mereka digunakan untuk menggambarkan keadaan kuantum elektron dalam atom dan berasal dari penyelesaian persamaan Schrödinger untuk yang paling mudah semua: hidrogen.

Persamaan Schrödinger adalah persamaan pembezaan, yang penyelesaiannya Fungsi gelombang dan mereka dilambangkan oleh huruf Yunani ψ. Penyelesaian tak terhingga boleh dibangkitkan, dan perseginya bersamaan dengan kebarangkalian mencari elektron di kawasan kecil ruang, yang dipanggil orbital.

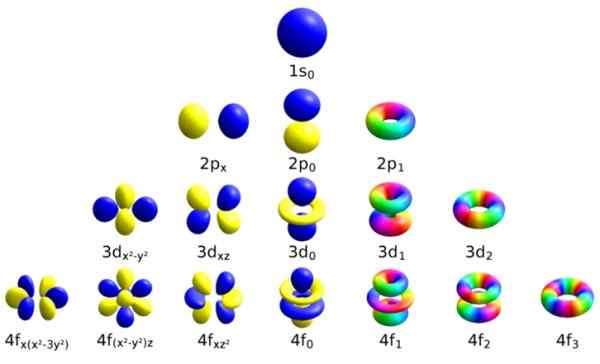
Setiap orbital atom ini dibezakan oleh set nombor kuantum tertentu. Sumber: Wikimedia Commons.

Setiap orbital telah menentukan ciri -ciri yang membezakannya dari orang lain, seperti tenaga, momentum sudut dan putaran, sifat kuantum sepenuhnya elektron dan yang bertanggungjawab, antara lain, untuk kesan magnet.

Cara untuk mengenal pasti setiap orbital adalah untuk membezakannya melalui satu set nombor yang menggambarkannya, dan ini adalah tepat nombor kuantum:

-N: Adakah nombor kuantum utama.

-ℓ: Nombor kuantum azimutal.

-m_ℓ, Ia adalah nombor magnet.

-m_s, Nombor putaran.

[TOC]

Apakah nombor kuantum?

Nombor kuantum berfungsi untuk menggambarkan keadaan elektron di dalam atom. Model atom di mana elektron bertukar di sekitar nukleus tidak tepat, kerana ia tidak konsisten dengan kestabilan atom atau dengan sejumlah besar fenomena fizikal yang diperhatikan.

Itulah sebabnya Denmark Niels Bohr (1885-1962) dibuat pada tahun 1913 cadangan yang berani: elektron hanya boleh didapati di orbit stabil tertentu, yang saiznya bergantung pada nombor integer yang dipanggil n.

Kemudian, pada tahun 1925, fizikal Austria Erwin Schrödinger (1887-1961) menimbulkan persamaan pembezaan dalam derivatif separa, yang penyelesaiannya menggambarkan atom hidrogen. Adakah fungsi gelombang ψ disebut pada awal.

Persamaan pembezaan ini termasuk tiga koordinat spatial ditambah masa, tetapi apabila tidak termasuk, penyelesaian persamaan Schrödinger adalah sama dengan gelombang pegun (gelombang yang merebak antara had tertentu).

Fungsi gelombang

Persamaan masa bebas Schrödinger diselesaikan dalam koordinat sfera dan penyelesaiannya ditulis sebagai produk dari tiga fungsi, satu untuk setiap pemboleh ubah spatial. Dalam sistem koordinat ini, bukannya menggunakan koordinat paksi Cartesian x, dan dan z koordinat digunakan r, θ dan φ. Cara ini:

Boleh melayani anda: litar selari

ψ (r, θ, φ) = r (r) ⋅f (θ) ⋅g (φ)

Fungsi gelombang tidak ketara, walaupun mekanik kuantum ia memberitahu kita bahawa amplitud persegi:

| ψ (r, θ, φ) |²

Iaitu, modul atau nilai mutlak fungsi gelombang, kuadrat, adalah nombor sebenar yang mewakili kebarangkalian mencari elektron, di rantau tertentu di sekitar titik yang koordinat r, θ dan φ.

Dan fakta ini adalah sesuatu yang lebih konkrit dan ketara.

Untuk mencari fungsi gelombang, anda perlu menyelesaikan tiga persamaan pembezaan biasa, satu untuk setiap pemboleh ubah r, θ dan φ.

Penyelesaian setiap persamaan, yang akan menjadi fungsi r (r), f (θ) dan g (φ), mengandungi tiga nombor kuantum pertama yang disebutkan.

Apakah nombor kuantum?

Di bawah kita secara ringkas menerangkan sifat setiap nombor kuantum. Tiga yang pertama, seperti yang dinyatakan di atas, timbul dari penyelesaian persamaan Schrödinger.

Nombor keempat ditambah oleh Paul Dirac (1902 - 1984) pada tahun 1928.

Nombor kuantum utama

Ia dilambangkan oleh n dan menunjukkan saiz orbital yang dibenarkan, serta tenaga elektron. Semakin tinggi nilainya, semakin banyak elektron nukleus dan tenaganya juga akan menjadi, tetapi sebagai balasannya ia mengurangkan kestabilannya.

Nombor ini timbul dari fungsi r (r), yang merupakan kebarangkalian mencari elektron pada jarak tertentu r daripada nukleus, yang ditentukan oleh:

 Di mana pemalar berikut mengambil bahagian:

-Pemalar Planck: H = 6,626 × 10 ^{-3. 4} J.s
-Jisim elektron m_dan = 9.1 × 10^-31 kg
-Beban elektron: E = 1.6 × 10^-19 C.
-Pemalar elektrostatik: k = 9 × 10 ⁹ N.m²/C²

Apabila n = 1 sepadan dengan jejari bohr yang bernilai kira -kira 5.3 × 10^-11 m.

Kecuali untuk lapisan pertama, yang lain dibahagikan kepada subcaps atau sub -level. Setiap lapisan mempunyai tenaga dalam elektron volt yang diberikan oleh:

Boleh melayani anda: Gelombang mekanikal: ciri, sifat, formula, jenis

Istilah EV "Volt Elektron" bermaksud, unit tenaga yang digunakan dengan kerap di kawasan fizik kuantum. Di mana n = 1, 2, 3, 4 .. . dan setiap nilai n sepadan dengan a lapisan, yang dilabelkan dengan huruf besar:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Atau (n = 5)
• P (n = 6)
• Q (n = 7).

Secara teori tidak ada had atas untuk n, tetapi dalam praktiknya diperhatikan bahawa ia hanya mencapai n = 8. Tenaga paling tidak mungkin sepadan dengan n = 1 dan adalah dari Keadaan asas.

Nombor kuantum azimutal atau momentum sudut

Dilambangkan oleh huruf italik, nombor ini menentukan bentuk orbital, apabila mengukur magnitud momentum sudut orbital elektron.

Anda boleh mengambil nilai keseluruhan dan positif antara 0 dan n-1, sebagai contoh:

-Apabila n = 1, maka ℓ = 0 dan terdapat satu sub -level.

-Jika n = 2, maka ℓ boleh bernilai 0 atau 1, jadi anda mempunyai dua sub -level.

-Dan jika n = 3, maka ℓ menganggap nilai 0, 1 dan 2 dan terdapat 3 sub -level.

Ia boleh diikuti selama -lamanya, walaupun seperti yang dinyatakan sebelum ini, dalam amalan n mencapai sehingga 8. Sub -level dilambangkan melalui huruf: s, p, d, F dan g Dan mereka semakin meningkat tenaga.

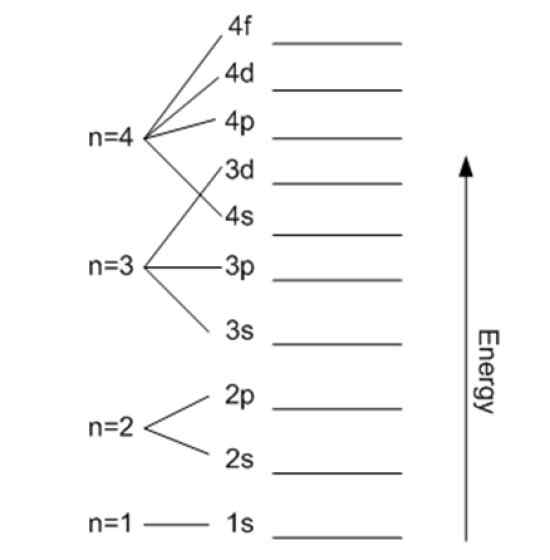Tenaga berkaitan dengan nombor kuantum utama. Sumber: Wikimedia Commons.

Nombor kuantum magnet m_ℓ

Nombor ini menentukan orientasi orbital di ruang angkasa dan nilainya bergantung pada ℓ.

Untuk ℓ yang diberikan, terdapat (2 ℓ+1) nilai keseluruhan m _ℓ, sepadan dengan orbital masing -masing. Ini adalah:

-ℓ, ( - ℓ+1), ... 0, ... (+ℓ -1),+ℓ.

Contoh

Jika n = 2, kita tahu bahawa ℓ = 0 dan ℓ = 1, maka m _ℓ Ambil nilai berikut:

-Untuk ℓ = 0: m _ℓ = 0.
-Untuk ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbital n = 2 mempunyai dua sub -level, yang pertama dengan n = 2, ℓ = 0 dan m _ℓ = 0. Kemudian kita mempunyai sub -level kedua: n = 2, ℓ = 1, dengan 3 orbital:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

Tiga orbital mempunyai tenaga yang sama tetapi orientasi spatial yang berbeza.

Bilangan kuantum spin m_s

Semasa menyelesaikan persamaan Schrödinger dalam tiga dimensi, nombor yang telah diterangkan timbul. Walau bagaimanapun, dalam hidrogen struktur lebih jauh diperhatikan daripada nombor -nombor ini tidak mencukupi untuk dijelaskan.

Ia boleh melayani anda: pemalar gas: apakah, pengiraan dan contoh

Oleh itu, pada tahun 1921 badan lain, Wolfgang Pauli, mencadangkan kewujudan nombor keempat: nombor putaran m_s, yang memerlukan nilai +½ atau -½.

Dengan nombor ini harta yang sangat penting dalam elektron diterangkan, iaitu berputar, Perkataan yang berasal dari bahasa Inggeris berputar (Hidupkan diri anda). Dan putaran pula berkaitan dengan sifat magnet atom.

Salah satu cara untuk memahami putaran adalah membayangkan bahawa elektron berkelakuan seperti dipole magnet kecil (magnet dengan tiang utara dan selatan), terima kasih kepada putaran di sekitar paksi sendiri. Giliran boleh berada dalam arah yang sama dengan jarum jam, atau ke arah yang bertentangan.

Walaupun Pauli mencadangkan kewujudan nombor ini, hasil percubaan yang dijalankan oleh Otto Stern dan Walter Gerlach pada tahun 1922 telah menjangkakannya.

Para saintis ini berjaya membahagikan rasuk atom perak dengan penerapan medan magnet yang tidak bersifat seragam.

Nilai m_s Ia tidak bergantung pada n, ℓ dan m _ℓ. Secara grafik, ia diwakili oleh anak panah: anak panah ke atas menunjukkan jadual dan satu di bawah antihoran.

Prinsip Pengecualian Pauli

Tingkah laku elektron dalam atom diringkaskan dalam prinsip pengecualian Pauli, yang menyatakan bahawa dua elektron atom tidak dapat wujud dalam keadaan kuantum yang sama.

Oleh itu, setiap elektron mesti mempunyai set bilangan kuantum yang berbeza n, ℓ, m _ℓ dan m_s.

Kepentingan nombor kuantum dan prinsip ini terletak pada pemahaman sifat-sifat unsur.

Rujukan

1. Alonso, m. 1971. Asas kuantum dan statistik. Dana Pendidikan Inter -American.
2. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
3. Chang, R. 2013. Kimia. 11va. Edisi. Pendidikan MC Graw Hill.
4. Eisberg-Resnick. 1989. Fizik kuantum. Limusa - Wiley.
5. GiMbattista, a. 2010. Fizik. 2. Ed. McGraw Hill.
6. Rex, a. 2011. Asas Fizik. Pearson.
7. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. McGraw Hill.