Nombor Irrational Nombor, sifat, klasifikasi, contoh

The nombor tidak rasional Mereka adalah orang -orang yang ekspresi perpuluhan mempunyai angka yang tidak terhingga tanpa corak berulang, oleh itu, mereka tidak dapat diperoleh dengan membuat kuota antara dua bilangan bulat.

Antara nombor tidak rasional yang paling terkenal ialah:

Rajah 1. Dari atas ke bawah nombor tidak rasional berikut: pi, bilangan euler, aúrea dan dua akar persegi. Sumber: Pixabay.

Antara mereka, tanpa keraguan π (pi) adalah yang paling biasa, tetapi ada banyak lagi. Semuanya tergolong dalam set nombor sebenar, yang merupakan set berangka yang menyatukan nombor rasional dan tidak rasional.

Titik yang menggembirakan dalam Rajah 1 menunjukkan bahawa perpuluhan mengikuti selama -lamanya, apa yang berlaku adalah bahawa ruang kalkulator semasa hanya membolehkan untuk menunjukkan beberapa.

Sekiranya kita melihat dengan teliti, dengan syarat kita membuat kuota antara dua bilangan bulat, perpuluhan dengan angka terhad diperoleh atau jika tidak, dengan angka tak terhingga di mana satu atau lebih mereka diulang. Nah, ini tidak berlaku dengan nombor yang tidak rasional.

[TOC]

Sejarah nombor yang tidak rasional

Ahli matematik yang hebat dari Pythagoras Antiquity, dilahirkan pada 582 hingga.C di Samos, Greece, mengasaskan Sekolah Pemikiran Pythagorean dan menemui teorem terkenal yang menanggung namanya. Kita turun ke kiri (orang Babilonia sudah dapat mengenalnya lama sebelum ini).

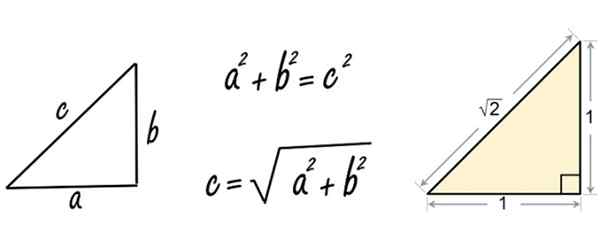Rajah 2. Teorem Pythagoras digunakan untuk segitiga sisi sama dengan 1. Sumber: Pixabay/Wikimedia Commons.

Nah, ketika Pythagoras (atau mungkin pengikutnya) memohon teorem ke segitiga kanan sisi sama dengan 1, mendapati nombor tidak rasional √2.

Ia dapat melayani anda: garisan pengeringan

Dia melakukannya dengan cara ini:

C = √1² + 1² = √1+1 = √2

Dan dia segera menyedari bahawa nombor baru ini tidak datang dari kuota antara dua nombor semula jadi yang lain, yang mana yang diketahui pada masa itu.

Oleh itu dia memanggilnya tidak rasional, Dan penemuan itu menyebabkan kebimbangan dan kekeliruan yang besar di kalangan orang Pythagore.

Sifat nombor yang tidak rasional

-Set semua nombor tidak rasional dilambangkan dengan huruf saya dan kadang -kadang seperti q* atau q^C. Kesatuan antara nombor yang tidak rasional I atau Q* dan nombor rasional Q, menimbulkan set nombor N sebenar.

-Dengan nombor yang tidak rasional, operasi aritmetik yang diketahui dapat dilakukan: jumlah, penolakan, pendaraban, pembahagian, potentiasi dan banyak lagi.

-Pembahagian antara 0 tidak ditakrifkan di antara nombor yang tidak rasional.

-Jumlah dan produk antara nombor tidak rasional tidak semestinya nombor yang tidak rasional. Sebagai contoh:

√2 x √8 = √16 = 4

Dan 4 bukan nombor yang tidak rasional.

-Walau bagaimanapun, jumlah nombor rasional ditambah yang tidak rasional menyebabkan tidak rasional. Cara ini:

1 + √2 = 2.41421356237 ..

-Produk nombor rasional yang berbeza dari 0 dengan nombor tidak rasional juga tidak masuk akal. Mari lihat contoh ini:

2 x √2 = 2.828427125 ..

-Kebalikan dari hasil yang tidak rasional dalam nombor yang tidak rasional yang lain. Mari cuba beberapa:

1 / √2 = 0.707106781 ..

1 / √3 = 0.577350269 ..

Nombor -nombor ini menarik kerana mereka juga nilai -nilai beberapa sebab trigonometri sudut yang diketahui. Kebanyakan sebab trigonometri adalah nombor yang tidak rasional, tetapi ada pengecualian, seperti sen 30º = 0.5 = ½, yang rasional.

-Dalam jumlah itu, sifat komutatif dan bersekutu dipenuhi. Jika A dan B adalah dua nombor yang tidak rasional, ini bermakna:

Boleh melayani anda: Fungsi overjective: definisi, sifat, contoh

A + b = b + a.

Dan jika C adalah nombor yang tidak rasional, maka:

(A + b) + c = a + (b + c).

-Harta pendaraban pengedaran berkenaan dengan jumlah itu adalah satu lagi harta yang diketahui yang juga dipenuhi untuk nombor yang tidak rasional. Dalam kes ini:

ke.(b+c) = a.B + a.c.

-Yang tidak rasional mempunyai sebaliknya: -a. Apabila hasilnya ditambah, ia adalah 0:

A+(-a) = 0

-Antara dua yang berbeza rasional, terdapat sekurang -kurangnya satu nombor yang tidak rasional.

Lokasi nombor yang tidak rasional di garisan sebenar

Garis sebenar adalah garis mendatar di mana nombor sebenar terletak, di mana tidak rasional adalah bahagian penting.

Untuk mencari nombor yang tidak rasional pada garis sebenar, dalam bentuk geometri, kita boleh bernilai teorem pythagoras, peraturan dan kompas.

Sebagai contoh, kita akan mencari √5 pada garis sebenar, yang mana kita melukis segitiga segi empat tepat x = 2 dan y = 1, Seperti yang ditunjukkan oleh gambar:

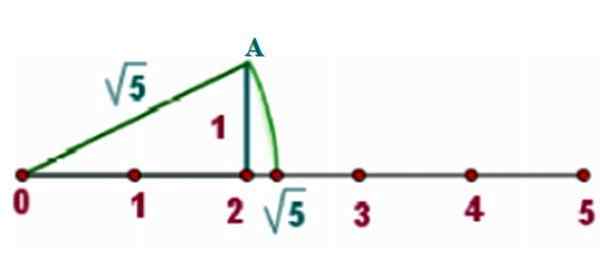Rajah 3. Kaedah untuk mencari nombor yang tidak rasional pada baris sebenar. Sumber: f. Zapata.

Untuk teorem Pythagoras, hipotenus segitiga seperti itu adalah:

C = √2² + 1² = √4+1 = √5

Sekarang pukulan dengan hujung diletakkan di 0, di mana terdapat juga salah satu simpang segitiga yang betul. Hujung pensil kompas mesti berada di puncak.

Arka lilitan ditarik yang memotong garis sebenar. Oleh kerana jarak antara pusat lilitan dan mana -mana titik yang sama adalah jejari, yang bernilai √5, titik persimpangan juga √5 dari pusat.

Graf yang dilihat bahawa √5 adalah antara 2 dan 2.5. Kalkulator menawarkan kami nilai anggaran:

Boleh melayani anda: Koefisien penentuan: formula, pengiraan, tafsiran, contoh

√5 = 2.236068

Oleh itu, membina segitiga dengan sisi yang sesuai, yang lain yang tidak rasional dapat ditempatkan, seperti √7 dan lain -lain.

Klasifikasi nombor yang tidak rasional

Nombor tidak rasional diklasifikasikan kepada dua kumpulan:

-Algebra

-Transenden atau transendental

Nombor algebra

Nombor algebra, yang boleh menjadi tidak rasional atau tidak, adalah penyelesaian persamaan polinomial yang bentuk umumnya:

ke_n xⁿ + ke_N-1x^N-1 + ke_N-2x^N-2 +… . +ke₁x + a_{Sama ada} = 0

Contoh persamaan polinomial adalah persamaan darjah kedua seperti ini:

x³ - 2x = 0

Sangat mudah untuk menunjukkan bahawa nombor tidak rasional √2 adalah salah satu penyelesaian persamaan ini.

Nombor transenden

Sebaliknya, nombor transenden, walaupun tidak rasional, tidak pernah timbul sebagai penyelesaian persamaan polinomial.

Nombor transenden yang paling kerap dijumpai dalam matematik yang digunakan adalah π, kerana hubungan mereka dengan lilitan dan nombor E, atau nombor euler, yang merupakan asas logaritma Neperian.

Senaman

Di dataran hitam kelabu diletakkan di kedudukan yang ditunjukkan dalam angka itu. Diketahui bahawa permukaan dataran hitam adalah 64 cm². Berapa panjang kedua dataran?

Rajah 4. Dua dataran, yang mana panjangnya dapat dijumpai. Sumber: f. Zapata.

Jawapan

Permukaan persegi sisi L ialah:

A = L²

Kerana dataran hitam adalah 64 cm² kawasan, sisinya mestilah 8 cm.

Ukuran ini sama dengan Pepenjuru dataran kelabu. Memohon teorem Pythagoras ke pepenjuru ini, dan mengingati bahawa sisi persegi mengukur sama, kita akan mempunyai:

8² = L_g² + L_g²

Di mana l_g Ia adalah sisi dataran kelabu.

Oleh itu: 2L_g² = 8²

Memohon akar persegi di kedua -dua belah persamaan:

L_g = (8/√2) cm

Rujukan

1. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
2. Figuera, j. 2000. Matematik ke -9. Ijazah. Edisi bersama.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Portal pendidikan. Nombor yang tidak rasional dan sifat mereka. Diperolehi daripada: portaleducative.jaring.
5. Wikipedia. Nombor tidak rasional. Pulih dari: Adakah.Wikipedia.org.