Nombor sempurna bagaimana mengenal pasti dan contohnya

A Nombor sempurna adalah nombor semula jadi seperti itu Jumlah pembahaginya adalah sama dengan nombornya. Jelas sekali ia tidak dapat disertakan di kalangan pembahagi dengan nombor itu sendiri.

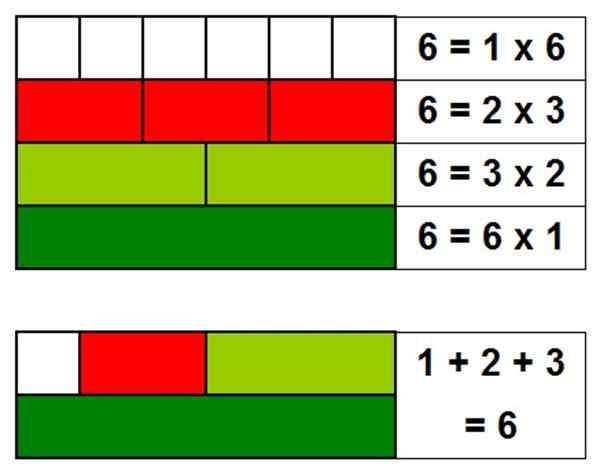
Salah satu contoh paling mudah dari nombor sempurna adalah 6, kerana pembahaginya ialah: 1, 2 dan 3. Jika kita menambah pembahagi, ia diperolehi: 1 + 2 + 3 = 6.

Rajah 1. Nombor 6 adalah sempurna, kerana jumlah pembahaginya, tidak termasuk nombor itu sendiri, memberikan nombor 6. Sumber: Diri Diri

Jumlah pembahagi integer, tidak termasuk nombor itu sendiri, dipanggil aliquot. Oleh itu bilangan yang sempurna adalah sama dengan aliquotnya.

Tetapi jika dalam jumlah pembahagi nombor nombor itu sendiri dimasukkan, maka jumlah yang sempurna akan menjadi satu jumlah semua pembahagi yang dibahagikan dengan 2 adalah sama dengan nombor itu sendiri.

[TOC]

Sejarah

Para ahli matematik zaman dahulu, terutamanya orang Yunani, memberi kepentingan besar kepada bilangan yang sempurna dan kualiti ilahi yang dikaitkan.

Sebagai contoh, Philo de Alejandría, sekitar abad ke -1, mendakwa bahawa 6 dan 28 adalah nombor sempurna yang bertepatan dengan enam hari penciptaan dunia dan dua puluh hari yang diperlukan untuk bulan untuk menghidupkan bumi.

Nombor yang sempurna juga terdapat dalam alam semula jadi, contohnya di tiang utara Saturnus juga muncul nombor 6 yang sempurna, vorteks berbentuk segi enam yang ditemui oleh siasatan Cassini dan yang tertarik kepada saintis. 

Lebah lebah lebah mempunyai sel dalam bentuk heksagon, iaitu dengan 6 sisi.  Ditunjukkan bahawa poligon dengan nombor 6 yang sempurna adalah yang membolehkan memaksimumkan bilangan sel di sarang lebah, dengan lilin minimum untuk penjelasannya.

Rajah 2. Nombor 6 yang sempurna hadir di lebah sarang lebah. Ditunjukkan bahawa dengan bilangan sisi ini jumlah lilin yang akan digunakan untuk membentuk sel adalah minimum. Sumber: Pixabay.

Sifat nombor sempurna

Jumlah semua pembahagi bilangan semula jadi n dilambangkan oleh σ (n). Dalam jumlah yang sempurna memang benar bahawa: σ (n) = 2n.

Formula dan Kriteria Euclid

Euclid menemui formula dan kriteria yang membolehkan anda mencari nombor yang sempurna. Formula ini adalah:

2^(N-1) (2ⁿ -1)

Walau bagaimanapun, bilangan yang dihasilkan oleh formula akan sempurna hanya apabila faktor (2ⁿ -1) Jadilah sepupu.

Boleh melayani anda: komponen segi empat tepat vektor (dengan latihan)

Mari lihat bagaimana nombor sempurna pertama dihasilkan:

Jika n = 2 maka kita mempunyai 2¹ (2² - 1) = 2 x 3 = 6 bahawa kita sudah melihat bahawa ia sempurna.

Apabila n = 3 anda mempunyai 2² (2³ - 1) = 4 x 7 = 28 yang juga sempurna kerana ia disahkan secara terperinci dalam Contoh 1.

Mari lihat apa yang berlaku dengan n = 4. Dengan menggantikan formula Euclid yang kita ada:

2³ (2⁴ - 1) = 8 x 15 = 120

Ia dapat disahkan bahawa nombor ini tidak sempurna, seperti yang ditunjukkan secara terperinci dalam Contoh 3. Ini tidak bertentangan dengan kriteria Euclid, kerana 15 bukan sepupu, keperluan yang diperlukan untuk hasilnya menjadi nombor yang sempurna.

Mari lihat apa yang berlaku ketika n = 5. Memohon formula yang kita ada:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Sebagai 31 adalah nombor perdana, jadi nombor 496 harus sempurna, menurut kriteria Euclid. Dalam Contoh 4 ia ditunjukkan secara terperinci bahawa ia berkesan.

Nombor Perdana yang mempunyai Borang 2^p - 1 Mereka dipanggil sepupu Mersenne, sebagai penghormatan kepada Monk Marin Mersenne, yang mempelajari nombor utama dan nombor yang sempurna pada abad ketujuh belas.

Selanjutnya pada abad kelapan belas Leonhard Euler menunjukkan bahawa semua nombor sempurna yang dihasilkan oleh formula Euclid adalah pasangan.

Sehingga kini, sempurna telah dijumpai yang ganjil.

Nombor sempurna terbesar yang diketahui

Ke tarikh semasa 51 nombor sempurna diketahui, semuanya dihasilkan oleh kriteria formula dan euclid. Nombor ini diperoleh apabila sepupu Mersenne ditemui, iaitu: (2^82589933 - 1).

Nombor sempurna #51 adalah (2^82589933) X (2^82589933 - 1) dan mempunyai 49724095 digitos.

Nombor yang sempurna adalah rakan diri anda

Dalam teori nombor dikatakan bahawa dua nombor adalah kawan apabila jumlah pembahagi satu, tidak termasuk nombor itu sendiri, sama dengan nombor lain dan sebaliknya.

Ia boleh melayani anda: segmen baris dan separuh

Pembaca dapat mengesahkan bahawa jumlah pembahagi 220, tidak termasuk 220 adalah 284. Sebaliknya, jumlah pembahagi 284, tidak termasuk 284, bersamaan dengan 220. Oleh itu pasangan nombor 220 dan 284 adalah kawan.

Dari sudut pandangan ini, jumlah yang sempurna adalah kawan diri anda.

Contoh nombor sempurna

Seterusnya, lapan nombor sempurna pertama disenaraikan:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Latihan

Dalam latihan berikut, diperlukan untuk mengira pembahagi nombor, dan kemudian buat jumlahnya dan sahkan jika nombor itu adalah nombor yang sempurna atau tidak.

Oleh itu sebelum menangani latihan, kami akan mengkaji semula konsep dan menunjukkan bagaimana ia dikira.

Bermula, anda harus ingat bahawa nombor boleh menjadi sepupu (apabila mereka hanya boleh dibahagikan dengan tepat dengan diri mereka sendiri dan 1) atau sebatian (apabila mereka boleh terurai sebagai produk nombor perdana).

Untuk nombor kompaun dan anda mempunyai:

N = aⁿ . b^m. c^p ... r^k 

Di mana A, B, C ... R adalah Nombor Perdana dan N, M, P ... k adalah eksponen yang dimiliki oleh nombor semula jadi, yang boleh bernilai dari 1 dan seterusnya.

Dari segi eksponen ini, terdapat formula untuk mengetahui berapa banyak pembahagi yang ada di Nombor N, walaupun tidak memberitahu kita apa ini. Biarkan C menjadi jumlah ini, maka:

C = (n +1) (m +1) (p +1) ... (k +1)

Penguraian nombor N sebagai produk nombor perdana dan pengetahuan tentang berapa banyak pembahagi, kedua -dua sepupu dan bukan cousin, akan membantu kita menentukan apakah pembahagi ini.

Sebaik sahaja semua orang mempunyai, kecuali yang terakhir yang tidak diperlukan dalam jumlah, ia dapat disahkan sama ada ia adalah nombor yang sempurna atau tidak.

- Latihan 1

Sahkan nombor 28 itu sempurna.

Penyelesaian

Yang pertama adalah untuk menguraikan nombor dalam faktor utama.

28 | 2
14 | 2
07 | 7
01 | 1

Pembahagi adalah: 1, 2, 4, 7, 14 dan 28. Sekiranya kita mengecualikan pada 28 jumlah pembahagi memberi:

Boleh melayani anda: separuh daripada 15

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Oleh itu 28 adalah nombor yang sempurna.

Di samping itu, jumlah semua pembahagi adalah 28 + 28 jadi peraturan σ (28) = 2 x 28.

- Latihan 2

Tentukan sama ada nombor 38 adalah sempurna atau tidak.

Penyelesaian

Nombor itu dipecah menjadi faktor utama:

39 | 3
13 | 13
01 | 1

Pembahagi 39 tanpa memasukkan nombor itu sendiri adalah: 1, 3 dan 13. Jumlah 1 + 3 + 13 = 4 + 13 = 17 tidak sama dengan 39, oleh itu 39 adalah nombor yang tidak sempurna atau tidak sempurna. 

- Latihan 3

Ketahui sama ada nombor 120 adalah sempurna atau tidak sempurna.

Penyelesaian

Nombor itu dipecah menjadi faktor utama:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Dari faktor utama, pembahagi dijumpai:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 dan 120

Jika 120 adalah sempurna apabila menambahkan semua pembahagi harus diperoleh 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Hasil ini jelas berbeza dari 240, jadi disimpulkan bahawa nombor 120 bukan nombor yang sempurna.

- Latihan 4

Sahkan nombor 496, yang diperolehi oleh kriteria Euclid, adalah nombor yang sempurna.

Penyelesaian

Nombor 496 dipecah menjadi faktor utama:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Maka pembahagi mereka adalah:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Sekarang semuanya ditambah, kecuali 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Mengesahkan bahawa ia adalah nombor yang sempurna.

Rujukan

1. Baldor, a. 1986. Aritmetik. Edisi dan Pengagihan Edisi Codex.
2. Semua mengenai nombor Perdana. Nombor rakan. Pulih dari: jururawat.org.
3. Wolfram Mathworld. Peraturan Euler. Pulih dari: Mathworld.Wolfram.com.
4. Wolfram Mathworld. Nombor sempurna. Pulih dari: Mathworld.Wolfram.com.
5. Wikipedia. Nombor sempurna. Diperoleh dari: dalam.Wikipedia.org.
6. Wikipedia. Nombor rakan. Pulih dari: Adakah.Wikipedia.org.