Nombor transenden iaitu, formula, contoh, latihan

The nombor transenden Mereka adalah yang tidak dapat diperoleh sebagai hasil dari persamaan polinomial. Kebalikan dari nombor transenden adalah nombor algebra, yang merupakan penyelesaian persamaan polinomial jenis:

ke_n xⁿ + ke_N-1 x^N-1 +... + a₂ x² + ke₁ x + a₀ = 0

Di mana koefisien ke_n, ke_N-1,... ke₂, ke₁, ke₀ Mereka adalah nombor rasional, yang dipanggil Koefisien polinomial. Sekiranya nombor x adalah penyelesaian persamaan sebelumnya, maka nombor itu tidak transenden.

Rajah 1. Dua jumlah yang sangat penting dalam sains adalah nombor transenden. Sumber: Domainpartures awam.jaring.

Kami akan menganalisis beberapa nombor dan melihat sama ada atau tidak mereka transenden:

a) 3 tidak transenden kerana ia adalah penyelesaian x - 3 = 0.

b) -2 tidak boleh transenden kerana ia adalah penyelesaian x + 2 = 0.

c) ⅓ Ini adalah 3x - 1 = 0 penyelesaian

d) Penyelesaian persamaan x² - 2x + 1 = 0 adalah √2 -1, jadi kata nombor mengikut definisi tidak transenden.

e) Nor adalah √2 kerana ia adalah hasil persamaan x² - 2 = 0. Dengan menaikkan √2 persegi ia menghasilkan 2, yang dikurangkan dari 2 tidak penting kepada sifar. Jadi √2 adalah nombor yang tidak rasional tetapi tidak transenden.

[TOC]

Apakah nombor transenden?

Masalahnya ialah tidak ada peraturan umum untuk mendapatkannya (kemudian kita akan mengatakan bentuk), tetapi beberapa yang paling terkenal adalah bilangannya pi dan juga Nombor NEPER, dilambangkan masing -masing oleh: π dan dan.

Nombor π

Jumlah π Secara semulajadi nampaknya mengamati bahawa kota matematik antara perimeter p bulatan dan diameternya, tanpa mengira sama ada bulatan kecil atau besar, selalu memberikan nombor yang sama, yang dipanggil pi:

π = P/D ≈ 3,14159 ..

Ini bermakna jika diameter lilitan diambil sebagai unit pengukuran, bagi mereka semua, sama ada besar atau kecil, perimeter akan sentiasa bernilai p = 3.14 ... = π, Seperti yang dapat dilihat dalam animasi Rajah 2.

Boleh melayani anda: Teorem Bolzano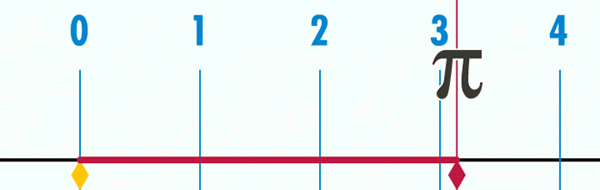Rajah 2. Panjang perimeter bulatan kadang -kadang panjang diameter, iaitu kira -kira 3.1416.

Untuk menentukan lebih banyak perpuluhan, anda perlu mengukur lebih tepat p dan d dan kemudian mengira kuota, yang telah dilakukan dengan cara matematik. Kesimpulannya adalah bahawa perpuluhan kuota tidak mempunyai akhir dan tidak pernah diulang, jadi nombornya π Selain menjadi transenden, ia juga tidak rasional.

Nombor yang tidak rasional adalah nombor yang tidak dapat dinyatakan sebagai pembahagian dua nombor keseluruhan. 

Diketahui bahawa setiap nombor transenden tidak rasional, tetapi tidak benar bahawa semua yang tidak rasional adalah transenden. Contohnya √2 adalah tidak rasional, tetapi tidak transenden.

Rajah 3. Nombor transenden tidak rasional, tetapi pernyataan timbal balik tidak benar.

Nombor e

Nombor transenden adalah asas logaritma Neperian dan pendekatan perpuluhan mereka adalah:

E ≈ 2.718281828459045235360 .. .

Sekiranya anda mahu menulis nombornya dan Tepat sekali, perlu menulis perpuluhan tak terhingga, kerana setiap nombor transenden tidak rasional, seperti yang dikatakan sebelumnya.

Sepuluh digit pertama dan Mereka mudah diingat:

2.7 1828 1828 Dan walaupun nampaknya mengikuti corak berulang, ini tidak dicapai dalam perpuluhan pesanan lebih besar daripada sembilan.

Definisi yang lebih formal mengenai dan adalah yang seterusnya:

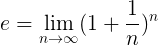
Yang bermaksud bahawa nilai tepat dari dan Operasi yang ditunjukkan dalam formula ini dicapai, apabila nombor semula jadi n Ia cenderung kepada tak terhingga.

Ini menjelaskan mengapa kita hanya dapat memperoleh pendekatan untuk dan, Oleh kerana namun jumlah besar N diletakkan, anda sentiasa dapat mencari n orang tua.

Mari cari beberapa pendekatan anda sendiri:

-Bila n = 100 kemudian (1 + 1/100)¹⁰⁰ = 2,70481 yang hampir tidak bertepatan dengan perpuluhan pertama dengan nilai "benar" e.

-Sekiranya anda dipilih n = 10.000 anda ada (1 + 1/10.000)^10.000 = 2,71815 yang bertepatan dengan nilai "tepat" E dalam tiga perpuluhan pertama.

Boleh melayani anda: sisi homolog

Proses ini harus diikuti untuk dapat memperoleh nilai "benar" e. Saya tidak fikir kita mempunyai masa untuk mencapainya, tetapi mari kita buat satu lagi percubaan:

Mari gunakan n = 100.000:

(1 + 1/100.000)^100.000 = 2.7182682372

Bahawa ia hanya mempunyai empat perpuluhan yang bertepatan dengan nilai yang dianggap tepat.

Yang penting ialah memahami bahawa semakin besar nilai n dipilih untuk mengira dan_n, lebih dekat akan menjadi nilai sebenar. Tetapi nilai sebenar hanya akan diadakan apabila n tidak terhingga.

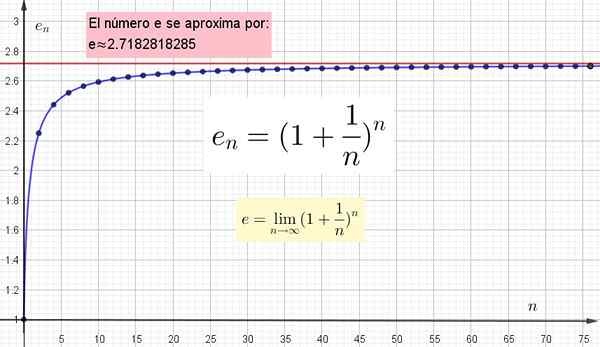Rajah 4. Ia ditunjukkan secara grafik kerana nilai n yang lebih tinggi lebih dekat dengan e, tetapi untuk mencapai nilai yang tepat n mestilah tak terhingga.

Nombor transenden lain

Selain daripada nombor -nombor yang terkenal ini terdapat nombor transenden lain, sebagai contoh:

- 2^√2

Sebarang nombor algebra, yang tidak 0 atau 1, ditinggikan ke eksponen yang tidak rasional akan menjadi nombor transenden.

-Nombor 10 Champernowne: 

C_10 = 0.123456789101112131415161718192021 .. .

-Nombor Champernowne di pangkalan 2:

C_2 = 0.110111001011011 .. .

-Γ atau bilangan gamma berterusan Euler-Mascheroni:

γ ≈ 0.577 215 664 901 532 860 606

Yang diperoleh dengan melakukan pengiraan berikut:

γ ≈ 1 + ½ + ⅓ + ¼ + ... + 1/n - ln (n)

Bila n Jadilah sangat besar. Mempunyai nilai tepat nombor gamma yang diperlukan untuk dikira n tak terhingga. Sesuatu yang serupa dengan apa yang kita lakukan di atas.

Dan terdapat lebih banyak nombor transenden. Ahli matematik yang hebat Georg Cantor, dilahirkan di Rusia dan tinggal antara tahun 1845 dan 1918, menunjukkan bahawa set nombor transenden jauh lebih besar daripada set nombor algebra.

Formula di mana nombor transenden π muncul

Perimeter lilitan

P = π d = 2 π r, di mana p adalah perimeter, d diameter dan r jejari lilitan. Harus diingat bahawa:

Boleh melayani anda: Berapa banyak yang perlu anda tambahkan hingga 3/4 untuk mendapatkan 6/7?

-Diameter lilitan adalah segmen terpanjang yang bergabung dengan dua titik dan yang selalu melalui pusatnya,

-Radius adalah separuh daripada diameter dan segmen yang pergi dari pusat ke tepi.

Kawasan bulatan

A = π r² = ¼ π d²

Permukaan sfera

S = 4 π r^2.

Yeah. Walaupun tidak kelihatan, permukaan sfera adalah sama dengan empat lingkaran jejari yang sama dengan sfera.

Jumlah sfera

V = 4/3 π r³

Latihan

- Latihan 1

Pizzeria "eksotik" menjual tiga pizza diameter: 30 cm kecil, median 37 cm dan besar 45 cm. Seorang kanak -kanak sangat lapar dan menyedari bahawa dua pizza kecil mempunyai kos yang sama seperti yang besar. Apa yang lebih baik baginya, membeli dua pizza kecil atau besar?

Rajah 5.- Kawasan pizza berkadar dengan segi empat jejari, yang tetap berkadar. Sumber: Pixabay.

Penyelesaian

Semakin besar kawasan ini, semakin besar jumlah pizza, oleh sebab itu kawasan pizza besar akan dikira dan dibandingkan dengan dua pizza kecil:

Kawasan pizza besar = ¼ π d² = ¼ ⋅3,1416 ⋅45² = 1590.44 cm²

Kawasan pizza kecil = ¼ π d² = ¼ ⋅3,1416 ⋅30² = 706.86 cm²

Oleh itu dua pizza kecil akan mempunyai kawasan 

2 x 706.86 = 1413.72 cm² .

Jelas: akan ada lebih banyak pizza membeli satu besar daripada dua anak kecil.

- Latihan 2

Pizzeria "eksotik" juga menjual separa radius 30 cm -pizza untuk bentuk segi empat tepat yang sama dengan sisi 30 x 40 cm. Yang akan anda pilih?

Rajah 6.- Permukaan separa -speaker adalah dua kali permukaan bulat asas. Sumber: f. Zapata.

Penyelesaian

Seperti yang dinyatakan di bahagian sebelumnya, permukaan sfera adalah empat kali lebih besar daripada bulatan diameter yang sama, jadi separuh diameter 30 cm akan mempunyai:

30 cm Semi -Man -Pizza: 1413.72 cm² (dua kali bulat diameter yang sama)

Pizza segi empat tepat: (30 cm) x (40 cm) = 1200 cm² .

Semi -man -pizza mempunyai kawasan yang lebih besar.

Rujukan

1. Fernández J. Nombor e. Asal dan Curiosities. Pulih dari: Matematik soya.com
2. Nikmati matematik. Nombor Euler. Pulih dari: nikmatMatimaticas.com.
3. Figuera, j. 2000. Matematik 1st. Dipelbagaikan. Edisi bersama.
4. Garcia, m. Nombor e dalam pengiraan asas. Pulih dari: matematik.Ciens.UCV.Pergi.
5. Wikipedia. Nombor pi. Pulih dari: wikipedia.com
6. Wikipedia. Nombor transenden. Pulih dari: wikipedia.com