Notasi mengembangkan apa, contoh dan latihan

The notasi yang dibangunkan Ia adalah satu di mana angka berangka dinyatakan sebagai jumlah di mana nilai kedudukan setiap digit yang membentuk nombor itu diambil kira.

Contohnya, ketika menulis angka seperti 2345 setiap digitnya mempunyai hierarki posisional. Membaca digit ekstrem kanan ke kiri, hierarki atau nilai semakin meningkat.

Rajah 1. Dengan sembilan graphem, ada kemungkinan untuk mewakili angka.

Dalam Rajah 2345, digit 5 ​​mewakili lima unit, digit 4 mewakili empat puluhan, 3 sepadan dengan kedudukan ketiga dari kiri ke kanan dan oleh itu 3 mewakili tiga ratus, akhirnya 2 mewakili dua ribu. Iaitu, dalam notasi maju atau dilanjutkan, Rajah 2345 ditulis seperti ini:

2345 = 2 ribu + 3 ratus + 4 puluhan + 5 unit

Tetapi ia juga boleh dinyatakan seperti berikut:

2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.

Rajah 2345 juga boleh ditulis sebagai jumlah kuasa 10:

2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0

Di mana circumflejo ^ bermaksud menaikkan eksponen yang ditunjukkan. Contohnya, 10^3 = 10 x 10 x 10 = 1000. Satu lagi cara menulis eksponen adalah melalui pengawasan:

2345 = 2 x 10³ + 3 x 10² + 4 x 10¹ + 5 x 10⁰

[TOC]

Sistem penomboran kedudukan

Sistem Nombor Arab adalah nombor yang digunakan setiap hari di kebanyakan benua dan negara di dunia. Nombor Arab adalah sistem asas 10 kerana sepuluh simbol atau graphemes digunakan untuk menulis sebarang nombor. Sepuluh simbol ini adalah:

0 1 2 3 4 5 6 7 8 9

Dengan hanya satu daripada simbol ini, angka antara sifar hingga sembilan boleh dinyatakan. Untuk menyatakan angka lebih besar daripada sembilan, sistem kedudukan berdasarkan sepuluh. Rajah 10 adalah sedozen dan sifar unit. Rajah 11 adalah sedozen dan satu unit. Rajah 123 (seratus dua puluh tiga) adalah seratus, dua puluhan dan tiga unit. Ditulis dalam bentuk kuasa sepuluh nombor 123 akan menjadi:

Boleh melayani anda: 60 pembahagi

1 × 10^2 + 2 × 10^1 + 3 × 10^0

Di mana:

10^2 = 10 x 10 = 100

10^1 = 10

10^0 = 1.

Dengan contoh ini jelas bahawa kedudukan digit pada akhirnya adalah kedudukan 0 dan mewakili bilangan unit, yang digit kedua dari kanan ke kiri adalah kedudukan 1 dan mewakili bilangan puluhan, digit ketiga (tepat ke kiri) mempunyai kedudukan 2 dan mewakili beratus -ratus.

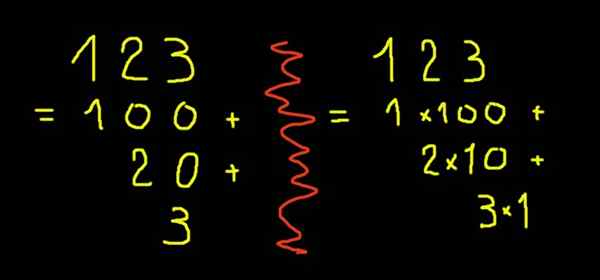Rajah 2. Notasi yang dikembangkan pada Rajah 123.

Nombor pecahan atau perpuluhan

Dengan sistem kedudukan perpuluhan juga mungkin.

Untuk mewakili pecahan ½ dalam sistem perpuluhan Arab, iaitu separuh unit ditulis:

½ = 0.5

Untuk mencapai ungkapan ini dalam sistem kami berdasarkan 10, operasi berikut telah dibuat:

1- Multiply Numentator and Denominator untuk 5 untuk mempunyai pecahan bersamaan 5/10 = 1/2. 

2- Bahagikan dengan 10 bersamaan dengan mendarab dengan kuasa berdasarkan sepuluh dengan eksponen kurang satu (10^-1), iaitu 5/10 = 5 × 10^-1.

3- Eksponen negatif menunjukkan berapa kali digit yang ditunjukkan dari kedudukan unit dijalankan atau diposisikan, dalam kes kita akan menjadi 0.5.

4- ½ = 0.5 Dalam notasi lanjutan ia ditulis seperti ini:

0.5 = 0x10^0 + 5 × 10^-1

Di mana 10^-1 = 0.1 adalah kesepuluh (pecahan sepadan dengan unit yang dibahagikan kepada 10 bahagian yang sama).

Dengan cara ini, nombor 0.5 sepadan dengan lima kesepuluh, tetapi nombor 0.05 sepadan dengan 5 ratus dan 0.005 hingga 5 ribu.

Boleh melayani anda: mengapa algebra penting dalam situasi kehidupan seharian tertentu?

Contoh notasi yang dibangunkan 

Contoh 1

Memandangkan angka 40201 dalam notasi standard, tukarnya ke notasi yang dibangunkan.

Penyelesaian: 

4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201

Contoh 2

Tulis pecahan ¾ dalam notasi lanjutan.

Penyelesaian: 

Dalam kes ini terdapat tiga perempat unit. 

3/4 = 15/20 = 75/100 = 0.75 = 7/10 + 5/100 = 

7 × 10^-1 + 5 × 10^-2.

Kata dengan kata -kata akan seperti ini:

Pecahan ¾ sepadan dengan tujuh sepuluh ditambah lima ratus.

Latihan notasi yang dibangunkan

Latihan 1

Katakan dengan kata -kata ungkapan yang dikembangkan dari angka 40201 Contoh 1.

Penyelesaian:

Notasi yang dibangunkan adalah seperti ini:

40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 

Bahawa dalam bahasa perkataan dikatakan:

Empat puluhan ribu, ditambah ribu ribu, ditambah dua ratus, lebih banyak sifar, ditambah satu unit.

Latihan 2

Menyatakan dengan kata -kata angka sebelumnya dan memecahkan frasa yang sepadan.

Penyelesaian:

Angka 40201 dalam kata -kata dinyatakan seperti berikut:

Empat puluh ribu dua ratus

Frasa sebelumnya boleh berkembang sebagai:

40 × 1000 + 2 × 100 + 1

Boleh dikatakan bahawa cara untuk menyebut angka -angka adalah cara separuh maju untuk menyatakannya.

Latihan 3

Tulis nombor 7/3 yang dibangunkan.

Penyelesaian:

Ia adalah angka yang dinyatakan sebagai pecahan yang tidak wajar, kerana sebagai pengangka lebih besar daripada penyebut, angka itu lebih besar daripada unit.

Fraksi yang tidak betul ini boleh dipecahkan sebagai jumlah pecahan 6/3 + 1/3. Yang pertama dari pecahan menghasilkan keseluruhan nombor 2, manakala 1/3 = 0.333333, di mana digit 3 diulangi selama -lamanya. Supaya ungkapan perpuluhan yang dibangunkan dari angka 7/3 akan selalu menjadi ungkapan anggaran:

Boleh melayani anda: Quadrilateral: Unsur, sifat, klasifikasi, contoh

7/3 = 2 + 1/3 ≃ 2 + 0.333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.

Latihan 6

Tulis dalam notasi standard dan kemudian mengembangkan nombor: Dua puluh tiga bilion dua ratus lima puluh juta lima ratus dua puluh dua ribu tiga ratus dua puluh lima dengan tiga dua puluh tiga ribu.

Penyelesaian:

Harus diingat bahawa a Millardo adalah bersamaan dengan satu bilion. Perkataan itu Millardo Ia diterima oleh Akademi Sepanyol Diraja pada tahun 1995 atas permintaan Presiden Venezuela Rafael Caldera, ahli Akademi Bahasa Venezuela. Dalam hal ini, angka notasi standard ditulis seperti berikut:

23.2501526.325,023

23 bilion + 250 juta + 526 ribu + 325 unit + 23 ribu. 

23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3

Akhirnya angka dalam notasi maju ditulis:

2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.

Rujukan

1. Akademi Khan. Jadual nilai kedudukan. Pulih dari: Adakah.Khanacademy.org
2. Akademi Khan. Tulis nombor maju (video). Pulih dari: Adakah.Khanacademy.org
3. IFRAH, GEOGES (1998): Sejarah Universal Angka. Espasa Calpe s.Ke.
4. Wikipedia. Notasi kedudukan. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Millardo. Pulih dari: Adakah.Wikipedia.com