Formula gelombang pegun, ciri, jenis, contoh

The Gelombang berdiri Mereka adalah gelombang yang tersebar di separuh terhad, pergi dan datang di sebahagian ruang, tidak seperti gelombang perjalanan, yang ketika menyebarkan bergerak dari sumber yang berasal dari mereka dan tidak kembali kepadanya.

Mereka adalah asas bunyi yang dihasilkan dalam alat muzik, kerana mereka muncul dengan mudah pada rentetan tetap, sama ada di salah satu hujungnya atau kedua -duanya. Mereka juga dicipta dalam membran tegang seperti gendang atau tiub dan struktur di dalamnya seperti jambatan dan bangunan.

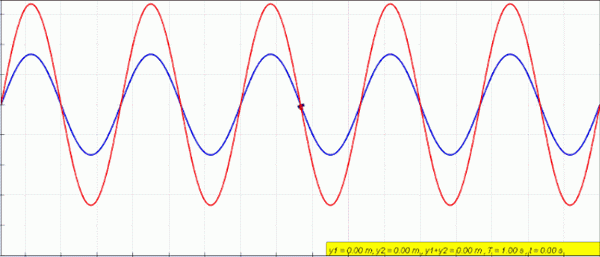Animasi gelombang pegun (merah) yang dicipta oleh superposisi gelombang kiri (biru) dan kanan (hijau). Sumber: Lookangmany terima kasih kepada pengarang Simulasi Asal = Wolfgang Christian dan Francisco Schembre Pengarang Simulasi Easy Java = Francisco Schembre/CC By-SA (https: // creativeCommons.Org/lesen/by-sa/4.0)

Apabila anda mempunyai tali tetap di kedua -dua hujung, seperti gitar, sebagai contoh, gelombang dicipta dengan amplitud dan kekerapan yang sama, yang bergerak dalam deria bertentangan dan menggabungkan menghasilkan fenomena yang dipanggil gangguan.

Sekiranya gelombang berada dalam fasa, rabung dan lembah diselaraskan dan menghasilkan gelombang dengan amplitud berganda. Sekiranya terdapat perbincangan mengenai gangguan yang membina.

Tetapi jika gelombang yang mengganggu fasa, rabung seseorang memenuhi lembah orang lain dan amplitud yang hasilnya adalah sifar. Ia adalah gangguan yang merosakkan.

[TOC]

Formula dan persamaan

Unsur utama gelombang untuk mewakilinya dalam ruang dan masa adalah amplitud A, panjang gelombangnya λ dan kekerapan sudutnya Ω.

Unsur gelombang. Sumber: Wikimedia Commons.

Dalam perwakilan matematik, lebih disukai menggunakan k, daripada Nombor gelombang o bilangan kali gelombang per unit berlaku. Itulah sebabnya ia ditakrifkan melalui panjang gelombang λ yang jarak antara dua lembah atau dua rabung:

K = 2π/ λ

Sementara kekerapan sudut Ia berkaitan dengan tempoh atau tempoh ayunan lengkap, seperti:

Ω = 2π/ t

Dan juga kekerapan f diberikan oleh:

F = Ω / 2π

Oleh itu:

F = 1/t

Di samping itu ombak bergerak dengan kelajuan v Menurut:

V = λ.F

Ekspresi matematik gelombang pegun

Secara matematik kita dapat mengekspresikan gelombang melalui fungsi sinus atau fungsi kosinus. Katakan terdapat gelombang amplitud yang sama A, panjang gelombang λ dan kekerapan Ω, menyebar di sepanjang tali dan dalam deria yang bertentangan:

dan₁ = Dosa (kx - ωt)

dan₂ = Dosa (kx + ωt)

Semasa menambahkannya, kami dapati gelombang yang dihasilkan dan_R:

dan_R = y₁ + dan₂ = Sen (kx - ωt) + dosa (kx + ωt)

Terdapat identiti trigonometri untuk mencari jumlah:

Boleh melayani anda: apa kekasaran relatif dan mutlak?

sin α + sin β = 2 sin (α + β)/2 . COS (α - β)/2

Melalui identiti ini, gelombang yang dihasilkan dan_R ditinggalkan:

dan_R = [2a sen kx] . cos ωt

Lokasi nod dan perut

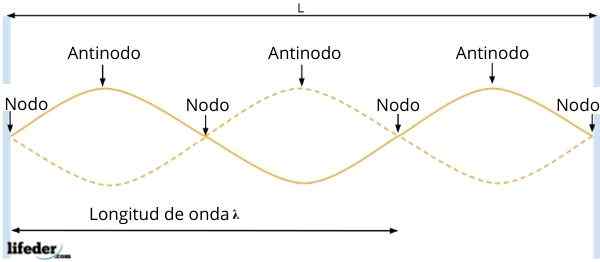Antinodos atau perut dan nod

Gelombang yang dihasilkan mempunyai amplitud untuk_R = 2ase kx, yang bergantung pada kedudukan zarah. Kemudian, pada titik yang mana sen kx = 0, amplitud gelombang dibatalkan, iaitu, tidak ada getaran.

Titik ini adalah:

Kx = π, 2π, 3π ..

Sebagai k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

Di titik sedemikian gangguan merosakkan berlaku dan mereka dipanggil nod. Mereka dipisahkan dengan jarak yang sama dengan λ/2, seperti yang disimpulkan dari hasil sebelumnya.

Dan antara dua nod berturut -turut adalah antinodos atau perut, di mana amplitud gelombang adalah maksimum, kerana gangguan konstruktif berlaku. Mereka berlaku ketika:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Sekali lagi k = 2 π/ λ dan kemudian:

x = λ /4, 3λ /4, 5λ /4, ..

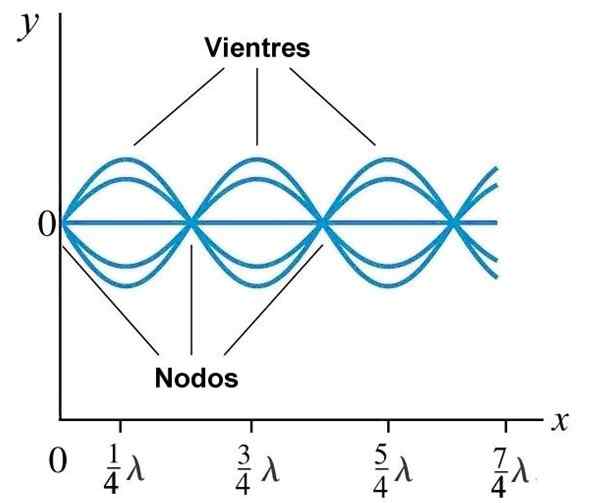Perut atau antinod dan nod dalam gelombang pegun yang dihasilkan pada tali dengan hujung tetap pada x = 0. Sumber: Wikimedia Commons.

Mod biasa pada tali

Keadaan sempadan di tali menentukan bagaimana panjang gelombang dan frekuensi. Sekiranya tali panjang L ditetapkan oleh dua hujungnya, ia tidak dapat bergetar dengan kekerapan apa pun, kerana titik di mana tali tetap sudah nod.

Di samping itu, pemisahan antara nod bersebelahan adalah λ/2, dan di antara nod dan perut ia adalah λ/4, dengan cara ini hanya untuk panjang gelombang tertentu dihasilkan gelombang pegun: yang di mana integer n λ/2 di dalamnya diselaraskan dari diselaraskan dari :

(λ/2) = l, dengan n = 1, 2, 3, 4 .. .

Oleh itu:

λ = 2L/n

Harmonik

Nilai yang berbeza yang diambil λ dipanggil harmonik. Oleh itu kita ada:

-Harmonik Pertama: λ = 2L

-Harmonik Kedua: λ = l

-Harmonik Ketiga: λ = 2 l/3

-Bilik Harmonik: λ = l/2

Dan sebagainya.

Kelajuan dan kekerapan

Walaupun gelombang pegun nampaknya tidak bergerak, persamaan masih sah:

V = λ. F

Oleh itu:

v = (2L/n) . F

F = NV/2L

Sekarang, ia dapat ditunjukkan bahawa kelajuan yang bergerak gelombang dalam tali bergantung kepada voltan T yang sama dan ketumpatan linear jisim μ (jisim per unit panjang) sebagai:

Oleh itu:

Boleh melayani anda: Beban mati: Ciri, pengiraan, contoh

Ciri -ciri gelombang pegun

-Apabila ombak bergerak, gelombang yang dihasilkan tidak tersebar seperti komponennya, yang pergi dari satu tempat ke tempat lain. Terdapat titik di mana y = 0 kerana tidak ada getaran: nod, dengan kata lain, amplitud untuk_R Ia adalah sifar.

-Ekspresi matematik gelombang pegun terdiri daripada produk bahagian ruang (yang bergantung kepada koordinat x atau koordinat ruang) dan bahagian temporal.

-Di antara nod, gelombang hitam yang dihasilkan berayun di satu tempat, sementara gelombang yang pergi dari satu tempat ke tempat lain sudah lapuk di sana.

-Hanya dalam nod, tenaga tidak diangkut, kerana ini berkadar dengan kuadrat amplitud, tetapi terperangkap di antara nod.

-Jarak antara nod bersebelahan adalah separuh panjang gelombang.

-Titik di mana tali tetap juga dianggap nod.

Lelaki

Gelombang pegun dalam dimensi

Gelombang dalam tali tetap adalah contoh gelombang pegun dalam dimensi, yang keterangan matematik yang kami tawarkan di bahagian sebelumnya.

Gelombang pegun dalam dua dan tiga dimensi

Gelombang pegun juga boleh dibentangkan dalam dua dan tiga dimensi, menjadi keterangan matematik yang lebih kompleks.

Contoh Ondas Racing

Rentetan tetap

-Rentetan yang ditetapkan oleh ekstrem yang berayun dengan tangan atau dengan satu omboh oleh yang lain menghasilkan gelombang pegun sepanjang panjangnya.

Alat muzik

Gelombang pegun dicipta dalam alat muzik seperti Violoncello. Sumber: Pixabay.

-Semasa bermain instrumen rentetan seperti gitar, kecapi, biola dan piano.

Gelombang Stlover juga dibuat dalam tiub udara, seperti tiub organ.

Bangunan dan jambatan

Gelombang pegun timbul dalam struktur seperti jambatan dan bangunan. Kes yang luar biasa ialah Jambatan Penggantungan Tacoma Narrows berhampiran City of Seattle, Amerika Syarikat. Tidak lama selepas dirasmikan pada tahun 1940, jambatan ini runtuh kerana gelombang pegun yang dibuat di dalam angin.

Kekerapan angin dipadankan dengan kekerapan semula jadi jambatan, mewujudkan gelombang pegun dalam hal ini, yang meningkatkan amplitud mereka sehingga jambatan runtuh. Fenomena ini dikenali sebagai resonans.

Ia dapat melayani anda: renungan cahaya

Seiches

Di pelabuhan terdapat fenomena yang sangat ingin tahu Seiche, di mana gelombang laut menghasilkan ayunan besar. Ini kerana air di pelabuhan agak tertutup, walaupun perairan lautan menembusi setiap sering melalui pintu masuk pelabuhan.

Port Waters bergerak dengan kekerapan mereka sendiri, dan juga lautan. Jika kedua -dua air sepadan dengan frekuensi mereka, terdapat gelombang pegun yang besar kerana resonans, seperti yang berlaku dengan Jambatan Tacoma.

The Seiches Mereka juga boleh berlaku di tasik, takungan, kolam renang dan badan air lain yang terhad oleh permukaan.

Tangki ikan

Gelombang pegun boleh dibuat dalam ikan ikan yang diangkut oleh seseorang, jika kekerapan yang mana orang itu sama dengan kekerapan ayunan air.

Latihan diselesaikan

Tali gitar mempunyai l = 0.Ketumpatan adunan 9 m dan linear μ = 0.005 kg/m. Ia tertakluk kepada 72 n voltan dan mod getarannya adalah yang menunjukkan angka, dengan amplitud 2a = 0.5 cm.

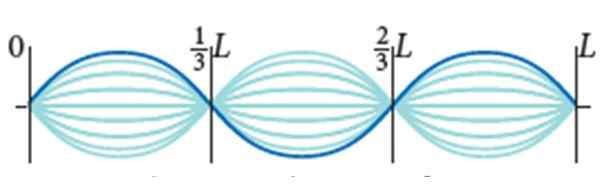Gelombang pegun pada tali gitar. Sumber: Bauer, W. Fizikal.

Cari:

a) kelajuan penyebaran

b) kekerapan gelombang

c) Persamaan gelombang pegun yang sepadan.

Penyelesaian kepada

Melalui:

Diperoleh;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Penyelesaian b

Jarak antara dua nod bersebelahan adalah λ/2, oleh itu:

(2/3) L - (1/3) L = λ/2

(1/3) L = λ/2

λ = 2L/3 = 2 x 0.90 m / 3 = 0.60 m.

Seperti v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Penyelesaian c

Persamaannya adalah:

dan_R = [2a sen kx] . cos ωt

Kita perlu mengganti nilai:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = Ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

Amplitud 2A sudah diberikan oleh pernyataan:

2a = 0.5 cm = 5 x 10 ^-3 m.

Oleh itu:

dan_R = 5 x 10 ^-3 m . dosa [(10π/3) x] . cos (400πt) =

= 0.5 cm . dosa [(10π/3) x] . cos (400πt)

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 7. Gelombang dan Fizik Kuantum. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.
5. Tipler, ms. (2006) Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 1. Editorial kembali.
6. Wikipedia. Seiche. Pulih dari: Adakah.Wikipedia.org.