Perimeter bulatan bagaimana untuk mengeluarkannya dan formula, latihan diselesaikan

Dia perimeter bulatan Ia adalah set mata yang membentuk kontur bulatan dan juga dikenali sebagai panjang dari lilitan. Ia bergantung pada jejari, kerana lilitan yang lebih besar jelas akan mempunyai kontur yang lebih besar.

Menjadi P Perimeter bulatan dan R jejari yang sama, maka kita boleh mengira P Dengan persamaan berikut:

P = 2π.R

Perimeter bulatan (dalam kes ini pizza) bergantung pada radionya. Sumber: Pixabay.

Di mana π adalah nombor sebenar (berbunyi "pi") yang bernilai kira -kira 3.1416 ... Titik yang menggembirakan disebabkan oleh fakta bahawa π mempunyai perpuluhan tak terhingga. Oleh itu, apabila membuat pengiraan, perlu untuk mengelilingi nilainya.

Walau bagaimanapun, bagi kebanyakan aplikasi, sudah cukup untuk mengambil jumlah yang ditunjukkan di sini, atau menggunakan semua perpuluhan yang kalkulator yang berfungsi.

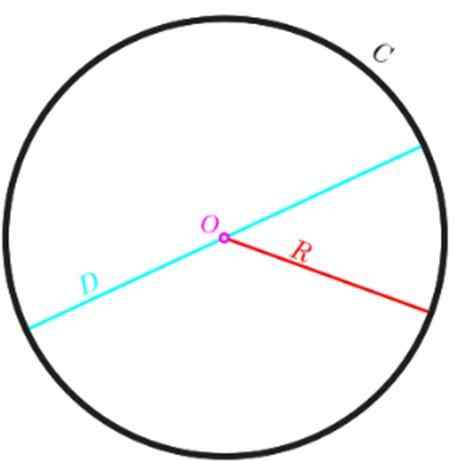
Jika bukannya mempunyai jejari, lebih suka menggunakan diameter d, yang kita tahu adalah dua kali jejari, perimeter dinyatakan seperti berikut:

P = π.2r = π.D

Oleh kerana perimeter adalah panjang, ia mesti selalu dinyatakan dalam unit seperti meter, sentimeter, kaki, inci dan banyak lagi, bergantung kepada sistem yang lebih disukai.

[TOC]

Lingkaran dan bulatan

Mereka sering digunakan secara bergantian, iaitu, sebagai sinonim. Tetapi ia berlaku bahawa terdapat perbezaan di antara mereka.

Perkataan "perimeter" berasal dari bahasa Yunani "Tempoh" yang bermaksud kontur dan "kereta bawah tanah" atau mengukur. Lilitan adalah kontur atau perimeter bulatan. Secara rasmi ia ditakrifkan:

Lilitan adalah set mata dengan jarak yang sama ke titik yang dipanggil pusat, jarak ini menjadi jejari lilitan.

Bagi bahagiannya, bulatan ditakrifkan sebagai berikut:

Bulatan adalah set mata yang jaraknya ke titik yang dipanggil pusat kurang dari atau sama dengan jarak tetap yang disebut radio.

Pembaca dapat memberi amaran kepada perbezaan yang halus antara kedua -dua konsep. Lilitan hanya merujuk kepada set titik tepi, sementara bulatan adalah set titik dari tepi ke dalam, di mana lilitan adalah sempadan.

Boleh melayani anda: Latihan pelepasan formula

Latihan dEmostrasi pengiraan perimeter bulatan

Melalui latihan berikut, konsep yang diterangkan akan dipraktikkan, serta beberapa orang lain yang akan dijelaskan ketika ia muncul. Kami akan bermula dari yang paling mudah dan tahap kesukaran akan meningkat secara progresif.

- Latihan 1

Cari perimeter dan kawasan bulatan radio 5 cm.

Penyelesaian

Persamaan yang diberikan pada mulanya digunakan secara langsung:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Untuk mengira kawasan tersebut Ke Formula berikut digunakan:

Ke = π.R² = π. (5cm)²= 25π cm²= 78.534 cm²

- Latihan 2

a) Cari perimeter dan kawasan kawasan kosong dari angka berikut. Pusat bulatan yang berlorek berada di titik merah, sementara pusat lilitan putih adalah titik hijau.

b) Ulangi bahagian sebelumnya untuk kawasan yang berlorek.

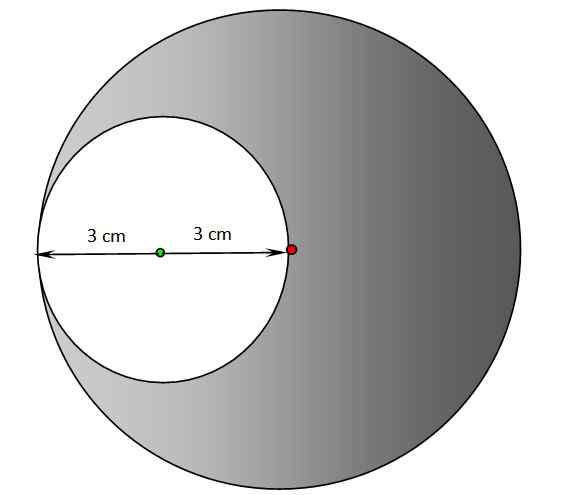Lingkaran untuk Latihan 2. Sumber: f. Zapata.

Penyelesaian

a) Radius lilitan putih adalah 3 cm, oleh itu kita menggunakan persamaan yang sama seperti dalam Latihan 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

Ke = π.R² = π. (3cm)²= 9π cm²= 28.27 cm²

b) Untuk bulatan yang berlorek, jejari adalah 6 cm, perimeternya adalah dua kali ganda yang dikira dalam bahagian a):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

Dan akhirnya kawasan kawasan berlorek dikira seperti berikut:

- Pertama adalah kawasan bulatan yang berlorek seolah -olah ia selesai, yang akan kita panggil ', seperti ini:

Ke ' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Kemudian ke kawasan Ke ' Kawasan bulatan putih dikurangkan, sebelum ini dikira dalam Bahagian A), dengan cara ini kawasan yang diminta diperoleh, yang akan dilambangkan hanya sebagai:

A = A ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Latihan 3

Cari kawasan dan perimeter kawasan yang berlorek dalam angka berikut:

Boleh melayani anda: Sudut Tambahan: Apa, Pengiraan, Contoh, Latihan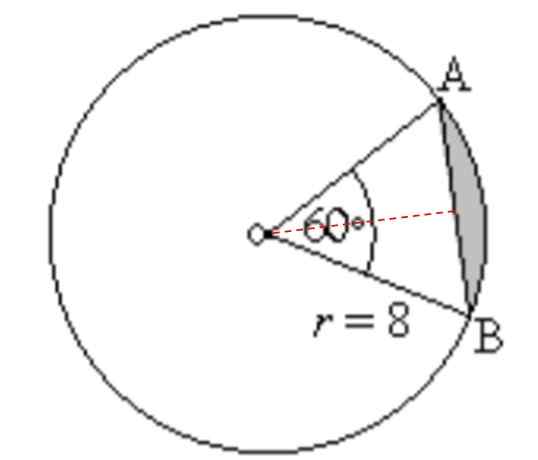Rajah untuk Latihan 3. Sumber: f. Zapata.

Penyelesaian

Pengiraan kawasan kawasan yang berlorek

Kami mula -mula mengira kawasan Sektor Pekeliling atau baji, antara segmen lurus OA dan OB dan segmen AB bulat, seperti yang ditunjukkan dalam angka berikut:

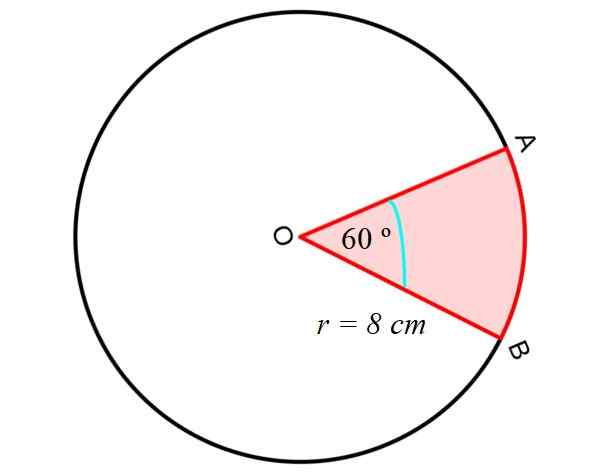
Untuk ini, persamaan berikut digunakan, yang memberi kita kawasan sektor bulat, mengetahui radius r dan sudut pusat antara segmen OA dan OB, iaitu dua radio lilitan:

Ke _{Sektor Pekeliling} = Π.R². (αº/360º)

Di mana αº adalah sudut pusat - ia adalah pusat kerana puncaknya adalah pusat lilitan - antara dua radio.

Langkah 1: Pengiraan Kawasan Sektor Pekeliling

Dengan cara ini, kawasan sektor yang ditunjukkan dalam angka adalah:

Ke _{Sektor Pekeliling} = Π.R². (αº/360º) = π. (8 cm)². (60º/360º) = (64/6) π cm²= 33.51 cm²

Langkah 2: Pengiraan kawasan segitiga

Kemudian kami akan mengira kawasan segitiga putih angka 3. Segitiga ini sama dan kawasannya adalah:

Ke _Segitiga = (1/2) ketinggian x asas

Ketinggiannya adalah garis merah bertitik yang dilihat dalam Rajah 4. Untuk mencarinya, anda boleh menggunakan teorem Pythagoras, sebagai contoh. Tetapi ia bukan satu -satunya cara.

Pembaca pemerhati akan menyedari bahawa segitiga sama rata dibahagikan kepada dua segi empat tepat yang sama, yang asasnya adalah 4 cm:

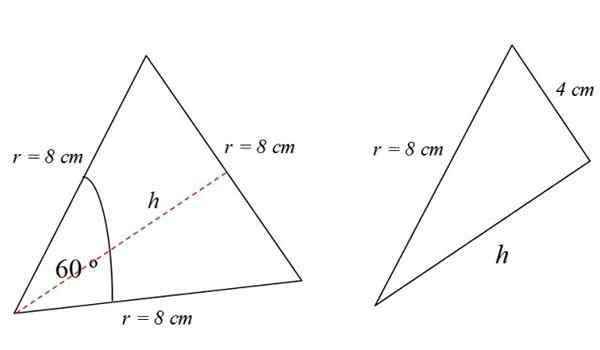
Dalam segitiga yang betul, teorem Pythagoras dipenuhi, oleh itu:

Oleh kerana anda mempunyai ketinggian segitiga, kedua -dua segi empat tepat dan sama, kawasannya dikira:

Ke _Segitiga = (1/2) asas x ketinggian = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Langkah 3: Pengiraan kawasan yang berlorek

Sudah cukup untuk menolak kawasan utama (sektor bulat) kawasan kecil (segitiga sama rata): a _{rantau yang berlorek} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Pengiraan perimeter kawasan yang berlorek

Perimeter yang dicari adalah jumlah sisi rectilinear 8 cm dan arka lilitan ab.  Walau bagaimanapun, lilitan lengkap subtend 360 º, oleh itu arka yang subthes 60 º adalah bahagian keenam panjang penuh, yang kita tahu adalah 2.π.Pada:

Boleh melayani anda: Fungsi Berkembang: Cara Mengenalpasti, Contoh, Latihan

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Menggantikan, perimeter kawasan yang berlorek adalah:

P = 8 cm + 8.38 cm = 16.38 cm.

Aplikasi

Perimeter, seperti kawasan, adalah konsep yang sangat penting dalam geometri dan dengan banyak aplikasi dalam kehidupan seharian.

Artis, pereka, arkitek, jurutera dan banyak orang lain memanfaatkan perimeter semasa membangunkan kerja mereka, terutamanya bulatan, kerana bentuk bulat di mana -mana: dari pengiklanan, melalui makanan ke jentera.

Lingkaran dan bulatan adalah antara geometri yang paling banyak digunakan. Sumber: Pixabay.

Untuk mengetahui secara langsung panjang bulatan, sudah cukup untuk membungkusnya dengan benang atau rentetan, kemudian lanjutkan benang ini dan ukur dengan pita pita. Alternatif lain adalah untuk mengukur jejari atau diameter bulatan dan menggunakan beberapa formula yang diterangkan di atas.

Dalam kerja harian, konsep perimeter digunakan ketika:

-Acuan yang sesuai dipilih untuk saiz pizza atau kek tertentu.

-Jalan Bandar akan direka, dengan mengira saiz redoma di mana kereta boleh berubah menjadi makna.

-Kita tahu bahawa Bumi berkisar di sekitar matahari di orbit kira -kira bulat -dalam realiti orbit planet adalah elips, menurut undang -undang Kepler -tetapi lilitan adalah pendekatan yang sangat baik untuk kebanyakan planet.

-Saiz cincin atau cincin yang sesuai yang akan dibeli di kedai dalam talian dipilih.

-Kami memilih kunci untuk saiz yang betul untuk melonggarkan kacang.

Dan banyak lagi.

https: // youuat.Be/cr8xjryl5tk

Rujukan

1. Tutorial Matematik Percuma. Kawasan dan perimeter bulatan - kalkulator geometri. Pulih dari: analisis.com.
2. Rujukan terbuka matematik. Lilitan, perimeter bulatan. Pulih dari: Mathpenref.com.
3. Institut Monterey. Perimeter dan kawasan. Pulih dari: Montereyinstitute.org.
4. Saintifik. Cara mencari perimeter bulatan. Pulih dari: saintifik.com.
5. Wikipedia. Lilitan. Diperoleh dari: dalam.Wikipedia.org.