Archimedes Prinsip Formula, Demonstrasi, Aplikasi

Dia Prinsip Archimedes Dia mengatakan bahawa badan yang tenggelam sepenuhnya atau sebahagiannya menerima daya menegak yang dipanggil tolak, yang bersamaan dengan berat jumlah cecair yang dipindahkan oleh badan. 

Sesetengah objek terapung di dalam air, yang lain tenggelam dan sebahagiannya merenung diri mereka sendiri. Untuk menenggelamkan bola pantai, perlu membuat usaha, kerana kekuatan itu segera dirasakan yang cuba mengembalikannya ke permukaan. Sebaliknya sfera logam cepat tenggelam. 

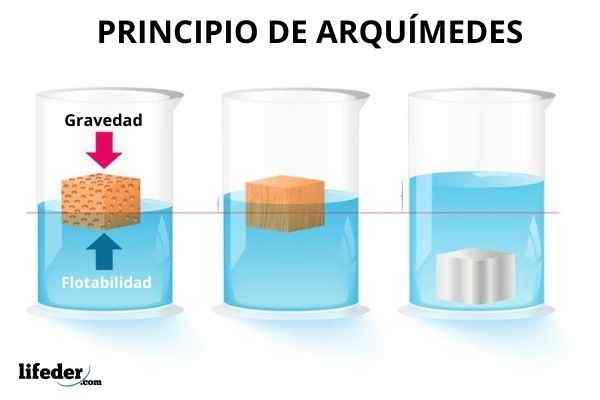
Sebaliknya, objek tenggelam kelihatan lebih ringan, oleh itu terdapat daya yang dikenakan oleh cecair yang menentang berat badan. Tetapi anda tidak boleh mengimbangi sama sekali kepada graviti. Dan, walaupun lebih jelas dengan air, gas juga dapat menghasilkan daya ini pada objek yang direndam di dalamnya.

[TOC]

Sejarah

Archimedes of Syracuse (287-212 a. C.) Ia adalah orang yang mesti menemui prinsip ini, menjadi salah satu saintis terbesar dalam sejarah. Mereka mengatakan bahawa Raja Hierón II dari Syracuse menghantar tukang emas untuk mengeluarkan mahkota baru, yang mana dia menyerahkannya dengan jumlah emas tertentu.

Archimedes

Ketika raja menerima mahkota baru, dia mempunyai berat badan yang tepat, tetapi dia mengesyaki bahawa tukang emas itu menipu dia dengan menambahkan perak dan bukannya emas. Bagaimana saya boleh memeriksanya tanpa memusnahkan mahkota?

Hierón dipanggil Archimedes, yang terkenal dengan ulama yang terkenal, untuk membantunya menyelesaikan masalah. Legenda itu menegaskan bahawa Archimedes telah direndam di dalam tab mandi ketika dia mendapati jawapannya dan, itu adalah emosinya, bahawa dia berlari telanjang melalui jalan -jalan di Syracuse untuk mencari raja yang menjerit "Eureka", yang bermaksud "saya dapati ia".

https: // giphy.com/gifs/stito3echtlnbvliz3

Apa yang dicari oleh Archimedes? Nah, ketika mengambil bilik mandi paras air di dalam tab mandi, ketika dia masuk, yang bermaksud bahawa badan tenggelam menggantikan jumlah cecair tertentu.

Dan jika saya tenggelam mahkota di dalam air, ia juga harus memindahkan jumlah air tertentu jika mahkota itu diperbuat daripada emas dan yang berbeza jika ia diperbuat daripada aloi dengan perak.

Formula Prinsip Archimedes

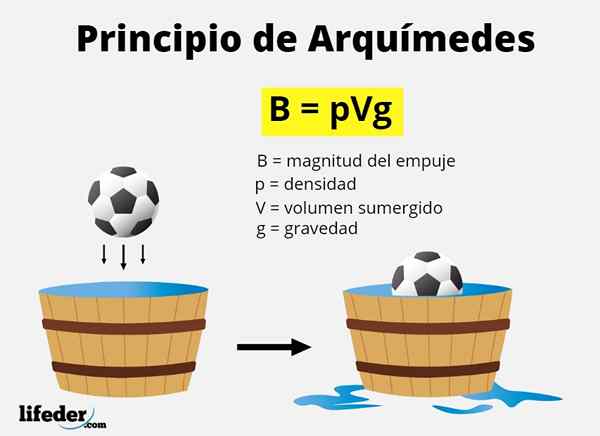
Daya promosi yang disebut dalam prinsip Archimedes dikenali sebagai tolak Hydrostatic Sama ada daya pengapungan Dan, seperti yang telah kita katakan, ia bersamaan dengan berat jumlah bendalir yang dipindahkan oleh badan ketika tenggelam.

Jumlah yang dipindahkan bersamaan dengan jumlah objek yang tenggelam, sama ada sepenuhnya atau sebahagiannya. Oleh kerana berat apa -apa adalah mg, Dan jisim bendalir adalah Ketumpatan x volum, Menafikan bagaimana B ke magnitud tujahan, secara matematik ia harus:

B = m_fasih x g = ketumpatan bendalir x tenggelam volum x graviti

B = ρ_fasih x v_tenggelam x g

Di mana huruf Yunani ρ ("rho") menandakan ketumpatan.

Berat badan yang jelas

Berat objek dikira oleh ungkapan yang terkenal mg, Walau bagaimanapun, perkara -perkara yang lebih ringan apabila mereka tenggelam di dalam air. 

Dia berat badan yang jelas objek adalah apa yang telah direndam di dalam air atau cecair lain dan mengetahui, anda boleh mendapatkan jumlah objek yang tidak teratur seperti mahkota Raja Hierón, seperti yang akan dilihat di bawah.

Boleh melayani anda: 13 contoh undang -undang pertama Newton dalam kehidupan sebenar

Untuk melakukan ini, ia sepenuhnya tenggelam di dalam air dan tertakluk kepada tali yang dilampirkan pada a Dynamometer -instrumen yang disediakan dengan musim bunga yang berfungsi untuk mengukur daya-. Semakin besar berat objek, semakin besar pemanjangan musim bunga, yang diukur pada skala yang disediakan dalam peranti.

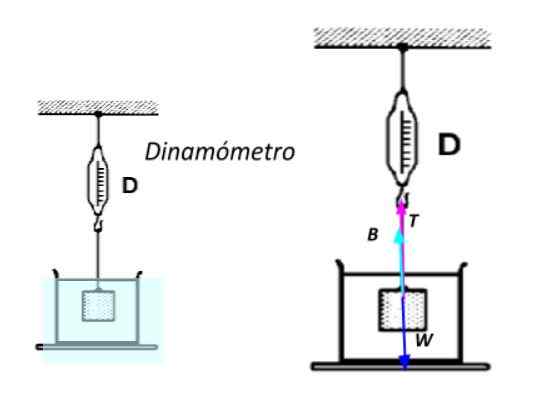Berat badan objek yang tenggelam. Sumber: Disediakan oleh f. Zapata.

Memohon undang -undang kedua Newton mengetahui bahawa objek itu berehat:

Σf_dan = B + t - w = 0

Berat badan yang jelas w_ke Ia bersamaan dengan ketegangan pada tali t:

T = w_ke

W_ke = mg - ρ_fasih . V. g

Jika volum V yang tenggelam diperlukan, ia dibersihkan sebagai:

V = (w - w_ke ) / ρ_fasih  . g

Demonstrasi

https: // giphy.com/gifs/mcphppgtnpbhl4cgaq

Apabila badan merendam, teras adalah daya yang terhasil daripada semua daya yang dikenakan ke atas badan melalui tekanan yang disebabkan oleh cecair sekitarnya:

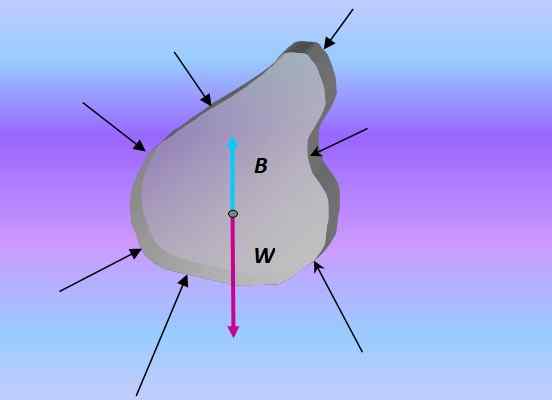Rajah badan percuma objek tenggelam. Sumber: Disediakan oleh f. Zapata.

Tekanan dan kedalaman

Oleh kerana tekanan meningkat dengan kedalaman, hasil daya ini sentiasa diarahkan secara menegak. Oleh itu, prinsip Archimedes adalah akibat dari teorem asas hidrostatik, yang mengaitkan tekanan p yang dikenakan oleh cecair dengan kedalaman z sebagai:

P = ρ.g.z

Memaksa cecair keseimbangan statik

Untuk menunjukkan prinsip Archimedes, bahagian berehat silinder kecil diambil pada rehat untuk menganalisis daya yang dikenakan ke atasnya, seperti yang ditunjukkan dalam angka berikut. Daya di permukaan melengkung silinder dibatalkan antara satu sama lain. 

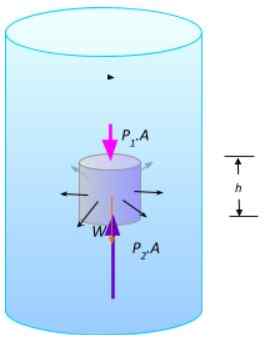Sebahagian cecair dalam keseimbangan. Sumber: Disediakan oleh f. Zapata.

Magnitud daya menegak adalah F₁ = P₁.A dan F₂ = P2.A, ada berat badan W. Oleh kerana bendalir seimbang, jumlah kuasa mesti dibatalkan:

Σf_dan = P₂.A- p₁.A- w = 0

P₂.A- p₁.A = w

Oleh kerana tujahan mengimbangi berat badan, kerana bahagian bendalir sedang berehat, maka:

B = p₂.A- p₁.A = w

Dari ungkapan ini, teraskan bahawa tujahan adalah disebabkan oleh perbezaan tekanan antara muka atas silinder dan lebih rendah. Sebagai W = mg = ρfasih. V. g, Kamu perlu:

B = ρ_fasih. V_tenggelam. g

Yang tepatnya ungkapan untuk tujahan yang disebutkan di bahagian sebelumnya.

Archimedes Prinsip Aplikasi

Belon yang Terapung: Archimedes Prinsip dalam Tindakan

Prinsip Archimedes muncul dalam banyak aplikasi praktikal, antaranya kita boleh namakan:

- Belon aerostatik. Yang dengan mempunyai kepadatan purata kurang daripada udara sekitarnya, terapung di dalamnya kerana daya tujah.

- Kapal. Helmet kapal lebih berat dari air. Tetapi jika badan kapal dianggap ditambah udara di dalam, kuota antara jumlah jisim dan jumlahnya kurang daripada air dan itulah sebabnya mengapa kapal terapung.

- Jaket hidup. Apabila dibina daripada bahan cahaya dan berliang, mereka dapat terapung kerana nisbah jisim massa kurang daripada air.

- Terapung untuk menutup paip pengisian tangki air. Ia adalah sfera yang penuh dengan udara jumlah besar yang mengapung di atas air, yang menyebabkan daya tujahan - didarabkan oleh kesan tuil - menutup topi pengisian tangki air apabila ia mencapai tahap jumlah.

Ia boleh melayani anda: Gelombang Unidimensional: Ekspresi Matematik dan Contoh

Contoh

Contoh 1

Legenda itu mengatakan bahawa Raja Hierón memberikan Goldsmith sejumlah emas untuk membuat mahkota, tetapi raja yang tidak percaya itu berpendapat bahawa tukang emas itu dapat ditipu ketika meletakkan logam yang kurang berharga di dalam mahkota daripada mahkota. Tetapi bagaimana saya boleh tahu tanpa memusnahkan mahkota? 

Raja menugaskan Archimedes dan ini, mencari penyelesaiannya, menemui prinsipnya yang terkenal.

Katakan mahkota beratnya 2.10 kg-f di udara dan 1.95 kg-f ketika tenggelam sepenuhnya di dalam air. Dalam kes ini, tidak ada penipuan?

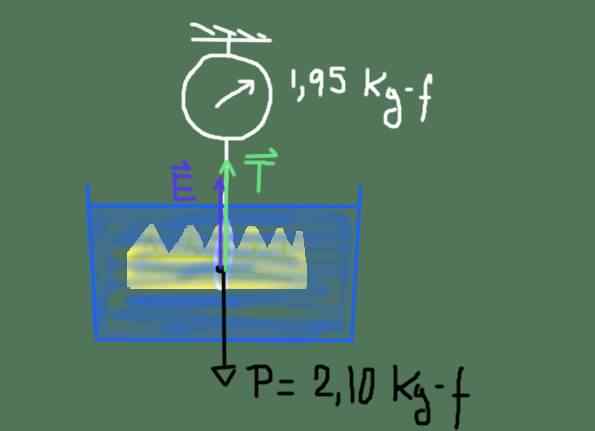Rajah Badan Percuma Mahkota King Heron. Sumber: Disediakan oleh f. Zapata

Gambar rajah daya ditunjukkan dalam angka sebelumnya. Daya ini adalah: berat badan P mahkota, teras Dan dan ketegangan T tali yang tergantung dari skala.

P = 2.10 kg-f dan t = 1.95 kg-f diketahui, perlu menentukan magnitud teras Dan:

T + e = p ⇒ e = p - t = (2.10 - 1.95) kg -f = 0.15 kg -f

Sebaliknya, menurut prinsip Archimedes, teras bersamaan dengan berat air yang diusir ruang yang diduduki oleh mahkota, iaitu kepadatan air dengan jumlah mahkota kerana pecutan graviti :

E = ρ_air⋅V ⋅G = 1000 kg/m^3 ⋅ v ⋅ 9.8m/s^2 = 0.15 kg ⋅ 9.8 m/s^2

Di mana jumlah mahkota boleh dikira:

V = 0.15 kg / 1000 kg / m^3 = 0.00015 m^3

Ketumpatan mahkota adalah kuota antara jisim mahkota keluar dari air dan jumlahnya:

Ketumpatan mahkota = 2.10 kg / 0.00015 m^3 = 14000 kg / m^3

Ketumpatan emas tulen dapat ditentukan oleh prosedur yang sama dan hasilnya ialah 19300 kg/m^3.

Membandingkan dua kepadatan itu jelas bahawa mahkota bukan emas murni! 

Contoh 2 

Berdasarkan data dan hasil dari Contoh 1, adalah mungkin untuk menentukan berapa banyak emas yang dicuri oleh tukang emas dalam kes yang sebahagian emas telah digantikan oleh perak, yang mempunyai ketumpatan 10500 kg/m^3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3.

Kami akan memanggil ρc ke ketumpatan mahkota, ρo ke ketumpatan emas dan ρ_p hingga ketumpatan perak.

Jumlah jisim mahkota adalah:

M = ρc ⋅ v = ρo ⋅ vot + ρ_p⋅ vp

Jumlah jumlah mahkota adalah jumlah perak ditambah jumlah emas:

V = vo + vp ⇒ vp = v - vo

Menggantikan Persamaan Massa:

ρc ⋅V = ρo ⋅ vo + ρ_p⋅ (v - vo) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_p) V

Maksudnya bahawa jumlah emas yang mengandungi mahkota jumlah visian V ialah:

Vo = v ⋅ (ρc - ρ_p)/(ρo - ρ_p) = ..

... = 0.00015 m^3 (14000 - 10500)/(19300 - 10500) = 0.0000596 m^3

Untuk mengetahui berat badan emas yang mengandungi mahkota, kami membiak vo untuk ketumpatan emas:

Boleh melayani anda: peraturan tangan kanan

MO = 19300 *0.00005966 = 1,1514 kg

Oleh kerana jisim mahkota adalah 2.10 kg, kita tahu bahawa 0.94858 kg emas dicuri oleh tukang emas dan digantikan oleh perak.

Latihan yang diselesaikan

Latihan 1

Belon helium besar dapat bertahan seimbang (tanpa naik atau turun) kepada seseorang.

Anggapkan bahawa berat orang itu, ditambah bakul, tali dan belon adalah 70 kg. Berapakah jumlah helium yang diperlukan untuk ini berlaku? Berapa saiz yang akan dimiliki belon?

Penyelesaian

Kami akan mengandaikan bahawa teras dihasilkan terutamanya oleh jumlah helium dan bahawa tujahan seluruh komponennya sangat kecil berbanding dengan helium yang menduduki lebih banyak jumlahnya.

Dalam kes ini, jumlah helium akan diperlukan untuk menyediakan tujahan berat 70 kg +.

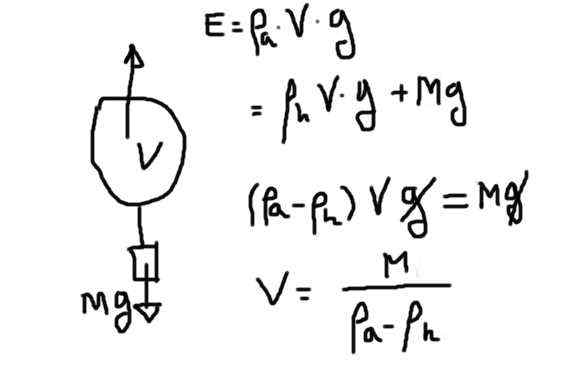Fdiaogram badan percuma penuh dengan helium. Sumber: Disediakan oleh f. Zapata.

Tujahan adalah hasil daripada jumlah helium kerana ketumpatan helium disebabkan oleh pecutan graviti. Teras itu mesti mengimbangi berat helium ditambah berat yang lain.

DA

di mana ia menyimpulkan bahawa v = m / (da - dh)

V = 70 kg / (1.25 - 0.18) kg/m^3 = 65.4 m^3

Iaitu, 65 diperlukan.4 m^3 helium pada tekanan atmosfera untuk sokongan.

Jika kita menganggap belon sfera kita dapat mencari jejari yang sama dari hubungan antara kelantangan dan jejari sfera:

V = (4/3) ⋅ π ⋅ r^3

Di mana r = 2.49 m. Dengan kata lain, diameter 5 m penuh helium diperlukan.

Latihan 2

Bahan ketumpatan yang lebih rendah sehingga air terapung. Anggapkan bahawa anda mempunyai kiub polistirena (gabus putih), kayu dan ais. Ketumpatannya dalam kg setiap meter padu masing -masing: 20, 450 dan 915.

Cari pecahan jumlah jumlahnya keluar dari air dan ketinggian apa yang menonjol berkenaan dengan permukaan air sebagai ketumpatan 1000 kilogram yang terakhir setiap meter padu.

Penyelesaian 

Floatability berlaku apabila berat badan sama dengan tujahan kerana air:

E = m ⋅g

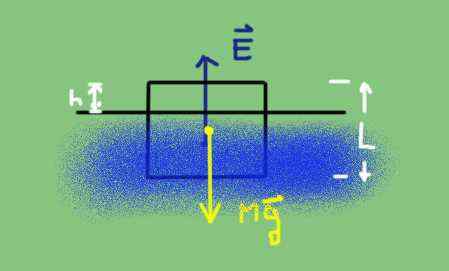Rajah badan percuma objek yang tenggelam sebahagiannya. Sumber: Disediakan oleh f. Zapata.

Berat adalah ketumpatan badan DC didarabkan dengan kelantangan V dan dengan pecutan graviti g.

Tujahan adalah berat cecair yang dipindahkan mengikut prinsip Archimedes dan dikira dengan mengalikan ketumpatan D air oleh volum tenggelam V 'dan dengan pecutan graviti.

Itu dia:

D ⋅ v'⋅g = dc ⋅ vv ⋅g

Yang bermaksud bahawa pecahan kelantangan tenggelam adalah sama dengan kota antara ketumpatan badan dan ketumpatan air.

(V '/v) = (dc/d) 

Iaitu pecahan volume yang luar biasa (v "/v) adalah

(V "/v) = 1 - (dc/d)

Yeah h Ia adalah ketinggian yang luar biasa dan L Sisi kubus pecahan kelantangan boleh ditulis sebagai

(H ⋅l^2)/(l^3) = h/l, Dengan kata lain, pecahan ketinggian yang luar biasa juga

(h/l) = 1 - (dc/d)

Maka hasil untuk bahan yang diminta adalah:

Polystyrene (gabus putih):

(H/l) = (v "/v) = 1 - (dc/d) = 1- (20/1000) = 98% keluar dari air

Kayu:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (450/1000) = 55% keluar dari air

Ais:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (915/1000) = 8.5% keluar dari air

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Mekanik cecair. Asas dan aplikasi. Edisi pertama. McGraw Hill.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 4. Cecair dan termodinamik. Diedit oleh Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Mekanik cecair dan hidraulik. McGraw Hill. 
5. Rex, a. 2011. Asas Fizik. Pearson. 239-263.
6. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. McGraw Hill.