Prisma heksagon

Kami menerangkan apa prisma heksagon, ciri -ciri, elemen, kawasan, simpang, tepi dan bagaimana mengira mereka.

Apa itu prisma heksagon?

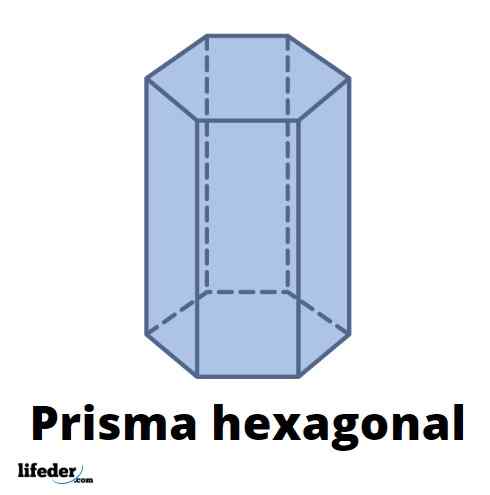
A Prisma heksagon Ia adalah badan tiga dimensi yang terdiri daripada dua bentuk segi enam dan sisi berbentuk seperti segi empat tepat atau parallelogram. Ia boleh didapati dalam alam semula jadi, dalam struktur kristal mineral seperti berilium, grafit, zink dan litium, sebagai contoh.

Unsur -unsur prisma heksagon adalah pangkalan, wajah, tepi, ketinggian, puncak, radio dan apothem. Dari mereka, anda boleh mengira kawasan dan jilid.

Angka atas menunjukkan prisma heksagon dengan wajah segi empat tepat; iaitu, Prisma heksagon lurus. Heksagon pangkalan adalah biasa, iaitu, sisi dan sudut dalaman mereka adalah sama. Walau bagaimanapun, wajah prisma heksagon boleh menjadi heksagon yang tidak teratur.

Ciri -ciri prisma heksagon

1- Hexagonal Prism adalah angka tiga dimensi dengan pangkalan heksagon.

2- Terdapat pelbagai objek yang bertindak balas terhadap definisi ini tetapi mereka agak berbeza.

Dalam angka berikut terdapat pelbagai prisma heksagon: di sebelah kiri prisma heksagon lurus wajah biasa, di sebelah kanan dan ke bawah dua prisma heksagon yang tidak teratur. Heksagon di dasar prisma di bawah mempunyai kekhususan: itu adalah cekung, Yang bermaksud bahawa beberapa sudut dalamannya lebih besar daripada 180 °.

Pelbagai prisma heksagon. Sumber: Wikimedia Commons.

Sebaliknya, asas heksagon prisma di atas adalah poligon cembung: Semua sudut dalaman mengukur kurang daripada 180 °.

Unsur -unsur prisma heksagon

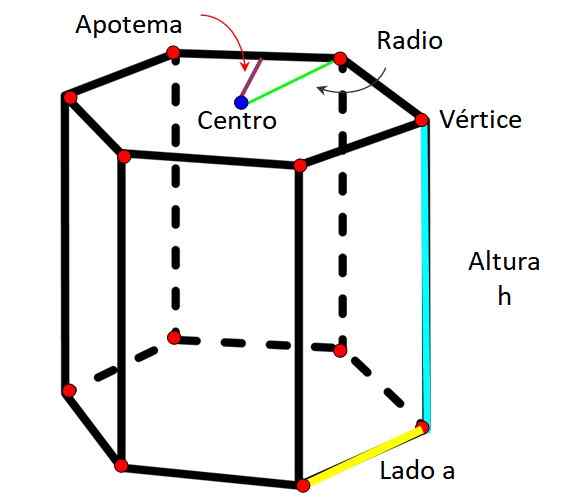Unsur -unsur prisma heksagon. Sumber: f. Zapata

Seperti setiap prisma, prisma heksagon dicirikan dengan mempunyai unsur -unsur berikut:

Boleh melayani anda: songsang berbilang: penjelasan, contoh, latihan yang diselesaikan

-Pangkalan: dalam bilangan dua (2), dalam bentuk heksagon dan kongruen, iaitu ukuran yang sama. Wajah heksagon boleh menjadi biasa atau tidak teratur.

-Muka: Prisma heksagon mempunyai lapan (8) wajah secara total, yang boleh dikira menggunakan Rajah 1. Dari 8 muka, dua (2) adalah pangkalan dan enam (6) adalah sisi.

-Hujung: Ia adalah segmen yang bergabung dengan dua pangkalan atau dua sisi Prisma.

-Ketinggian: Ia adalah jarak antara kedua -dua wajah prisma. Bertepatan dengan panjang tepi dalam kes prisma lurus.

-Puncak: Titik umum antara pangkalan dan dua sisi.

Sekiranya asas prisma adalah biasa, simetri angka ini membolehkan untuk menentukan unsur -unsur tambahan di sisi heksagon biasa ke.

-Radio: Ia adalah jarak yang diukur dari pusat segi enam dan mana -mana puncak.

-Apothem: Ia adalah segmen yang keluar dari pusat wajah heksagon ke tengah satu sisi.

Dengan bantuan unsur -unsur ini, kawasan dan jumlah dikira, seperti yang akan kita lihat kemudian.

Formula

Terdapat banyak formula yang berkaitan dengan prisma heksagon. Mereka berkhidmat untuk mengira kawasan pangkalan dan wajah mereka, jumlahnya dan ciri -ciri pentingnya yang lain. Bidang segi enam biasa, segi enam dan paralelogram yang tidak teratur, serta perimeter, berguna.

Perimeter angka rata

Ia adalah ukuran konturnya, yang dalam hal poligon seperti segi enam adalah jumlah sisinya. Sekiranya Hexagon biasa ke sisi ke, Terdapat formula untuk perimeter P:

P = 6.ke

Kawasan heksagon biasa

Mari panggil Als dan l_Ke Pada panjang apotheme. Kawasan ini diberikan oleh:

Boleh melayani anda: Data yang tidak berkumpul: Contoh dan Latihan Diselesaikan

A = p. L_Ke/2 = 6a. L_Ke/2

Di mana P adalah perimeter angka.

Bergantung pada saiz sisi ke, Kawasan ini juga boleh dikira oleh:

A = 2.5981.ke²

Kawasan heksagon yang tidak teratur

Tidak ada formula khusus, kerana ia bergantung pada susunan sisi, tetapi segi enam dapat dibahagikan kepada segitiga, mengira kawasan masing -masing dan tambahkannya.

Kaedah lain untuk mencari kawasan ini ialah penentu Gauss, yang mana perlu mengetahui koordinat simpang heksagon.

Kawasan Parallelogram

A = BASE X Ketinggian

Yeah ke adalah asas dan h Ia adalah ketinggian, kawasannya adalah:

A = a.h

Kawasan prisma heksagon

Ia adalah jumlah kawasan pangkalan -dua heksagon -dan dari wajah -6 segi empat tepat atau paralelogram-.

Kawasan prisma heksagon biasa

Jika prisma heksagon mempunyai pangkalan dalam bentuk heksagon biasa dan tepi sisi berserenjang dengan pangkalan ini, kawasannya diberikan oleh jumlah:

A = 2 x 2.5981.ke² + 6th.h

Di mana ke Ia adalah sisi segi enam dan h Ia adalah ketinggian prisma.

Kawasan prisma heksagon yang tidak teratur dan lurus

Jika pangkalan adalah heksagon yang tidak teratur, kawasan ini dikira oleh:

A = 2A_asas  + P.h

Di mana:

-Ke_asas Ia adalah kawasan asas heksagon yang tidak teratur.

-P adalah perimeter pangkalan.

-H adalah ketinggian prisma

Simpang

Setiap wajah heksagon mempunyai 6 sudut atau simpul, yang memberikan sejumlah 12 simpul untuk prisma heksagon.

Tepi

Terdapat formula untuk mencari bilangan tepi prisma. Ia ditemui oleh ahli matematik yang hebat Leonhard Euler (1707-1783) dan dipanggil Teorem Euler untuk Polyhedros. Mengatakan demikian:

Boleh melayani anda: Penaakulan algebra

Sekiranya C adalah bilangan muka, dan jumlah vértices V dan jumlah tepi. Memang benar bahawa:

C+v = a+2

Jumlah prisma heksagon adalah: c = 8 dan v = 12. Oleh itu a adalah:

A = C + V - 2 = 8 + 12-2 = 18

Kelantangan

Jumlah V dari mana -mana prisma, sama ada lurus atau serong, wajah biasa atau tidak teratur, diberikan oleh:

V = kawasan asas x ketinggian

Oleh itu, kita memerlukan formula untuk kawasan yang kita lihat sebelumnya.

Sebagai contoh, untuk prisma heksagon lurus, yang asasnya adalah heksagon biasa, jumlahnya diberikan oleh:

V = 2.5981.ke².h

Rujukan

1. Rujukan terbuka matematik. Kawasan Poligon. Pulih dari: Mathpenref.com.
2. Wikipedia. Prisma. Pulih dari: Adakah.Wikipedia.com.