Jumlah harta bersekutu, pendaraban, contoh, latihan

The harta bersekutu jumlahnya mewakili sifat bersekutu operasi menambah dalam pelbagai set matematik. Ia mengaitkan tiga (atau lebih) elemen set ini, yang dipanggil A, B dan C, supaya ia sentiasa dipenuhi:

a + (b + c) = (a + b) + c

Dengan cara ini, dijamin bahawa, tanpa mengira cara kumpulan untuk menjalankan operasi, hasilnya adalah sama.

Rajah 1. Kami menggunakan harta bersekutu jumlahnya berkali -kali ketika melakukan operasi aritmetik dan algebra. (Lukisan: Komposisi Freepik: F. Zapata)

Tetapi harus diperhatikan bahawa harta bersekutu tidak sinonim dengan harta komutatif. Iaitu, kita tahu bahawa urutan tambahan tidak mengubah jumlah atau bahawa urutan faktor tidak mengubah produk. Jadi untuk jumlah yang anda boleh tulis seperti ini: a + b = b + a.

Walau bagaimanapun, di dalam harta bersekutu ia berbeza, kerana perintah unsur -unsur yang akan ditambah dikekalkan dan perubahan apakah operasi yang dilaksanakan terlebih dahulu. Yang bermaksud bahawa ia tidak penting terlebih dahulu (b+c) dan hasil ini menambah, untuk mula menambah b dan hasil tambah c.

Banyak operasi penting seperti jumlahnya adalah bersekutu, tetapi tidak semua. Contohnya dalam pengurangan nombor sebenar ia berlaku:

A - (b - c) ≠ (a - b) - c

Ya A = 2, b = 3, c = 1, kemudian:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Harta pendaraban bersekutu

Seperti yang telah dilakukan untuk jumlah itu, harta bersekutu pendaraban menunjukkan bahawa:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Boleh melayani anda: jumlah polinomial, seperti yang dilakukan, contoh, latihan

Dalam kes set nombor sebenar, mudah untuk mengesahkan bahawa ia selalu. Sebagai contoh, menggunakan nilai a = 2, b = 3, c = 1, anda perlu:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Nombor sebenar memenuhi harta bersekutu dari jumlah dan pendaraban. Sebaliknya, dalam set lain, seperti vektor, jumlahnya bersekutu, tetapi produk silang atau produk vektor tidak.

Aplikasi harta pendaraban bersekutu

Kelebihan bahawa operasi di mana harta bersekutu dipenuhi adalah berkumpulan dengan cara yang paling mudah dipenuhi. Ini sangat memudahkan resolusi.

Contohnya, katakan bahawa di perpustakaan kecil terdapat 3 rak dengan 5 hiburan masing -masing. Dalam setiap hiburan terdapat 8 buku. Berapa banyak buku?

Kita boleh melakukan operasi seperti berikut: jumlah buku = (3 x 5) x 8 = 15 x 8 = 120 buku.

Atau sebagainya: 3 x (5 x 8) = 3 x 40 = 120 buku.

Rajah 2. Permohonan harta pendaraban bersekutu adalah untuk mengira bilangan buku di setiap rak. Imej yang dibuat oleh f. Zapata.

Contoh

-Dalam set nombor semulajadi, keseluruhan, rasional, nyata dan kompleks, harta bersekutu jumlah dan pendaraban dipenuhi.

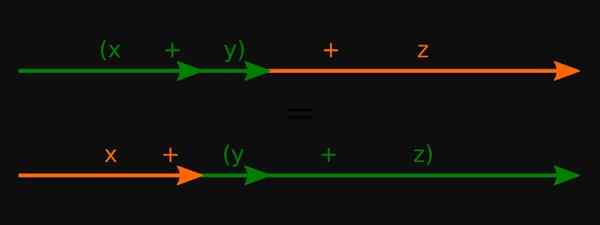Rajah 3. Untuk nombor sebenar, harta bersekutu jumlahnya dipenuhi. Sumber: Wikimedia Commons.

-Untuk polinomial mereka juga memohon dalam operasi ini.

-Dalam kes -kes operasi penolakan, pembahagian dan eksponensi, harta bersekutu tidak dipenuhi dalam bilangan sebenar atau polinomial.

Boleh melayani anda: Orthoedro: formula, kawasan, kelantangan, pepenjuru, contoh

-Dalam kes matriks, harta bersekutu dipenuhi untuk jumlah dan pendaraban, walaupun dalam kes yang kedua, komutiviti tidak dipenuhi. Ini bermakna, diberikan matriks A, B dan C, memang benar bahawa:

(A x b) x c = a x (b x c)

Tetapi ... a x b ≠ b x a

Harta bersekutu dalam vektor

Vektor membentuk set yang berbeza daripada nombor sebenar atau nombor kompleks. Operasi yang ditakrifkan untuk set vektor agak berbeza: terdapat jumlah, penolakan dan tiga jenis produk.

Jumlah vektor memenuhi harta bersekutu, serta nombor, polinomial dan matriks. Bagi produk skalar, memanjat oleh vektor dan salib yang dibuat di antara vektor, yang terakhir tidak memenuhi, tetapi produk skalar, yang merupakan satu lagi jenis operasi antara vektor, memenuhinya, dengan mengambil kira perkara berikut:

-Produk skalar untuk menghasilkan vektor dalam vektor.

-Dan dengan memanjat dua vektor, ia adalah skalar.

Oleh itu, diberi vektor v, atau dan W, Dan tambahan skalar λ, adalah mungkin untuk menulis:

-Jumlah vektor: v +(atau + W ) = (v + atau) + W

-Produk skalar: λ (v • atau ) = (λv) • atau

Yang terakhir mungkin terima kasih kepada apa v • atau Ia adalah skalar, dan λv Ia adalah vektor.

Walau bagaimanapun:

v × (atau × W ) ≠ (v × atau)×W

Pemfaktoran polinomial dengan mengumpulkan istilah

Aplikasi ini sangat menarik, kerana seperti yang dinyatakan di atas, harta bersekutu membantu menyelesaikan masalah tertentu. Jumlah monomial adalah bersekutu dan ini dapat digunakan untuk faktor apabila faktor umum yang jelas tidak muncul pada pandangan pertama.

Boleh melayani anda: cembung poligon: definisi, elemen, sifat, contoh

Sebagai contoh, katakan ia diminta untuk faktor: x³ + 2x² + 3x +6. Polinomial ini tidak mempunyai faktor yang sama, tetapi mari kita lihat apa yang berlaku jika ia dikelompokkan dengan cara ini:

x³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Kurungan pertama mempunyai faktor biasa x²:

x³ + 2x² = x² (x+2)

Pada yang kedua faktor umum ialah 3:

3x +6 = 3 (x + 2)

Jadi:

x³ + 2x² + 3x +6 = x²(x+ 2)+ 3 (x+ 2)

Sekarang ada faktor umum yang jelas, iaitu x+2:

x²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Latihan

- Latihan 1

Bangunan sebuah sekolah mempunyai 4 tingkat dan di setiap kelas terdapat 12 bilik darjah dengan 30 meja di dalamnya. Berapa banyak meja yang dimiliki oleh sekolah?

Penyelesaian

Masalah ini diselesaikan dengan menggunakan harta pendaraban bersekutu, mari kita lihat:

Jumlah meja = 4 tingkat x 12 bilik darjah /lantai x 30 meja /kelas = (4 x 12) x 30 meja = 48 x 30 = 1440 meja.

O Jika disukai: 4 x (12 x 30) = 4 x 360 = 1440 meja

- Latihan 2

Memandangkan polinomial:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Sapukan harta bersekutu dari jumlah untuk mencari (x) + b (x) + c (x).

Penyelesaian

Dua yang pertama boleh dikelompokkan dan hasilnya menambah yang ketiga:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polinomial c (x) segera ditambah:

[x⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Pembaca boleh mengesahkan bahawa hasilnya sama jika diselesaikan dengan pilihan A (x) + [b (x) + c (x)]].

Rujukan

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Matematik menyeronokkan. Undang -undang komutatif, bersekutu dan daerah. Pulih dari: Mathisfun.com.
3. Gudang Matematik. Definisi harta bersekutu. Pulih dari: Mathwarehouse.com.
4. Saintifik. Harta bersekutu & komutatif tambahan & pendaraban (dengan contoh). Pulih dari: saintifik.com.
5. Wikipedia. Harta bersekutu. Diperoleh dari: dalam.Wikipedia.org.