Bukti Harta Harta, Contohnya

The Algebra Lock Property Ia adalah fenomena yang mengaitkan dua elemen set dengan operasi, di mana keadaan yang diperlukan adalah, selepas 2 elemen di bawah operasi tersebut, hasilnya juga milik set awal.

Contoh. Ini kerana jumlah 2 nombor bahkan akan selalu diberikan hasilnya nombor lain, dengan itu memenuhi syarat kunci.

Sumber: Unspash.com

[TOC]

Ciri -ciri

Terdapat banyak sifat yang menentukan ruang atau badan algebra, seperti struktur atau cincin. Walau bagaimanapun, harta kunci adalah salah satu yang paling terkenal dalam aljabar asas.

Tidak semua aplikasi sifat -sifat ini berdasarkan fenomena atau elemen berangka. Banyak contoh sehari-hari dapat berfungsi dari pendekatan algebra-teoretikal murni.

Contohnya boleh menjadi warganegara negara yang menganggap hubungan undang -undang dalam apa jua bentuk, seperti masyarakat komersial atau perkahwinan antara lain. Selepas operasi atau pengurusan ini, mereka masih menjadi warganegara negara. Oleh itu, operasi kewarganegaraan dan pengurusan berkenaan dengan dua warganegara mewakili kunci.

Algebra berangka

Berkenaan dengan nombor, terdapat banyak aspek yang telah menjadi alasan untuk belajar dalam arus matematik dan algebra yang berlainan. Dari kajian ini, sejumlah besar aksioma dan teorem telah muncul sebagai asas teori penyelidikan dan kerja kontemporari.

Sekiranya anda bekerja dengan set berangka, kami dapat menetapkan definisi lain yang sah untuk harta kunci. Dikatakan bahawa satu set A adalah kunci set lain B jika A adalah set terkecil yang mengandungi semua set dan operasi yang rumah b.

Boleh melayani anda: harta pengedaran

Demonstrasi

Demonstrasi kunci digunakan untuk elemen dan operasi yang terdapat dalam set nombor N sebenar.

Biarkan A dan B menjadi dua nombor yang dimiliki oleh set r, kunci unsur -unsur ini ditakrifkan untuk setiap operasi yang terkandung dalam r.

Tambahan

- Jumlah: ∀ A ˄ B ∈ R → A + B = C ∈ R

Ini adalah cara algebra untuk mengatakannya Untuk semua A dan B yang dimiliki oleh nombor sebenar, ia harus menjadi jumlah B lebih sama dengan C, yang juga dimiliki oleh sebenar.

Adalah mudah untuk memeriksa sama ada cadangan ini adalah benar; Sudah cukup untuk membuat jumlah antara nombor sebenar dan sahkan jika hasilnya juga dimiliki oleh nombor sebenar.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Diperhatikan bahawa keadaan kunci dipenuhi untuk nombor sebenar dan jumlahnya. Dengan cara ini dapat disimpulkan: Jumlah nombor sebenar adalah kunci algebra.

Pendaraban

- Pendaraban: ∀ ˄ b ∈ R → a . B = c ∈ R

Untuk semua A dan B yang dimiliki oleh yang sebenar, pendaraban A untuk B sama dengan C, yang juga dimiliki oleh sebenar.

Apabila mengesahkan dengan elemen yang sama dari contoh sebelumnya, hasil berikut diperhatikan.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Ini adalah bukti yang mencukupi untuk menyimpulkan bahawa: Pendaraban nombor sebenar adalah kunci algebra.

Definisi ini dapat diperluaskan kepada semua operasi nombor nyata, walaupun kita akan menemui pengecualian tertentu.

Sumber: Pixabay.com

Kes Khas dalam R

Bahagian

Sebagai kes khas, bahagian ini diperhatikan, di mana pengecualian berikut dihargai:

Boleh melayani anda: kebarangkalian klasik: pengiraan, contoh, latihan yang diselesaikan

∀ A ˄ b ∈ R → A / B ∉ R ↔ B = 0

Untuk semua a dan b yang milik R Ia mesti antara B tidak tergolong dalam reais jika dan hanya jika b adalah sama dengan sifar.

Kes ini merujuk kepada sekatan tidak dapat membahagikan antara sifar. Kerana sifar tergolong dalam nombor sebenar, maka disimpulkan bahawa: LBahagian bukan kunci yang sebenarnya.

Radio

Terdapat juga operasi potentiasi, lebih khusus yang memfailkan, di mana pengecualian dibentangkan untuk kuasa radikal indeks tork:

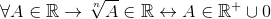; Dengan n par

Untuk semua yang dimiliki oleh Royal.

Dengan cara ini ia dilambangkan bahawa akar walaupun hanya berlaku kepada yang sebenar yang positif dan disimpulkan bahawa potentiation bukan kunci dalam r r.

Logaritma

Ia diluluskan untuk fungsi logaritma, yang tidak ditakrifkan untuk nilai yang lebih kecil atau sama dengan sifar. Untuk memeriksa sama ada logaritma adalah hasil kunci R seperti berikut:

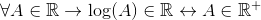
Untuk segala -galanya yang dimiliki oleh Reais, logaritma A adalah milik reais, jika dan hanya jika ia milik positif yang positif.

Apabila nilai negatif dan sifar yang juga tergolong dalam R dikecualikan, ia boleh disahkan bahawa:

Logaritma bukan kunci nombor sebenar.

Contoh

Semak kunci untuk jumlah dan penolakan nombor semula jadi:

Jumlah dalam n

Perkara pertama adalah untuk memeriksa keadaan kunci untuk unsur -unsur yang berbeza dari set yang diberikan, di mana jika diperhatikan bahawa beberapa elemen pecah dengan keadaan, kewujudan kunci dapat ditolak secara automatik.

Boleh melayani anda: Radio konvergensi: definisi, contoh dan latihan yang diselesaikan

Harta ini dipenuhi untuk semua kemungkinan nilai A dan B, seperti yang diperhatikan dalam operasi berikut:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Tidak ada nilai semula jadi yang memecahkan keadaan kunci, jadi disimpulkan:

Jumlahnya adalah kunci dalam n.

Tolak dalam n

Unsur -unsur semulajadi dicari mampu melanggar keadaan; A - b milik orang asli.

Beroperasi adalah mudah untuk mencari pasangan unsur semula jadi yang tidak memenuhi syarat kunci. Sebagai contoh:

7 - 10 = -3 ∉ a n

Dengan cara itu kita dapat menyimpulkan bahawa:

Penolakan bukan kunci set nombor semula jadi.

Latihan yang dicadangkan

1-SAMP.

2-dijelaskan jika set nombor sebenar adalah kunci keseluruhan nombor keseluruhan.

3-Keterangan set berangka yang boleh menjadi kunci nombor sebenar.

4-sampel harta kunci untuk set nombor khayalan, berkenaan dengan jumlah, penolakan, pendaraban dan pembahagian.

Rujukan

1. Panorama Matematik Murni: Pilihan Bourbakist. Jean Dieudonné. Reverte, 1987.
2. Teori nombor algebra. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Universiti Autonomi Negara Mexico, 1975.
3. Algebra linear dan aplikasinya. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Struktur Algebra V: Teori Badan. Héctor a. Merklen. Pertubuhan Negara Amerika, Sekretariat Agung, 1979.
5. Pengenalan kepada aljabar komutatif. Michael Francis Atiyah, i. G. MacDonald. Reverte, 1973.