Laman utama
Matematik
Hadkan sifat (dengan contoh)

Matematik

Hadkan sifat (dengan contoh)

The Had sifat Mereka adalah set peraturan dan prosedur algebra yang digunakan untuk menentukannya. Konsep had adalah penting untuk pengiraan dan mencari nilainya tidak perlu menjadi tugas rumit, dengan syarat sifatnya ditangani dengan mudah.

Berikut adalah senarai yang paling penting, disertai dengan contoh aplikasi.

Had dan sifatnya adalah asas pengiraan. Had yang sangat istimewa ditunjukkan dalam Rajah: Derivatif fungsi F (x)

Biarkan b, c, n, a dan b nombor sebenar, dan F dan g Fungsi sedemikian yang mengesahkan perkara berikut:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Kemudian anda mempunyai sifat berikut:

1. Had penggantian langsung

Pada mulanya, had fungsi f apabila x → c dapat dikira secara langsung menggantikan x = c dalam fungsi. Jika fungsi wujud pada x = c, maka hadnya ialah:

$\lim_x \rightarrow c f(x)=f(c)$ Tetapi tidak semestinya fungsi mesti ditakrifkan pada x = c supaya batas ada. Idea ini adalah untuk mendekati seberapa banyak yang anda mahu nilai x = c dan lihat apa yang berlaku dengan fungsi dalam kes itu.

Contoh

Cari had f (x) = x² Bila x → 4

Penyelesaian

Hadnya menyelesaikan dengan menggantikan x = 4 dalam f (x) = x², Oleh kerana tidak ada kesulitan dalam menjalankan operasi:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Keunikan had

Sekiranya had fungsi f (x) apabila x → c wujud dan bernilai l, had tersebut adalah unik.

Oleh itu, had sisi, yang mana ketika x → c^- (Baca "X cenderung ke C dari kiri") dan apabila x → c⁺(Ia berbunyi "X cenderung ke C di sebelah kanan"), kedua -duanya wujud dan mempunyai nilai yang sama l, walaupun fungsi tidak ditakrifkan dalam x = c.

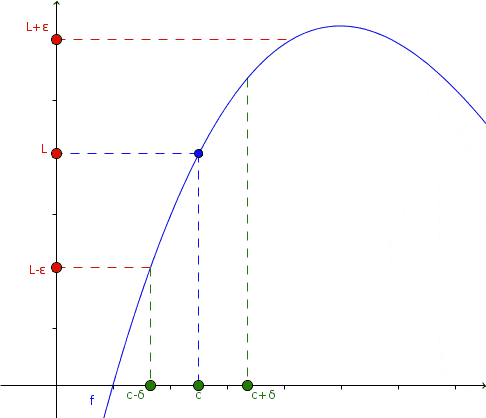Dalam animasi ini konsep had dibentangkan: apabila x cenderung kepada nilai tertentu c, menghampiri kedua -dua kiri dan kanan, nilai fungsi cenderung kepada l. Tidak semestinya fungsi ditakrifkan dalam x = c. Sumber: Wikimedia Commons.

Dalam animasi pendekatan ini diperhatikan dan apa yang berlaku dengan fungsi dalam kes itu: sama ada ia menghampiri di sebelah kiri dan di sebelah kanan ke x = c, nilai fungsi pula adalah dekat dengan l.

Boleh melayani anda: dataran minimum

Secara matematik menyatakan cara ini:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Had sisi membolehkan mengetahui bila had wujud atau tidak, kerana jika mereka tidak wujud atau jika mereka berbeza, pasti bahawa had fungsi apabila x → c tidak wujud.

Contoh

Kirakan had f (x) apabila x → 1 jika wujud, di mana f (x) diberikan oleh:

Penyelesaian

Ini adalah fungsi mengikut bahagian atau ditakrifkan pada kepingan, yang terdiri daripada baris 4 -x untuk nilai x < 1 y en la parábola 4 - x² Apabila x bersamaan dengan 1 atau lebih besar daripada 1.

Kita boleh mendekati x = 1 dari kiri, dalam hal ini bahagian fungsi yang sah untuk x diambil<1:

Oleh kerana had sisi adalah sama, ia mengikuti bahawa had fungsi apabila x → 1 wujud dan bernilai 3.

3. Malar

Had pemalar adalah nilai yang berterusan, tanpa mengira nilai yang mana pembolehubah cenderung:

$\lim_x\rightarrow cb=b .$

Contoh

Kira:

$\lim_x\rightarrow 1\pi$ Penyelesaian

$\lim_x\rightarrow 1\pi= \pi$

4. Had fungsi identiti

Jika f (x) = x, ia sentiasa dipenuhi bahawa:

$\lim_x\rightarrow cx=c$

Contoh

Kira:

$\lim_x\rightarrow 2x$ Penyelesaian

$\lim_x\rightarrow 2x=2$

5. Had produk pemalar dengan fungsi

Dalam kes ini, pemalar keluar dari had dan bergerak untuk membiaknya, seperti ini:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Contoh

Hitung, jika ada, had berikut:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Penyelesaian

Pemalar 5 berada di luar mendarabkan ke had dan harta gantian digunakan:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Had jumlah

Had jumlah dua fungsi F dan g Ia adalah jumlah had:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Contoh

Cari had berikut jika ada:

Boleh melayani anda: Tetapkan Teori: Ciri, Elemen, Contoh, Latihan

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Penyelesaian

Harta jumlah had digunakan terlebih dahulu dan kemudian penggantian langsung, kerana operasi tidak menimbulkan kesukaran:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Had pengurangan

Dalam hal batas pengurangan dua fungsi, teruskan dengan cara yang sama untuk jumlah: had penolakan adalah pengurangan had:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Contoh

Kirakan had berikut:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Penyelesaian

Harta had pengurangan dua fungsi digunakan dan kemudian penggantian langsung, kerana semua operasi dapat dilakukan tanpa masalah:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Had produk

Had produk dua fungsi F dan g Ia adalah produk had:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Contoh

Kirakan had ini:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Penyelesaian

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Nisbah Kota

Had nisbah dua fungsi F dan g Adalah kuota had, dengan syarat bahawa had g (x) apabila x → c berbeza dari 0, kerana pembahagian oleh 0 tidak ditakrifkan. Jadi:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Contoh

Hitung, jika ada, nilai had berikut:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Penyelesaian

Pada mulanya, harta had harta tanah digunakan, untuk mendapatkan kuota had:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Harta gantian kini digunakan untuk mencari setiap had:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

Dan sejak b ≠ 0, had yang dicari adalah kuota a/b:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Had

Batasan kuasa eksponen n, bersamaan dengan had yang dibangkitkan kepada kuasa tersebut, seperti berikut:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Kes 1: Had kuasa x

Jika anda mempunyai, sebagai contoh, had kuasa x, hasilnya:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Menurut harta 4, had ini adalah:

Boleh melayani anda: Analogi berangka: Jenis, Aplikasi dan Latihan

$\lim_x \rightarrow c x^n=c^n$

Kes 2: Had Akar

Akar n-ini boleh ditulis dalam bentuk eksponen pecahan, oleh itu:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Penting: Sekiranya indeks akar adalah, perlu had f (x) apabila x → c lebih besar daripada atau sama dengan 0, kerana tidak ada pasangan sebenar jumlah negatif.

Contoh

Tentukan, memohon sifat -sifat sebelumnya, had berikut jika ia wujud:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Penyelesaian kepada

Dengan harta had kuasa dan penggantian langsung ia diperolehi:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Penyelesaian b

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

sebelas. Had

Untuk mencari had asas eksponen asas b dan eksponen f (x), asas fungsi fungsi f (x) mesti dibangkitkan seperti berikut:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Contoh

Cari jika terdapat had berikut:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Penyelesaian

Dalam had ini asas adalah nombor e dan fungsi f (x) = x², Oleh itu anda perlu mengira had x terlebih dahulu² Apabila X cenderung kepada 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Kemudian harta had eksponen digunakan:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Had fungsi berpotensi eksponen

Had apabila x → c fungsi f (x), yang seterusnya dinaikkan ke fungsi lain g (x) dinyatakan oleh:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Contoh

Kirakan had berikut, jika ada:

$\lim_x \rightarrow -1 (x-1)^^2x$

Penyelesaian

Untuk memohon harta sebelumnya, mereka mula-mula dikenal pasti f (x) = x-1 dan g (x) = 2x dan kemudian had masing-masing dikira:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Akhirnya:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Rujukan

Ayres, f. 2000. Pengiraan. 5ed. MC Graw Hill.
Leithold, l. 1992. Pengiraan dengan geometri analisis. Harla, s.Ke.
Teks matematik percuma. Had. Pulih dari: matematik.Liibretexts.org.
Mathemovil. Undang -undang dan hadkan sifat. Pulih dari: Matemovil.com.
Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
Purcell, e. J., Varberg, d., & Rigdon, s. Dan. (2007). Pengiraan. Mexico: Pendidikan Pearson.
Formula Universe. Had sifat. Pulih dari: universoformulas.com

Hadkan sifat (dengan contoh)

1. Had penggantian langsung

Contoh

Penyelesaian

2. Keunikan had

Contoh

Penyelesaian

3. Malar

Contoh

Penyelesaian

4. Had fungsi identiti

Contoh

Penyelesaian

5. Had produk pemalar dengan fungsi

Contoh

Penyelesaian

6. Had jumlah

Contoh

Penyelesaian

7. Had pengurangan

Contoh

Penyelesaian

8. Had produk

Contoh

Penyelesaian

9. Nisbah Kota

Contoh

Penyelesaian

10. Had

Kes 1: Had kuasa x

Kes 2: Had Akar

Contoh

Penyelesaian kepada

Penyelesaian b

sebelas. Had

Contoh

Penyelesaian

12. Had fungsi berpotensi eksponen

Contoh

Penyelesaian

Rujukan

Artikel Terbaik

Julio Jaramillo Biografi dan Kerja

Julio Jaramillo (1935 - 1978) adalah penyanyi dan pemuzik Ecuador yang terkenal, yang dikenali sebag...

Ciri -ciri dan contoh kandungan prosedural

Kandungan prosedur adalah salah satu daripada tiga jenis kandungan utama yang dapat diajar dalam per...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Keunikan had

$\lim_x\rightarrow 1\pi$ Penyelesaian

$\lim_x\rightarrow 2x$ Penyelesaian

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Contoh

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Penyelesaian

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Penyelesaian

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Penyelesaian

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Contoh

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Penyelesaian

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Kes 1: Had kuasa x

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Penyelesaian

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Rujukan