Apakah reaktansi kapasitif dan bagaimana mengira?

The Reaktansi kapasitif Ia adalah rintangan bahawa kondensor, elemen pengawalseliaan aliran beban dalam litar semasa yang berselang -seli, menentang laluan arus.

Dalam litar yang terdiri daripada pemeluwap dan diaktifkan oleh sumber semasa yang berselang -seli, reaktansi kapasitif x dapat ditakrifkan_C seperti berikut:

X_C = 1 / Ωc

Rajah 1. Reaksi kapasitif adalah sebahagian daripada penapis Passabajos dan penceramah penceramah. Sumber: Pixabay.

Atau juga:

X_C = 1 / 2πfc

Di mana C ialah kapasiti kapasitor dan Ω adalah kekerapan sudut sumber, yang berkaitan dengan kekerapan f melalui:

Ω = 2πf

Reaktansi kapasitif bergantung kepada kebalikan kekerapan, oleh itu pada frekuensi tinggi cenderung kecil, sementara pada frekuensi rendah, reaktansi adalah besar.

Unit sistem antarabangsa untuk mengukur reaktansi kapasitif adalah OHM (Ω), dengan syarat kapasiti kapasitor berada di Farad, (disingkat f) dan kekerapan dinyatakan dalam songsang detik (s^-1).

Walaupun beban berlangsung, voltan dan arus juga ditubuhkan melalui kapasitor, yang amplitud maksimum atau nilai, dilambangkan masing -masing sebagai v_C dan saya_C, Mereka berkaitan dengan reaktansi kapasitif yang sama dengan undang -undang Ohm:

V_C = I_C ⋅ x_C

Dalam pemeluwap, voltan ditangguhkan 90º berkenaan dengan arus, atau ia maju 90º berkenaan dengan itu, seperti yang disukai. Dalam apa jua keadaan kekerapan adalah sama.

Bila x_C Ia sangat besar, arus cenderung kecil dan menjadikan nilai x tak terhingga_C, Pemeluwap berkelakuan seperti litar terbuka dan arus adalah sifar.

[TOC]

Cara mengira reaktansi kapasitif

Mari kita lihat contoh bagaimana untuk mengira reaktansi kapasitif: Katakan kapasitor 6 μF disambungkan ke outlet kuasa dan kekerapan bergantian dan kekerapan F 60 Hz.

Untuk mencari reaksi kapasitif, definisi yang diberikan pada mulanya digunakan. Kekerapan sudut Ω diberikan oleh:

Ia boleh melayani anda: induksi magnet: formula, bagaimana ia dikira dan contohnya

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Maka hasil ini digantikan dalam definisi:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

Sekarang mari kita lihat amplitud semasa beredar di litar. Oleh kerana sumber menawarkan voltan amplitud v_C = 40 V, kita menggunakan hubungan antara reaktansi kapasitif, arus dan voltan untuk mengira amplitud arus maksimum atau arus:

Yo_C = V_C / X_C = 40 V / 442.1 ohm = 0.09047 A = 90.5 m a.

Sekiranya kekerapan menjadi sangat besar, reaktansi kapasitif menjadi kecil, tetapi jika kekerapan menjadi 0 dan kita mempunyai arus langsung, reaktansi akan cenderung tidak terhingga.

Voltan semasa dan kondensor

Apabila pemeluwap menghubungkan ke sumber semasa yang berselang -seli, seperti ia berayun dan mengubah polaritasnya, kapasitor mengalami beban dan pelepasan secara bergantian.

Untuk kekerapan 60 Hz seperti contohnya, voltan positif 60 kali sesaat, dan negatif lain 60 kali sesaat.

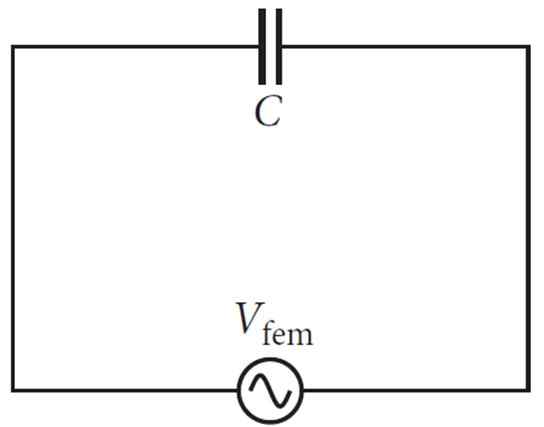
Rajah 2. Litar pemeluwap mudah dan sumber semasa berselang -seli. Sumber: f. Zapata.

Dengan meningkatkan voltan, ia memacu arus dalam satu arah, tetapi jika pemeluwap dimuat turun, arus berlaku ke arah yang bertentangan yang menentang yang pertama.

Ya v_C (t) = v_m Sen ωt, mengetahui bahawa kapasiti adalah sebab antara beban dan voltan, kita akan mempunyai beban:

C = q/v → q (t) = cv = cv_m Sen ωt

Dan mempunyai beban bergantung pada masa, kita akan mempunyai arus, yang merupakan terbitan itu:

Yo_C(t) = cv_m Ω cos ωt

Tetapi payudara dan kosinus berkaitan melalui: cos α = sin (α + π/2), oleh itu:

Yo_C(t) = cv_m Ω sen (ωt + π/2) = i_C Sen (ωt + π/2)

Dengan i_C = Cv_C Ω

Seperti yang dapat dilihat, terdapat perbezaan 90º pendahuluan arus berkenaan dengan voltan, seperti yang dikomentari pada awalnya.

Boleh melayani anda: Eksperimen Millikan: Prosedur, Penjelasan, Kepentingan

Dalam perihalan jenis litar ini, konsep Fasor, yang kelihatan seperti vektor dan membolehkan untuk mewakili dalam satah kompleks sebarang jumlah berganti seperti arus, voltan atau impedans.

Angka berikut menunjukkan, di sebelah kanan, voltan dan fasores semasa dalam kapasitor, yang membentuk sudut 90º, yang merupakan ketinggalan antara kedua -dua.

Di sebelah kiri adalah graf masing -masing, amplitud yang berbeza, tetapi kekerapan yang sama. Pada waktunya, kemajuan semasa ke voltan dan apabila ini maksimum, arus adalah sifar dan apabila voltan adalah sifar, arus adalah maksimum tetapi dengan polaritas terbalik.

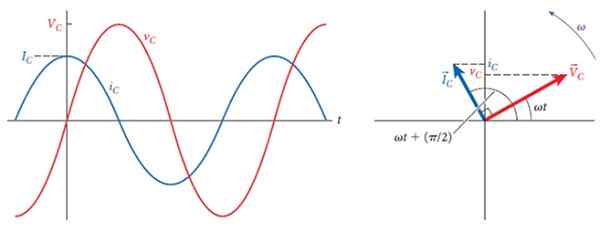Rajah 3. 90º lag antara arus dan voltan melalui kapasitor. Sumber: Bauer, W.

Impedans kondensor kompleks

Dalam litar dengan rintangan, kapasitor dan induktansi, reaksi adalah bahagian khayalan z impedans, jumlah yang kompleks yang dalam litar semasa bergantian mempunyai peranan yang serupa dengan rintangan elektrik untuk arus langsung.

Malah, impedans litar ditakrifkan sebagai sebab antara voltan dan arus:

Z = v / i

Untuk kapasitor atau kapasitor, impedansnya diberikan oleh kuota:

Z_C = v (t) / i (t) = v_C Sen Ωt / i_C Sen (ωt + π/2)

Cara mengekspresikan voltan dan arus sebagai fasores adalah untuk menunjukkan amplitud dan sudut fasa (bentuk kutub):

v (t) = v_C ∠ 0º

I (t) = i_C ∠ 90º

Oleh itu:

Z_C = V_C ∠ 0º / i_C ∠ 90º = (v_C / Yo_C) ∠ 0º -90º =

= V_C / CV_C Ω ◦ -90º = (1/ ωc) ∠ -90º =

Z_C = (- j) x_C

Iaitu, impedans pemeluwap adalah reaktansi kapasitif yang didarabkan oleh negatif unit khayalan.

Impedans litar siri RC

Impedans litar semasa berselang dengan rintangan, kapasitor dan induktor juga boleh diwakili oleh Binomial oleh:

Ia boleh melayani anda: Undang -undang Termodinamik Pertama: Formula, Persamaan, Contoh

Z = r + jx

Dalam persamaan ini, r mewakili rintangan, yang sepadan dengan bahagian sebenar, j ialah unit khayalan dan x adalah reaktansi, yang boleh kapasitif atau induktif atau gabungan kedua -duanya, jika unsur -unsur ini hadir pada masa yang sama di litar.

Jika litar mengandungi rintangan dan kapasitor bersiri, impedansnya adalah:

Z = z_R + Z_C    

Seperti dalam voltan rintangan dan arus dalam fasa, impedans rintangan hanyalah nilai rintangan r r.

Dalam kes impedans kapasitif, kita telah melihat bahawa z_C = -Jx_C , Oleh itu, impedans litar RC adalah:

Z = r - jx_C = R - J (1/ ωc)

Contohnya dalam litar yang ditunjukkan di bawah, sumbernya adalah bentuk:

100 v ⋅ sen (120πt)

Memerhatikan bahawa Ω = 120π, impedans ialah:

Z = 83.0 - J [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 J ohm.

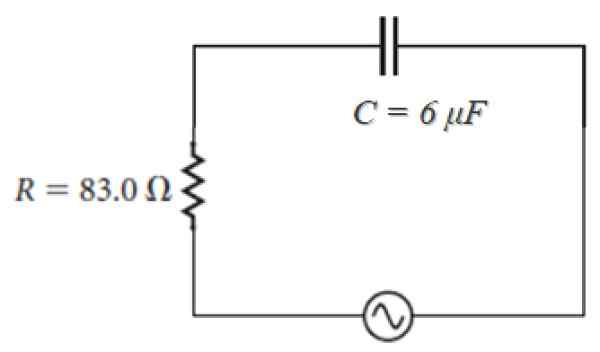Rajah 4. Siri litar RC dengan sumber semasa berselang. Sumber: f. Zapata.

Aplikasi reaktansi kapasitif

Penapis tinggi PASA, penapis lulus rendah, litar jambatan untuk mengukur kapasitans dan induktansi dan litar peti sejuk adalah antara aplikasi litar utama yang mengandungi reaksi kapasitif, digabungkan dengan induktansi dan rintangan elektrik.

Dalam peralatan bunyi, beberapa penceramah datang dengan jenis jenis yang berasingan Woofer (lebih besar) untuk frekuensi rendah dan Tweeter atau tanduk kecil untuk frekuensi tinggi. Dengan cara ini, prestasi dan kualiti audio bertambah baik.

Mereka digunakan kapasitor yang menghalang ketibaan frekuensi rendah di tweeter, manakala induktor ditambah dalam woofer untuk mengelakkan isyarat frekuensi tinggi, kerana induktansi mempunyai reaksi yang berkadar dengan kekerapan: x x_L = 2πfl.

Rujukan

1. Alexander, c. 2006. Asas Litar Elektrik. Ke -3. Edisi. MC Graw Hill.
2. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 2. MC Graw Hill.
3. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
5. Serway, r., Jewett, J. 2008. Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.